Выпуклое программирование
Общая задача выпуклого программирования имеет вид
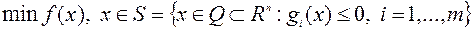 (6.4.1)
(6.4.1)
где 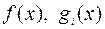 – выпуклые функции,
– выпуклые функции, 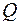 – выпуклое множество.
– выпуклое множество.
Будем обозначать 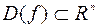 – область определения функции, т.е. множество на котором функция определена, а за его пределами не определена.
– область определения функции, т.е. множество на котором функция определена, а за его пределами не определена.
Условия экстремума. Необходимые и достаточные условия задачи (6.4.1) сформулированы в следующей теореме.
Теорема 17 (Кун-Таккер). Пусть 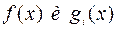 , i=1,…,m, – выпуклые функции,
, i=1,…,m, – выпуклые функции, 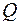 – выпуклое множество, входящее в области определения функций
– выпуклое множество, входящее в области определения функций 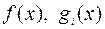 и выполняется условие Слейтера: найдется
и выполняется условие Слейтера: найдется 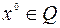 такое, что
такое, что
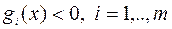 (6.4.2)
(6.4.2)
Тогда допустимая точка 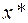 является глобальным решением (6.4.1), если и только если найдутся
является глобальным решением (6.4.1), если и только если найдутся 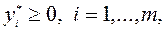 такие, что:
такие, что:
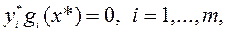 и (6.4.3)
и (6.4.3)
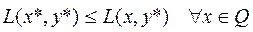 , (6.4.4)
, (6.4.4)
где 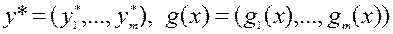 и
и
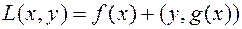 , (6.4.5)
, (6.4.5)
Как и ранее функцию 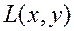 будем называть функцией Лагранжа, вектор
будем называть функцией Лагранжа, вектор 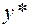 – множителями Лагранжа,
– множителями Лагранжа, 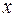 – прямыми переменными,
– прямыми переменными, 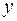 – двойственными переменными, условие
– двойственными переменными, условие 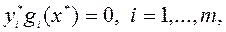 – условием дополняющей нежесткости, набор индексов
– условием дополняющей нежесткости, набор индексов 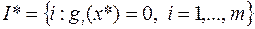 – множеством активных ограничений. Если для задачи (6.4.1) выполнены условия теоремы 1, то будем говорить о регулярной точке минимумаили регулярной задаче.
– множеством активных ограничений. Если для задачи (6.4.1) выполнены условия теоремы 1, то будем говорить о регулярной точке минимумаили регулярной задаче.
Теорема Куна-Таккера утверждает, что в случае регулярной точки минимума 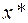 найдутся неотрицательные множители Лагранжа
найдутся неотрицательные множители Лагранжа 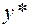 , удовлетворяющие условию дополняющей нежесткости, такие, что функция Лагранжа при
, удовлетворяющие условию дополняющей нежесткости, такие, что функция Лагранжа при 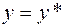 достигает минимума на
достигает минимума на 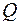 в точке
в точке 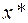 . Таким образом появляется возможность свести задачу с неравенствами к задаче минимизации без ограничений.
. Таким образом появляется возможность свести задачу с неравенствами к задаче минимизации без ограничений.
Пусть 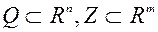 – два множества. Пара
– два множества. Пара 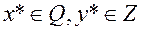 называется седловой точкой функции
называется седловой точкой функции 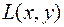 на
на 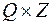 , если
, если
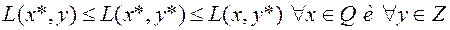 (6.4.6)
(6.4.6)
т.е. точка 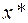 является точкой минимума
является точкой минимума 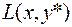 по
по 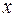 на
на 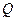 , а
, а 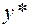 – точкой максимума
– точкой максимума 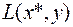 по
по 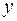 на
на 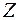 . Выражение (6.4.6) эквивалентно равенству
. Выражение (6.4.6) эквивалентно равенству
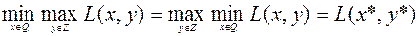 . (6.4.7)
. (6.4.7)
Наличие седловой точки означает возможность перестановки операций минимума и максимума.
Теорема 18 (Кун-Таккер). В условиях теоремы 1 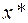 является решением задачи (6.4.1) тогда и только тогда, когда пара
является решением задачи (6.4.1) тогда и только тогда, когда пара 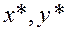 при некотором
при некотором 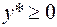 является седловой точкой
является седловой точкой 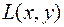 на
на 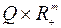 , т.е.
, т.е.
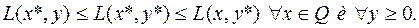 (6.4.8)
(6.4.8)
Двойственность. Симметрия относительно переменных 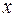 и
и 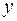 в (6.4.8) для задачи минимизации (6.4.1) по
в (6.4.8) для задачи минимизации (6.4.1) по 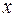 позволяет наедятся найти экстремальную задачу относительно переменных
позволяет наедятся найти экстремальную задачу относительно переменных 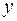 для которой также справедливы условия (6.4.8). Введем функцию
для которой также справедливы условия (6.4.8). Введем функцию
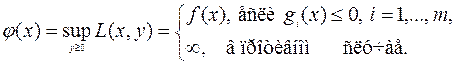 (6.4.9)
(6.4.9)
Поэтому исходная задача (6.4.1) может быть записана
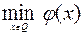 . (6.4.10)
. (6.4.10)
Образуем задачу, поменяв роль переменных и операций максимума и минимума. Введем
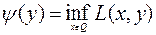 (6.4.11)
(6.4.11)
(возможно, что 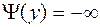 при некоторых
при некоторых 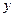 ) и рассмотрим задачу
) и рассмотрим задачу
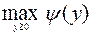 . (6.4.12)
. (6.4.12)
Задача (6.4.12) называется двойственной, а (6.4.1) или (6.4.10) – прямой.
Теорема 19 (теорема двойственности). Справедливы соотношения двойственности:
а) Для любых допустимых 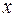 и
и 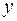 (т.е. для
(т.е. для 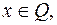
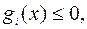
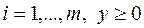 )
)
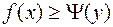 . (6.4.13)
. (6.4.13)
б) Если прямая задача регулярна, 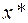 – ее решение,
– ее решение, 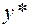 – множители Лагранжа, то
– множители Лагранжа, то 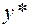 – решение (6.4.12) и
– решение (6.4.12) и
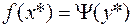 . (6.4.14)
. (6.4.14)
в) Если для допустимых, 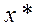 ,
, 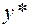 имеет место (6.4.14), то
имеет место (6.4.14), то 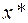 – решение прямой, а
– решение прямой, а 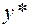 – решение двойственной задачи.
– решение двойственной задачи.
Максимум y(y) может достигаться лишь в точках, где 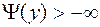 . Поэтому (6.4.12) равносильна задаче
. Поэтому (6.4.12) равносильна задаче
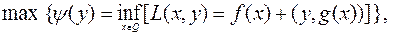 (6.4.15)
(6.4.15)
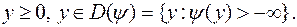
Значение теоремы двойственности в том, что при переходе к двойственной задаче при 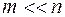 новая задача может оказаться существенно более простой, чем исходная. Этому способствуют возможность простого вычисления
новая задача может оказаться существенно более простой, чем исходная. Этому способствуют возможность простого вычисления 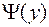 и ее производных и правильное распределение ограничений между множеством
и ее производных и правильное распределение ограничений между множеством 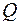 либо и множеством ограничений
либо и множеством ограничений 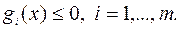
Единственность решения (6.4.1) гарантируется строгой выпуклостью функции 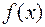 .
.
