Понятие предела функции, свойства
Министерство образования и науки Украины
Донецкий государственный университет
Экономики и торговли
Им. М. Туган-Барановского
Кафедра высшей и прикладной математики
 |
Методические рекомендации
Для практических занятий и самостоятельной работы
Студентов заочного отделения ФЭУМО
Донецк 2004
ББК 22.1я73
Ф 76
УДК 51:378 (076.5)
Рецензенты:
канд. физ.-мат. наук, доцент Е.К. Узбек
доцент В.М. Дрибан
Фомина Т.А.
Ф76 Высшая математика: Метод. реком. для студентов з/о ФЭУМО/ Фомина Т.А., Е.А. Данилейко – Донецк: ДонГУЭТ, 2004. – 59 с.
Методическая разработка предназначена для использования в учебном процессе и для самостоятельной работы студентов заочного отделения факультета ФЭУМО.
Цель разработки – помочь студентам освоить курс высшей математики в соответствии с учебной программой. Данная разработка может быть использована студентами других специальностей, а также студентами дневного отделения. Методические указания содержат следующие вопросы: дифференциальное исчисление функций одной переменной, интегральное исчисление, дифференциальные уравнения, ряды. Изложение теоретического материала сопровождает рассмотрению примеров с подробным их решением. Даются рекомендации по решению задач, которые предназначены в помощь студентам при выполнении контрольной работы.
ББК 22.1я73
| Ó Т.А. Фомина, Е.А. Данилейко, 2004 |
| Ó Донецкий государственный университет экономики и торговли им. М. Туган-Барановского, 2004 |
содержание
| Стр. | ||
| Введение…………………..………………………………………… | ||
| 1. | Введение в анализ……………………….…………………………… 1.1. Понятие предела функции, свойства…………………………….. 1.2. Раскрытие некоторых видов неопределенностей…………….... | |
| 2. | Дифференциальное исчисление функций одной переменной ….. 2.1. Понятие производной, свойства……………………………….… 2.2. Производные высших порядков………………………....………. 2.3. Дифференцирование некоторых функций……………………….. 2.4. Применение дифференциального исчисления к исследованию свойств функции одной переменной …………………………….. | |
| 3. | Интегральное исчисление…………………………………………… 3.1. Понятие неопределенного интеграла, свойства………….……. 3.2. Определенный интеграл. Основные свойства…………………… 3.3. Основные методы интегрирования……………………………… | |
| 4. | Дифференциальные уравнения……………………………………... 4.1. Основные понятия………………..………………………………. 4.2. Дифференциальные уравнения первого порядка………………... 4.3. Дифференциальные уравнения второго порядка с постоянными коэффициентами (однородные)…………………….…...……….. | |
| 5. | Ряды……………………..……………………………………………... 5.1. Основные понятия…………..……………………………………. 5.2. Достаточные признаки сходимости………………………….… 5.3. Степенные ряды…………………………………………………… | |
| 6. | Контрольная работа…...……………………………………………... | |
| Литература………………………………..…………………………… |
введение
В практической деятельности человека математика используется с момента своего зарождения. Долгое время развитие математики определялось в основном потребностями естественных и технических наук. И лишь последнее время математическое моделирование процессов и явлений постепенно проникло во все новые сферы научных знаний: физику, химию, биологию и, наконец, общественные науки, в частности, экономику, социологию, политологию.
Построение рыночных отношений в экономике требует повышения качества подготовки специалистов – выпускников высших учебных заведений.
Учитывая специфику учебного процесса студентов заочного отделения, возникает необходимость в методической разработке по основным темам курса высшей математики, которая предназначена для теоретического и практического изучения.
Знания, полученные при изучении курса математики, являются базовыми, на которые опираются такие математические курсы как теория вероятностей, математические методы исследования операций, а также ряда экономико-математических дисциплин.
В настоящей методической разработке рассматриваются следующие вопросы:
§ пределы;
§ дифференциальное и интегральное исчисление;
§ дифференциальные уравнения,
§ ряды.
Основная цель этого пособия – оказать помощь студентам факультета экономики, управления и международных отношений заочной формы обучения в выполнении контрольной работы.
Выбор варианта осуществляется следующим образом: берем две последние цифры номера зачетной книжки. Если число меньше или равно35,то это Ваш вариант; если это число больше 35, то отнимаем от него число, кратное 35, и получаем Ваш вариант.
Например: Если две последние цифры номера зачетной книжки 98, то  , значит, Ваш вариант: № 28.
, значит, Ваш вариант: № 28.
Работа, выполненная не по своему варианту, не зачитывается.
Правила оформление контрольной работы:
1. Контрольную работу необходимо выполнять в отдельной тетради, оставляя справа поля для замечаний рецензента.
2. В заголовке работы должны быть указаны фамилия и инициалы студента, факультет, курс, группа, учебный номер (шифр). Заголовок работы надо поместить на обложке тетради.
3. Необходимо записывать полное условие каждой задачи перед ее решением.
4. Решение задач записывать подробно, сопровождая необходимыми пояснениями.
5. В конце выполненной контрольной работы необходимо перечислить использованную при решении литературу.
6. Защита контрольной работы проводится в форме собеседования по теме работы.
І. Введение в анализ
Пусть каждому  поставлено в соответствие некоторое действительное число
поставлено в соответствие некоторое действительное число  , то есть рассматривается функция натурального аргумента. В этом случае говорят, что задана последовательность вещественных чисел, которую записывают в строчку в порядке возрастания номеров:
, то есть рассматривается функция натурального аргумента. В этом случае говорят, что задана последовательность вещественных чисел, которую записывают в строчку в порядке возрастания номеров:

или кратко: 
| Определение: | Число  называется пределом последовательности называется пределом последовательности  , если для любого (даже сколь угодно малого) , если для любого (даже сколь угодно малого)  существует номер существует номер  такой, что при всех такой, что при всех  выполняется неравенство: выполняется неравенство:  . . |
Геометрически определение предела означает, что начиная с некоторого номера, все члены последовательности окажутся в полосе  .
.









Если последовательность имеет предел, то говорят, что она сходится, в противном случае расходится.
Если  , то величина
, то величина  называется бесконечно малой. Величина, обратная бесконечно малой, является бесконечно большой:
называется бесконечно малой. Величина, обратная бесконечно малой, является бесконечно большой:
 .
.
Свойства.
1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
2. Произведение бесконечно малой на ограниченную величину будет бесконечно малым.
Понятие предела функции, свойства
Пусть функция 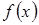 задана на интервале
задана на интервале  .
.
| Определение: | Число  называется пределом функции называется пределом функции 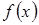 в точке в точке 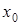 , если для любого , если для любого  существует существует  такое, что при всех такое, что при всех  , удовлетворяющих условию , удовлетворяющих условию   выполнено: выполнено:  . . |
| Определение: | Число  называется правосторонним (левосторонним) пределом функции называется правосторонним (левосторонним) пределом функции 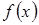 в точке в точке 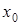 , если для любого числа , если для любого числа  существует существует  такое, что для любого такое, что для любого   выполнено: выполнено:  . . |
Обозначение:
§  (для левостороннего предела);
(для левостороннего предела);
§  (для правостороннего предела).
(для правостороннего предела).
Практическое вычисление пределов основано на следующих теоремах:
1. Функция 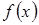 имеет в точке
имеет в точке 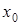 предел тогда и только тогда, когда в этой точке существуют правосторонний и левосторонний пределы и они равны. В этом случае предел функции равен односторонним пределам.
предел тогда и только тогда, когда в этой точке существуют правосторонний и левосторонний пределы и они равны. В этом случае предел функции равен односторонним пределам.
2. Арифметические действия над пределами:
Если  и
и  , то справедливы утверждения:
, то справедливы утверждения:
§  ;
;
§  ;
;
§  , при условии, что
, при условии, что  .
.
1. Первый замечательный предел:
 . (1.1)
. (1.1)
2. Второй замечательный предел:
 или
или  . (1.2)
. (1.2)
