Определение объёма испытаний

Величина возможной ошибки зависит от объёма испытаний, конструктивных особенностей испытуемых элементов, материала, условий испытания и методики обработки их результатов. Повысить точность оценки характеристик при определённых условиях испытаний можно только путём увеличения объема испытаний и применения более рациональной методики статической обработки результатов, использующей максимум информации, полученной при экспериментах.

При определении минимального объёма выборки n следует исходить из целей предстоящих испытаний.

Если испытания проводят с целью оценки математического ожидания а, то объём выборки в предположении нормального распределения определяют по формуле

n = 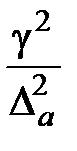z²_1-α/2 (2.31)

или

n = 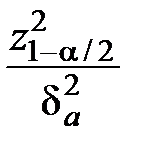(2.32)

где γ – коэффициент вариации определяемой характеристики; Δ_a – максимальная относительная ошибка (допуск) при оценке среднего значения в долях среднего значения определяемой характеристики; z²_1-α/2 – квантиль уровня Р = 1 – α/2 нормированной нормально распределённой случайно величины; Р₁ = 1 – α – статическая надёжность, представляющая собой вероятность непревышения фактической ошибкой при оценке среднего значения характеристики максимальных ошибок Δ_a или δ_a (по модулю); δ_a – максимальная относительная ошибка (допуск) при оценке среднего значения в долях среднего квадратического отклонения изучаемой характеристики.

Как правило, генеральный коэффициент вариации γ является неизвестной величиной, поэтому при определении объёма выборки его заменяют коэффициентом ν, полученным на основе априорной информации. При отсутствии аналога значением выборочного коэффициента вариации задаются и уточняют в процессе эксперимента. В этом случае объём испытаний должен быть скорректирован в соответствии с уточнённым значением коэффициента вариации методом подбора по формуле

n = 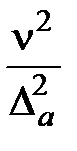t²_α,k (2.33)

где t_α,k – значение квантили статистики t уровня Р = 1 – α/2 для числа степеней свободы k = n – 1 (см. таблица 2.8).

Формулы (2.31)–(2.33) получены из условия, что вероятность попадания оценки математического ожидания в интервал а(1 ± Δ_а) или а ± δ_а σ будет Р = 1 – α.

Величину максимальных ошибок Δ_a или δ_a следует выбирать в зависимости от требований к точности оценки среднего значения исследуемой характеристики. При низкой точности величину Δ_a принимают равной коэффициенту вариации определяемой характеристики, в этом случае δ_а = 1. При средней точности Δ_a принимают равной (0,4 …0,5)γ и δ_а = 0,4 … 0,5, при высокой точности – Δ_a = (0,2 …0,3)γ и δ_а = 0,2 … 0,3.

Пример 2.8. Определить необходимый объём испытаний образцов с целью оценки среднего значения, если α = 0,1 и Δ_a = 0,02. Данные о коэффициенте вариации при аналогичных испытаниях отсутствуют.

Задаёмся коэффициентом вариации γ = 0,04. По таблице 2.7 для α = 0,1 находим z_0,95 = 1,645 и по формуле (2.31) определяем

n = 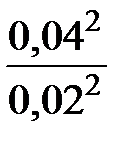1,645² ≈ 11.

Пусть по испытаниям 11 образцов выборочный коэффициент вариации составил ν = 0,051. В этом случае производим корректировку необходимого объёма испытаний, для чего формулу (2.33) представляем в виде

Δ_a = 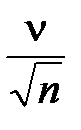t_α,k (2.34)

Так как выборочный коэффициент вариации оказался больше первоначально принятого γ, то при n = 11 фактическая ошибка будет больше Δ_a = 0,02.

Задаёмся n = 15 и определяем по формуле (2.34) ожидаемую ошибку, по таблице 9 – t_0,1,14 = 1,761,

Δ_a = 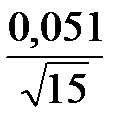1,761 = 0,0232,

что больше заданной ошибки Δ_a = 0,02.

В качестве следующего приближения задаёмся n = 20. t_0,1,19 = 1,73.

Δ_a = 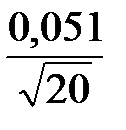1,73 ≈ 0,02.

Итак, принимаем n = 20, т. е. дополнительно испытываем 9 образцов.

Пусть далее по результатам испытаний n = 11 + 9 = 20 образцов выборочный коэффициент вариации ν = 0,045. Определяем по формуле (2.34) ожидаемую с вероятностью Р = 0,9 максимальную относительную ошибку оценки среднего значения предела прочности

Δ_a = 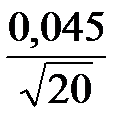1,761 = 0,0177.

Если после дополнительных девяти образцов выборочный коэффициент вариации оказался бы существенно выше 0,051, а величина максимальной ошибки, подсчитанная по формуле (2.34), была бы неприемлимо высокой, то следовало бы вновь скорректировать объём испытаний с учётом полученного значения после дополнительных испытаний коэффициента вариации и т.д.

Если цель планируемых испытаний – оценка среднего квадратического отклонения характеристики, то объём выборки определяют методом подбора по формуле

(1 + Δ_σ)² = 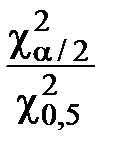, (2.35)

где Δ_σ – максимальная относительная ошибка (допуск) при оценке среднего квадратического отклонения случайной величины при нормальном законе распределения; χ²_α/2 и χ²_0,5 – квантили уровня Р = α/2 и Р = 0,5 статистики χ² (таблица 2.9).

Значение ошибки Δ_σ следует выбирать в зависимости от требований к точности оценки среднего квадратического отклонения характеристики. При низкой точности принимают Δ_σ = 0,4 … 0,5, при средней точности Δ_σ = 0,25 … 0,35 и при высокой точности Δ_σ = 0,1 … 0,2.

При n ≥ 15 для определения объёма выборки вместо (2.35) можно воспоьзоваться приближённой формулой

n = 1,5 + 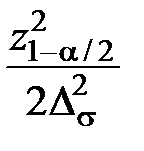, (2.36)

Пример 2.9. Определить минимально необходимый объём испытаний с целью оценки среднего квадратического отклонения, если α = 0,1 и Δ_σ = 0,3.

Подсчитываем левую часть уравнения (2.36)

(1 + Δ_σ)² = (1 + 0,3)² = 1,69

По таблице 2.10 для различных k = n – 1 вычисляем отношения χ²_0,05 и χ²_0,5, выбираем такое значение k = n – 1, при котором отношение указанных величин будет меньше или равняться значения левой части уравнения (2.35).

Для k = 10

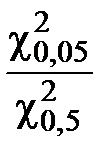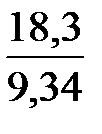= = 1,96

Для k = 15

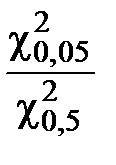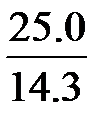= = 1,75

Для k = 16

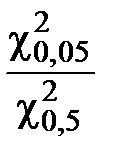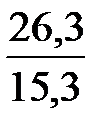= = 1,72

Для k = 17

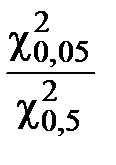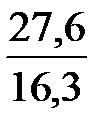= = 1,69

Окончательно принимаем n = k + 1 = 18

При использовании формулы (2.36) получаем

n = 1,5 + 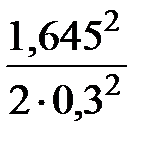= 16,5 ≈ 17.

Если в результате испытаний планируется одновременная оценка и среднего значения, и среднего квадратического отклонения контролируемой характеристики с заданной точностью и надёжностью, то объём испытаний определяют как наибольшее из двух значений n, найденных по формулам (2.31) – (2.33) и (2.35) – (2.36).

Для этой цели могут быть также использованы таблицы 2.10 и 2.11.

Таблица 2.10 – Минимальное число образцов n для оценки среднего значения, рассчитанное по формуле (2.31)

γ	Δα
0,01	0,02	0,03	0,04	0,05
α
0,05	0,10	0,05	0,10	0,05	0,10	0,05	0,10	0,05	0,10
0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10

Таблица 2.11 – Минимальное число образцов n для оценки среднего квадратического отклонения, рассчитанное по формуле (2.35)

α	Δσ
0,1	0,2	0,3	0,4	0,5
0,05 0,06 0,07 0,08 0,09 0,10

Приложение А