Типовой расчёт. «Теория поля»
Задача 1. Дано векторное поле 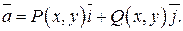
1. Проверить, что это поле является потенциальным.
2. Найти потенциал поля 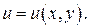
3. Найти уравнение линий равного потенциала и изобразить линии равного потенциала на чертеже.
4. Составить уравнение векторных линий поля 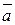 и изобразить векторные линии на том же чертеже, указав стрелками направление векторных линий.
и изобразить векторные линии на том же чертеже, указав стрелками направление векторных линий.
5. Вычислить линейный интеграл 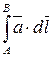 .
.
| Вар. | Векторное поле | Точка A | Точка B |
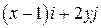 | 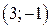 |  | |
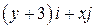 | 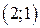 | 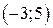 | |
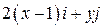 | 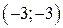 | 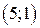 | |
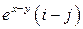 | 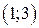 | 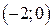 | |
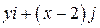 |  | 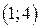 | |
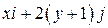 | 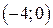 | 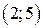 | |
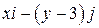 | 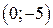 | 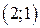 | |
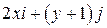 | 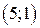 | 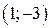 | |
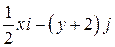 | 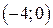 | 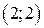 | |
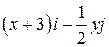 | 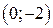 | 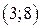 | |
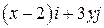 | 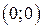 | 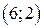 | |
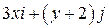 | 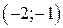 | 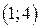 | |
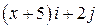 | 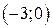 | 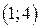 | |
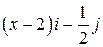 | 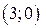 | 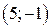 | |
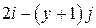 | 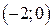 | 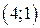 | |
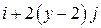 | 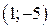 | 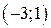 | |
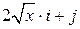 | 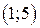 | 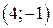 | |
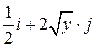 | 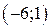 | 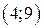 | |
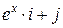 | 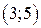 | 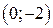 | |
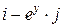 | 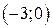 | 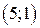 | |
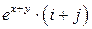 | 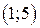 | 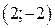 | |
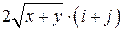 | 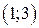 | 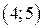 | |
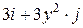 | 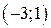 | 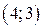 | |
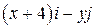 | 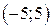 | 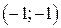 | |
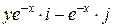 | 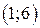 | 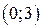 | |
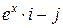 | 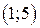 | 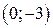 | |
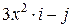 |  | 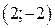 | |
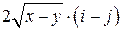 | 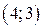 | 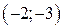 | |
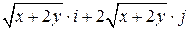 | 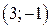 | 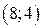 | |
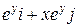 | 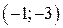 | 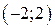 |
Задача 2. Дано векторное поле 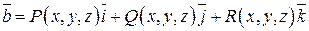 .
.
1. Найти дивергенцию векторного поля 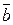 , исследовать расположение источников и стоков векторных линий поля.
, исследовать расположение источников и стоков векторных линий поля.
2. Найти поток векторного поля 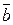 через замкнутую поверхность
через замкнутую поверхность 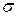 .
.
3. Найти ротор векторного поля 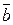 .
.
4. Вычислить циркуляцию поля 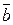 вдоль замкнутой линии
вдоль замкнутой линии  двумя способами: а) преобразовав линейный интеграл в определенный с использованием уравнений линии
двумя способами: а) преобразовав линейный интеграл в определенный с использованием уравнений линии  ; б) преобразовав линейный интеграл в поверхностный с помощью теоремы Стокса.
; б) преобразовав линейный интеграл в поверхностный с помощью теоремы Стокса.
5. Выяснить, как изменится циркуляция поля 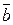 вдоль контура
вдоль контура  , если изменить расположение контура в данном поле. Найти наибольшее значение циркуляции для данного контура.
, если изменить расположение контура в данном поле. Найти наибольшее значение циркуляции для данного контура.
| Вар. | Поле 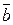 : : 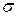 - поверхность, ограничивающая тело Т. - поверхность, ограничивающая тело Т.  - замкнутая линия - замкнутая линия |
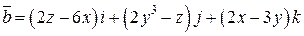  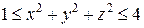 . .  -контур прямоугольника с вершинами -контур прямоугольника с вершинами 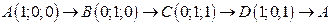 | |
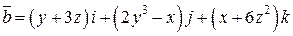  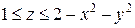 . .  состоит из дуги окружности состоит из дуги окружности 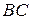 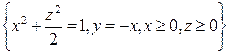 и двух отрезков прямых и двух отрезков прямых 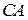 и и 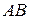 , , 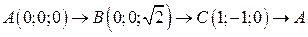 | |
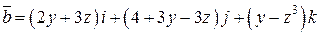  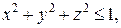 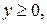 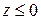 . .  -контур треугольника с вершинами -контур треугольника с вершинами 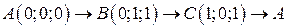 | |
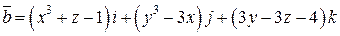  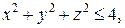 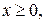 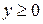 . .  -контур треугольника с вершинами -контур треугольника с вершинами 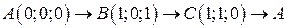 | |
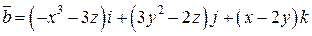  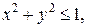 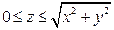 . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами 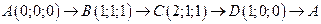 | |
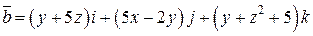  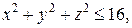 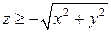 . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами 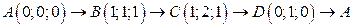 | |
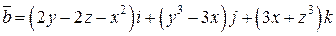  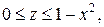 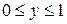 . .  -контур треугольника с вершинами -контур треугольника с вершинами 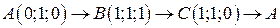 | |
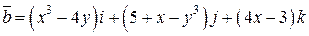  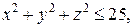 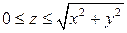 . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами 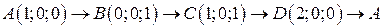 | |
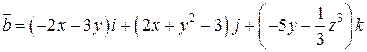  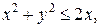 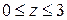 . .  -контур треугольника с вершинами -контур треугольника с вершинами 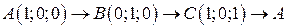 | |
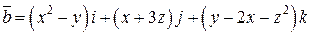  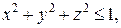 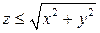 . .  -контур треугольника с вершинами -контур треугольника с вершинами 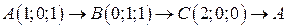 | |
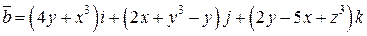  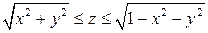 . .  -контур треугольника с вершинами -контур треугольника с вершинами 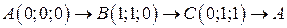 | |
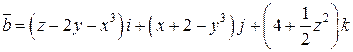  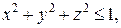 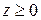 . .  -контур треугольника с вершинами -контур треугольника с вершинами 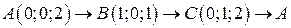 | |
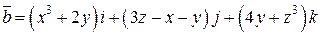  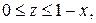 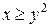 . .  состоит из дуги эллипса состоит из дуги эллипса 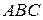 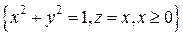 и его диаметра и его диаметра 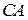 : : 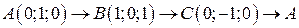 | |
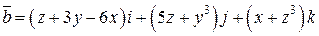  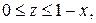 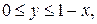 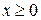 . .  -эллипс -эллипс 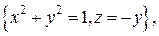 обходимый в направлении обходимый в направлении 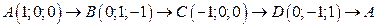 | |
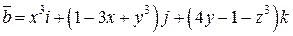  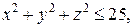 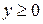 . .  -контур треугольника с вершинами -контур треугольника с вершинами 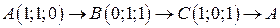 | |
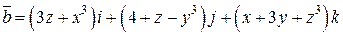  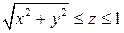 . .  -контур прямоугольника с вершинами -контур прямоугольника с вершинами 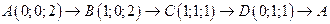 | |
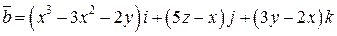  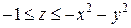 . .  -контур треугольника с вершинами -контур треугольника с вершинами 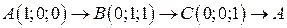 | |
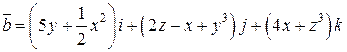  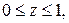 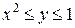 . .  состоит из дуги окружности состоит из дуги окружности 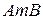 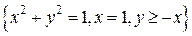 и ее диаметра и ее диаметра 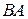 : : 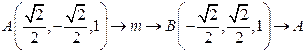 | |
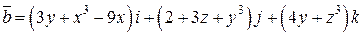  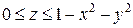 . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами 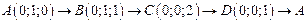 | |
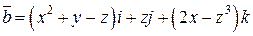  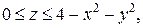 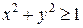 . .  -контур треугольника с вершинами -контур треугольника с вершинами 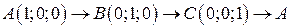 | |
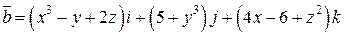  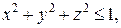 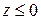 . .  -контур ромба с вершинами -контур ромба с вершинами 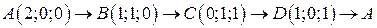 | |
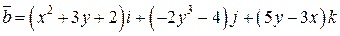  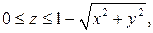 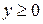 . .  -контур прямоугольника с вершинами -контур прямоугольника с вершинами 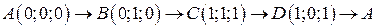 | |
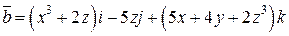  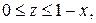 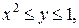 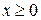 . .  состоит из дуги эллипса состоит из дуги эллипса 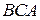 : : 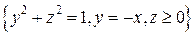 и его диаметра и его диаметра 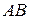 , , 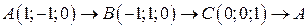 | |
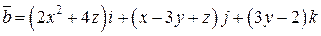  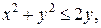 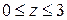 . .  -контур треугольника с вершинами -контур треугольника с вершинами 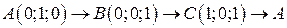 | |
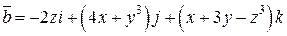  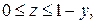 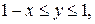 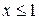 . .  состоит из дуги окружности состоит из дуги окружности 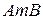 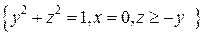 и ее диаметра и ее диаметра 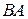 : : 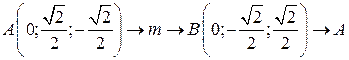 | |
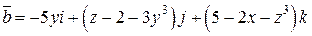  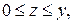 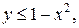 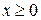 . .  - контур ромба с вершинами - контур ромба с вершинами 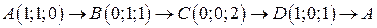 | |
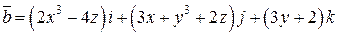  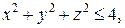 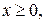 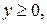 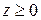 . .  -контур треугольника с вершинами -контур треугольника с вершинами 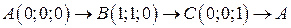 | |
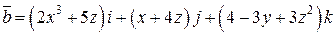  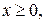 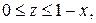 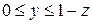  - состоит из дуги окружности - состоит из дуги окружности 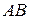 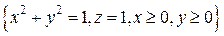 и двух отрезков прямых и двух отрезков прямых 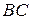 и и 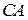 : : 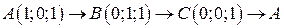 | |
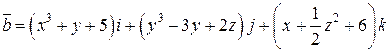  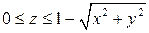 . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами 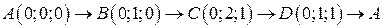 | |
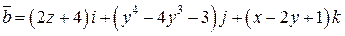  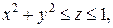 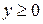 . .  -контур прямоугольника с вершинами -контур прямоугольника с вершинами 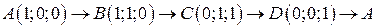 |
Список литературы.
1.Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.2, изд.13. – М.:Наука,1985.560 с.
2.Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного.- М.:Наука,1989.464 с.
3. Кудрявцев Л.Д.Курс математического анализа Т.1,2. -М.: Высшая школа,1981.614с.;470 с.
4. Гаврилов В.Р., Иванова Е.Е., Морозова В.Д. Кратные и криволинейные интегралы. Элементы теории поля. Учебник для вузов. Под ред. В.С. Зарубина, А.П. Крищенко. Серия «Математика в техническом университете». Вып. VII.- М.:МГТУ,2001.492 с.
5. Осипова М.З. Теория поля. Учебное пособие по выполнению контрольного задания. - М.:МВТУ,1978.
Оглавление.
1. Скалярные и векторные поля. 4
2. Поверхности и линии уровня. 5
3. Производная по направлению скалярного поля. 7
4. Градиент скалярного поля. 9
5. Векторные линии векторного поля. 12
6. Криволинейный интеграл векторного поля. 15
7. Потенциальное векторное поле. 20
8. Поток векторного поля. 28
9. Дивергенция векторного поля. Соленоидальное векторное поле. 32
10. Ротор (вихрь) векторного поля. Формула Стокса. 37
11. Операторы Гамильтона и Лапласа. 44
12. Ответы к контрольным заданиям. 47
13. Типовой расчёт «Теория поля». 49
