Вопрос 11.3. Главное значение несобственного интеграла

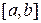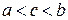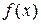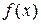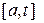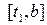Пусть на отрезке , за исключением точки c ( ), определена функция . Пусть функция имеет в точке c особенность и интегрируема на отрезках и , где 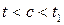. Тогда, если существуют предел

,

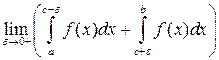то его называют главным значением несобственного интеграла и обозначают

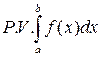
или

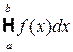
Пример 11.8. Вычислить интеграл

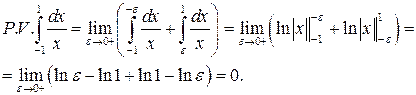
В тоже время этот интеграл как несобственный является расходящимся.

Конец примера.

ЛЕКЦИЯ № 12. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.

Вопрос 12.1. Функции нескольких переменных. Основные понятия и определения.

Определение 12.1. N-мерным арифметическим пространством называется множество упорядоченных наборов из n вещественных чисел 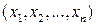. Число n называется размерностью пространства, а сами наборы называются точками. Числа 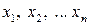называются координатами точек. Две точки пространства называются равными, если они имеют одинаковые координаты.

Пример 12.1. Пусть на плоскости введена декартова система координат, тогда каждой точке плоскости можно поставить в соответствие пару чисел, ее координаты. Следовательно, плоскость есть двухмерное арифметическое пространство. Аналогично устанавливается, что числовая прямая есть одномерное арифметическое пространство, а обычное пространство - есть трехмерное арифметическое пространство. Если в вести в рассмотрение время - четвертую координату, то получаем четырехмерное арифметическое пространство.

Конец примера.

Замечание 12.1. В современной математике под пространством понимают множество объектов произвольной природы, наделенное некоторой структурой.

Определение 12.2. Пусть на некотором множестве M из арифметического пространства T размерности n каждой точке этого множества по некоторому правилу или закону поставлено в соответствие одно и только одно вещественное число. Тогда говорят, что на множестве M задана вещественная функция n переменных. Множество M называют областью определения или областью задания функции f. Множество чисел, которое поставлено в соответствие к множеству M называется множеством значений функции. Точки из множества M называют аргументом функции. Координаты точек так же называют аргументами функции.

Будем обозначать функции нескольких переменных следующими символоми

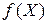‑ если не нужен список аргументов,

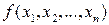‑ указан список аргументов,

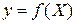‑ если нужно указать значение функции.

Функции двух и трех переменных обычно обозначают так: 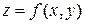и .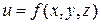

Определение 12.3. Графиком функции n переменных 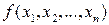называют множество точек n+1 мерного арифметического пространства вида .

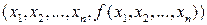Для функции двух переменных график есть поверхность в трехмерном пространстве (смотри рис. 1), поэтому по аналогии в общем случае график функции называют n мерной поверхностью.

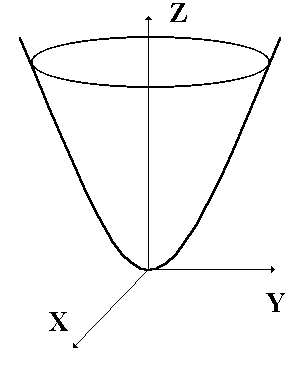
Рис. 1. График функции .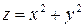

Определение 12.4. Поверхностью равного уровня функции нескольких переменных называют n мерную поверхность, на которой функция принимает постоянное значение. Для функции двух переменных вместо поверхности равного уровня используется термин линия равного уровня.

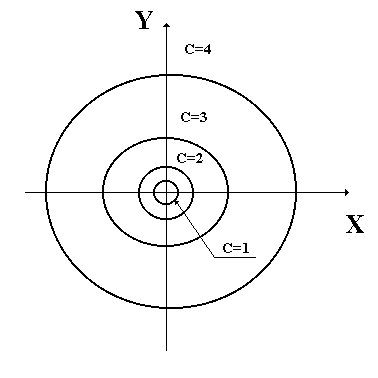
Рис 2. Линии постоянного уровня для функции .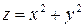

Поверхности и линии равного уровня используются для наглядного представления функции и анализа ее поведения.