Простые зубчатые механизмы

7.1 Структурный анализ простого зубчатого механизма

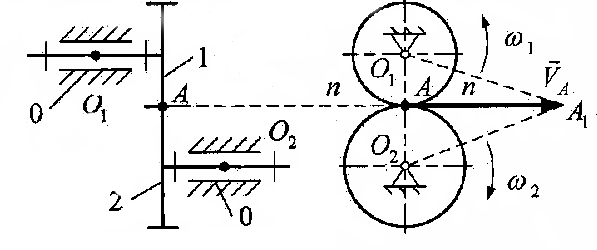
Структурный анализ простых зубчатых механизмов сводится к определению подвижности механизма.

Подвижность механизма определяемпо формуле Чебышева:

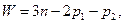
где W- подвижность механизма;

n - число подвижных звеньев;

p₁ и p₂ - соответственно число пар пятого и четвертого класса.

№	схема	Название/ кинематическое состояние
		Зубчатое колесо/ подвижное

		Зубчатое колесо/ подвижное
		Стойка/ неподвижное

В структуру механизма входят два подвижных звена (зубчатые колеса) и стойка, представленная двумя шарнирно-неподвижными опорами. Следовательно, n=2.

№/название	схема	Класс/ подвижность	Вид контакта/ замыкание
0-1/ Вращатель-ная		5/1	Поверхность/ геометрическое

0-2/ Вращатель-ная		5/1	Поверхность/ геометрическое
1-2/ зубчатая		4/2	Линия/ геометрическое

Кинематические пары 0-1 и 0-2 являются вращательными парами пятого класса, следовательно, p₁=2.

В структуру механизма входят два подвижных звена (зубчатые колеса) и стойка, представленная двумя шарнирно-неподвижными опорами. Следовательно, n=2.

Кинематические пары 0-1 и 0-2 являются вращательными парами пятого класса, следовательно, p₁=2.

Кинематическая пара 1-2 является парой четвертого класса, следовательно, p₂=1.

Подставим число подвижных звеньев и число пар пятого и четвертого классов в формулу Чебышева:

.

Полученный результат означает, что для однозначного описания положения всех звеньев механизма в рассматриваемой плоскости достаточно знать одну обобщенную координату.

7.2 Синтез эвольвентного зацепления простого зубчатого механизма

Найдем инвалюту угла зацепления:

,

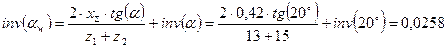По таблице значений инвалют найдем угол зацепления:

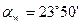
Найдем минимальную величину коэффициента смещения для шестерни:

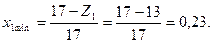
Найдем коэффициент смещения для колеса:

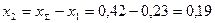
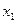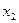Отложим значение смещения и на осях блокирующего контура. Точка их пересечения должна находится в блокирующем контуре. В данном случае точка находится в контуре, точка 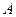, следовательно оставляем полученные значения коэффициентов для дальнейших расчетов.

Найдем геометрические параметры зубчатых колес.

Диаметры делительных окружностей:

для шестерни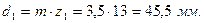

для колеса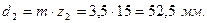

где 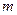- модуль;

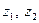- число зубьев на шестерне и колесе соответственно.

Диаметры начальных окружностей:

для шестерни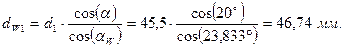

для колеса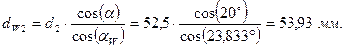

Шаг по делительной окружности:

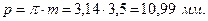
Шаг по основной окружности:

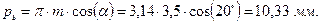
Диаметры основных окружностей:

для шестерни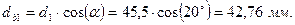

для колеса

Диаметры окружностей впадин зубьев:

для шестерни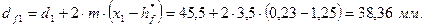

для колеса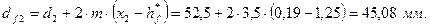

где 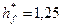- - коэффициент ножки зуба.

Диаметры окружностей вершин зубьев:

для шестерни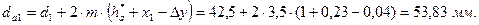

для колеса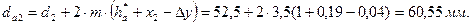

где 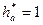- коэффициент головки зуба.

Коэффициент уравнительного смешения:

.

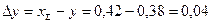Коэффициент воспринимаемого смешения:

.

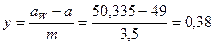Уточненное межосевое расстояние:

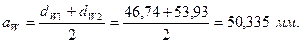
Делительное межосевое расстояние:

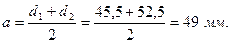
Толщина зуба по делительной окружности:

для шестерни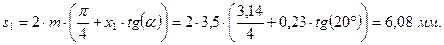

для колеса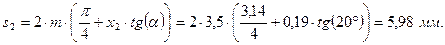

Толщина впадин по делительной окружности:

для шестерни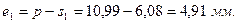

для колеса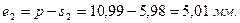

Высота зубьев:

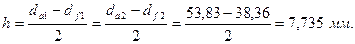
Углы профиля на окружности вершин:

для шестерни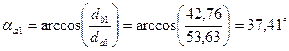

для колеса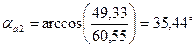

Толщина зубьев по окружности вершин:

для шестерни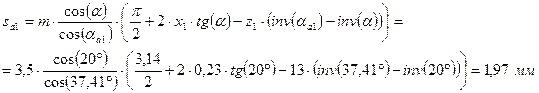

для колеса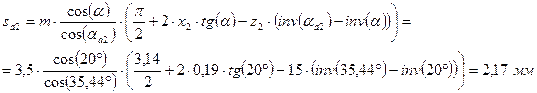

Проверка:

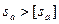, где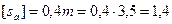

Оба значения толщины зубьев по окружности больше значения минимальной толщины, проверка сходится.

Коэффициент торцевого перекрытия:

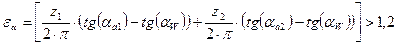(7.1)

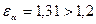
Для построения зубчатого зацепления определим масштабный коэффициент длин и переведем все геометрические параметры зубчатых колес в данный масштабный коэффициент, при условии, что высота зуба должна быть не менее 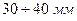на чертеже.

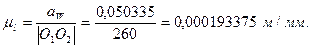
Переведем все значения через :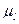

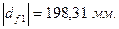
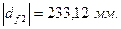
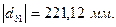
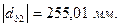
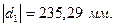
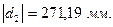
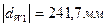
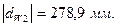
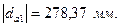
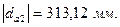
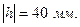
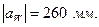
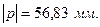
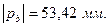
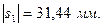
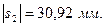
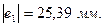
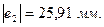
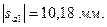
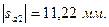
Для построения зубчатого зацепления отложим межосевое расстояние ( 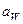). Проведем начальную, делительную, основную окружности, а также окружности вершин и впадин зубьев для каждого зубчатого колеса. Начальные окружност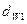и ( и 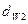) должны сопрягаться в полюсе зацепления ( 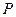). Откладываем под углом ( 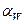) от линии центров ( 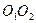) для колеса и для шестерни лучи, пересекающие основные окружности в точках 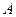и 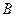. Через точк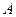и и 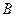проводим прямую - линию зацепления. Она проходит через полюс зацепления ( 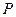). Отрезок от точки сопряжения ( 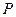) до точки пересечения ( 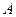), делим на шесть равных частей а_i. Проецируем полученные точки на основную окружность, проводим через каждую из них касательную к основной окружности, и на касательных откладываем величину отрезка ( 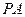), каждый раз уменьшая на величину а_i. Полученные точки соединяем плавной кривой и получаем нижнюю половину эвольвентного профиля зуба. Аналогично построим вторую половину профиля зуба, только увеличивая отрезок 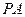на величину а_i. Откладываем толщину зуба по делительной окружности и ширину зуба по окружности вершин. Симметрично отобразим вторую половину профиля зуба. По делительной окружности откладывая ширину впадины и шаг, строим еще два - три зуба. Аналогично строим профили зубьев шестерни.

Сложный зубчатый механизм

8.1 Структурный анализ

Данный сложный зубчатый механизм образован соединением трёх простых зубчатых передач и планетарного механизма.

Сложный зубчатый механизм является плоским, следовательно, подвижность определяем по формуле Чебышева:

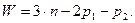(8.1)

Составим таблицу по которой определим количество подвижных звеньев:

№ п.п	Номер звена	Вид совершаемого движения	Схема	Кинематическое состояние
		вращательное		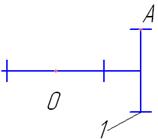подвижное
	2	вращательное		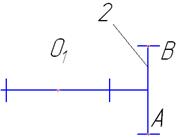подвижное
	3 – 3’	вращательное		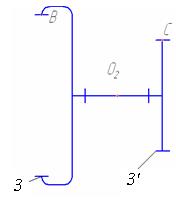подвижное
	4–4’	сложное		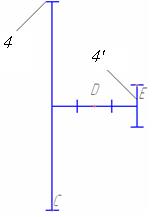подвижное
	Н-6	вращательное		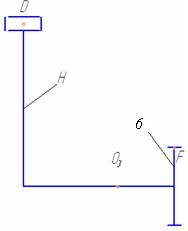подвижное
	5	-		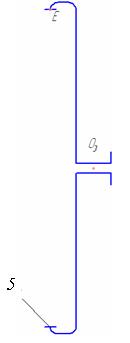Неподвижное
		вращательное		подвижное

Анализируя схему, видим, что механизм состоит из стойки 0, представленной четырьмя шарнирно неподвижными опорами, и шестью подвижными звеньями (1; 2; 3-3'; 4-4`; Н-6; 7).

Колесо 5 является неподвижным звеном и относится к стойке. Таким образом, n=6.

Для определения класса кинематических пар составив следующую таблицу:

Номер звена	Схема	Название	Класс/ подвижность	Вид контакта/замыкание
0 – 1		вращательная	5/1	По поверхности(низшая)/ геометрическое
1 – 2		зубчатая	4/2	Линия (высшая)/ геометрическое
0 – 2		вращательная	5/1	По поверхности(низшая)/ геометрическое
2 – 3,3’		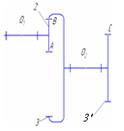зубчатая	4/2	Линия (высшая)/ геометрическое
3,3’ – 0		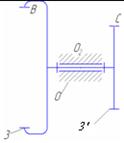вращательная	5/1	По поверхности(низшая)/ геометрическое
3,3’ – 4,4’		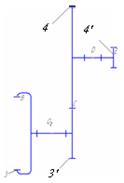зубчатая	4/2	Линия (высшая)/ геометрическое
4,4’ – Н		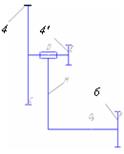вращательная	5/1	По поверхности(низшая)/ геометрическое
4,4’ – 5		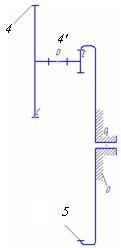зубчатая	4/2	Линия (высшая)/ геометрическое
5 – Н,6		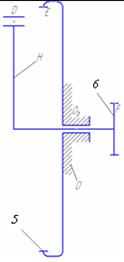вращательная	5/1	По поверхности(низшая)/ геометрическое
Н,6 – 7		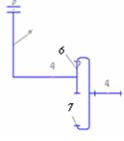зубчатая	4/2	Линия (высшая)/ геометрическое
7 – 0		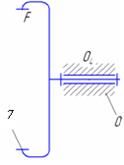вращательная	5/1	По поверхности(низшая)/ геометрическое

Схема содержит шесть одноподвижных кинематических пар: 0-1; 0-2; H-4,4`; 0-3,3’, Н-5; 0-7. И пять высших двухподвижных кинематических пар: 1-2; 2-3,3’; 3,3’-4,4’; 4,4`-5; H,6-7;

Следовательно, р₁=6; р₂=5.

Подставив найденные значения в формулу (8.1), получим:

.

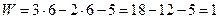Полученный результат означает, что для однозначного описания положения всех звеньев механизма в рассматриваемой плоскости достаточно знать одну обобщенную координату.

8.2 Синтез сложного зубчатого механизма

Поскольку данный сложный зубчатый механизм состоит из четырёх ступеней (рядов) – планетарной и трёх простых, то передаточное отношение 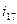следует разбить на произведение четырех отношений:

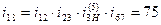. (8.2)

Проверим возможность реализации заданного передаточного отношения:

.

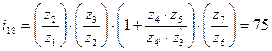Разложим передаточное число по ступеням (рядам):

.

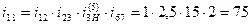Передаточное отношение первого ряда:

,

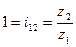тогда .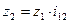

Из условия отсутствия интерференции:

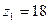, следовательно, .

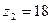Передаточное отношение второго ряда:

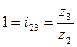(8.3)

тогда .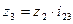

Из условия отсутствия интерференции:

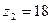, следовательно, .

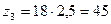Передаточное отношение третьего ряда:

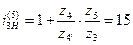. (8.4)

Выразим из (8.3) :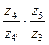

.

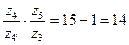Представим передаточные числа в виде сомножителей:

.

Следовательно:

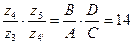
Рассмотрим три варианта числа зубьев для каждого колеса:

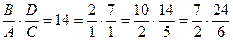
Запишем условие соосности: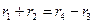

,

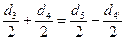где d_i – делительный диаметр колес: .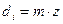

,

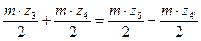Сократим на m/2 все слагаемые в обеих частях уравнения, получим:

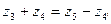. (8.4)

Выражение (8.4) отображает условие соосности двухрядного планетарного механизма с одним внешним и одним внутренним зацеплениями.

Выразим условие соосности через сомножители:

,

,

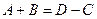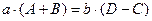где a=(D-C);

b=(A+B).

Выразим числа зубьев через коэффициенты:

.

Произведем расчет чисел зубьев для трех вариантов и занесем все значения в таблицу 7.

Таблица 7 – числа зубьев колес

Вар-т	A	B	C	D	a	b	Z3	Z4	Z4’	Z5	q
	1	2	1	7	6	3	6	12	3	21	1
	42	84	21	147	7
	2	10	5	14	9	12	18	90	60	168	1
	2	7	6	24	24	9	36	126	54	216	1

В данной схеме планетарного механизма необходимо обеспечить отсутствие подреза зубьев колес. Для выполнения этого условия необходимо, чтобы число зубьев всех колес было больше или равно семнадцати. Из таблицы 7 видим, что это условие не выполняется в первом варианте, следовательно общий сомножитель q в первом варианте будет равен 7.

Для обеспечения отсутствия контакта сателлитов друг с другом необходимо проверить условие соседства:

,

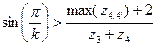где k – число сателлитов;

max(z_4,4’) – Максимальное число зубьев сателлитов. В данном случае, число зубьев колеса 4` больше, значит в формулу подставляем z_4’;

z₅ и z_4’ – число зубьев солнечного колеса и сателлита соответсвенно.

Рассмотрим условие соседства для всех вариантов:

Вариант 1:

; .

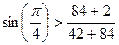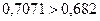Следовательно, условие соседства для первого варианта выполняется.

Вариант 2:

; .

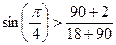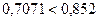Следовательно, условие соседства для второго варианта не выполняется.

Вариант 3:

; .

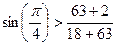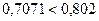Следовательно, условие соседства для третьего варианта не выполняется.

Условие соседства выполняется для первого варианта, следовательно, в качестве окончательного принимаем вариант1.

Передаточное отношение четвертого ряда:

,

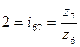тогда .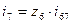

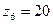, следовательно, .

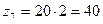Определим диаметры зубчатых колес механизма.

,

,

,

,

,

,

,

,

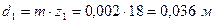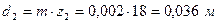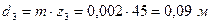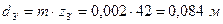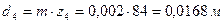
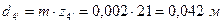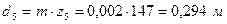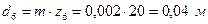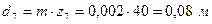Рассчитаем масштабный коэффициент длин для данной схемы:

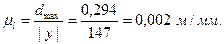
Переведем все диаметры в масштабный коэффициент:

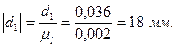
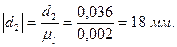
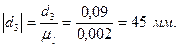
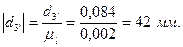
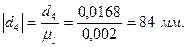
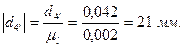
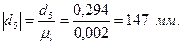
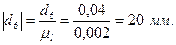
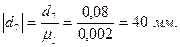
Построим кинематическую схему механизма в найденном масштабном коэффициенте. Расстояние между колесами берем произвольным, поскольку оно не влияет на передаточную функцию механизма.

8.3 Кинематический анализ

Построим план скоростей для данной схемы сложного зубчатого механизма. По условию имеем число оборотов на первом колесе .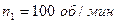

Определим угловую скорость на первом колесе:

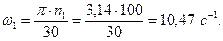
Найдем линейную скорость первого колеса:

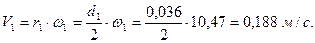
Найдем масштабный коэффициент скоростей:

,

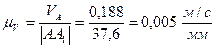где |AA₁| - отрезок, изображающий скорость точки А на плане скоростей.

Построим план угловых скоростей методом параллельного переноса годографов с плана скоростей на план угловых скоростей от полюса и до пересечения с осью ω. Расстояния от нуля до найденных точек и есть значения величин угловых скоростей.

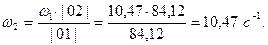
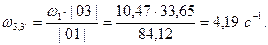
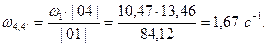
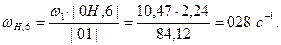
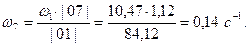
Определим передаточное число через полученные в ходе кинематического анализа значения угловых скоростей:

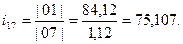
Подсчитаем погрешность:

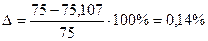
Погрешность не более 5%, следовательно расчет СЗМ верен.
9 Кулачковый механизм

Кулачковый механизм – это механизм с высшей кинематической парой, обладающий возможностью обеспечения выстоев выходного звена, а структура содержит хотя бы одно звено с рабочей поверхностью переменной кривизны.

9.1 Структурный анализ

Так как все звенья данного механизма лежат в одной плоскости, то его подвижность рассчитывается по формуле Чебышева:

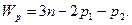
Для определения количества подвижных звеньев составляем таблицу:

№	схема	Название звена/ вид движения
		Кулачок/вращательное
		Толкатель/вращательное
		Ролик/сложное
		Стойка/неподвижное

Механизм состоит из стойки и трех подвижных звеньев: кулачка 1, толкателя 2 и ролика 3. Ролик введен в схему механизма для замены трения скольжения на трение качения, с целью уменьшения интенсивности износа рабочих поверхностей контактирующих звеньев, а также с целью увеличения КПД и ресурса работы механизма.

№	схема	Класс/ подвижность	Вид контакта/ замыкание
0-1		5/1	Поверхность/ геометрическое
0-2		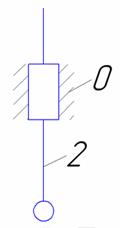5/1	Поверхность/ геометрическое
3-2		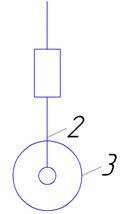5/1	Поверхность/ геометрическое
1-3		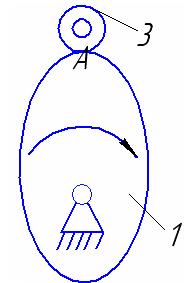4/2	Линия/силовое

Ролик образует с выходным звеном поступательную кинематическую пару пятого класса. Подвижность этой кинематической пары не изменяет подвижности кулачкового механизма, не влияет на его передаточную функцию, так как является местной подвижностью.

Звенья 1 и 2 образуют со стойкой низшие кинематические пары 0-1;

0-2; кинематическая пара 2-3 является дефектом структуры с местной подвижностью, равной 1, следовательно 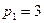Кинематическая пара 1-3 является высшей, следовательно .

.

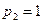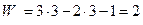При удалении дефекта структуры, получим:

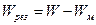
где 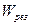- подвижность механизма в результате удаления дефектов;

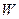- подвижность механизма;

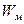- местная подвижность.

Следовательно, подвижность равна:

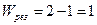
9.2 Функция аналога пути

Для построения диаграммы зависимости перемещения от угла поворота кулачка вычислим перемещение:

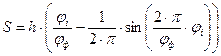
где 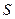- перемещение, м;

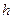- ход кулачкового механизма, м;

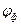- фазовый угол соответствующей фазы, рад;

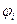- текущее значение фазового угла, рад.

Ход механизма с толкателем равен:

,

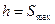Определим масштабный коэффициент оси аналога пути:

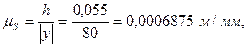
где 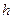- ход механизма (максимальное перемещение), м;

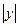- расстояние, изображающее максимальное перемещение на диаграмме, мм.

Определим масштабный коэффициент угла поворота:

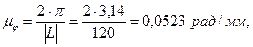
где 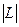- произвольно выбранное расстояние, изображающее один период работы механизма на диаграмме, мм.

Переведем все фазовые углы в масштабный коэффициент.

Фаза удаления:

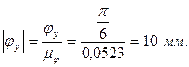
Фаза верхнего выстоя:

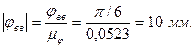
Фаза сближения:

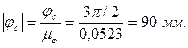
Фаза нижнего выстоя:

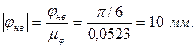
Разобьем фазовые углы удаления и сближения на шесть частей и посчитаем перемещения для каждого значения фазового угла.

Для первого положения:

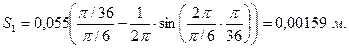
Переведем полученную величину перемещения в масштабный коэффициент:

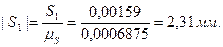
Для остальных положений расчет ведется аналогично. Результаты сведём в таблицу 9.

Таблица 9 – Значения перемещения

Фаза удаления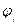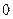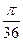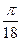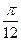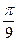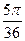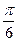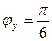
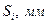		0,00159	0,0107	0,0275	0,0442	0,0534	0,055
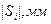		2,31	15,56		64,37	77,7
Фаза сближения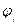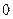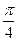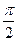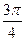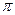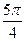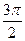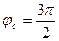
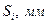		0,00159	0,0107	0,0275	0,0442	0,0534	0,055
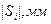		2,31	15,56		64,37	77,7

Для построения диаграммы отложим переведенные в масштабный коэффициент величины перемещений, с учетом того, что в положениях, соответствующих фазе сближения (7-13), отрезки откладываем в обратном порядке.

9.3 Функция аналога скорости

Для построения диаграммы аналога скорости воспользуемся формулой:

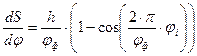
Для первого положения:

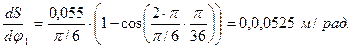
Для остальных положений аналогично, их результаты сводим в таблицу 10.

Таблица 10 – Значения скоростей

Фаза удаления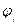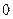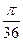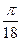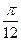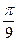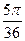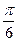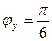
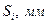		0,0525	0,1576	0,21019	0,1576	0,0525
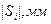		13,49	40,49		40,49	13,49
Фаза сближения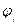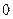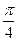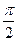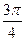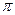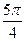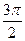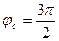
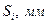		0,005838	0,0175	0,0233	0,0175	0,0058
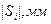		1,5	4,5		4,5	1,5

Рассчитаем масштабный коэффициент:

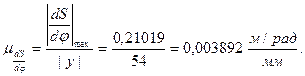
Для построения диаграммы переведем все полученные значения в масштабный коэффициент. Отложим их на диаграмме, с учетом того, что график на фазе сближения должен находиться ниже оси угла.

9.4 Функция аналога ускорения

Для построения диаграммы аналога воспользуемся формулой:

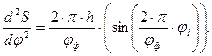
Для первого положения:

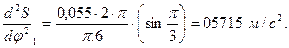
Для остальных положений вычисления проводятся аналогично. Результаты сводим в таблицу 12.

Таблица 12 – Значения ускорений

Фаза удаления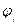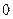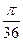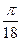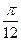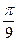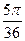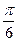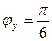
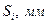		0,5715	0,5715		-0,5715	-0,5715
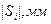Фаза сближения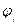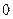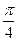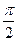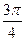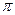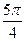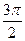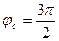
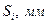		0,0635	0,0635		-0,0635	-0,0635
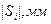		4,44	4,44		-4,44	-4,44

Рассчитаем масштабный коэффициент:

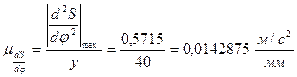
Для построения диаграммы переведем все полученные значения ускорений в масштабный коэффициент оси аналога ускорения. Отложим рассчитанные отрезки на диаграмме. В положениях фазы сближения график изображаем симметрично относительно оси угла.

9.5 Определение радиуса исходного контура. Построение диаграммы угла давления

Радиус определим из построенного треугольника, в котором один из катетов будет искомым радиусом.

Отложим отрезок 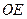длиной равной длине коромысла (85 мм). Ось перемещения S строится путем проведения из точки О дуги окружности радиусом l от точки E. Отложим по дуге, расстояния равные перемещениям. От точки 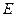через ось 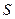проведем лучи. Возьмем значения в миллиметрах с диаграммы скорости и отложим по этим лучам отрезки (для фазы удаления в положительную, для фазы сближения в отрицательную сторону относительно оси S). Соединим все найденные точки плавной кривой и получим диаграмму для определения радиуса исходного контура кулачка.

Через третью и девятую точку диаграммы проводим прямую и строим перпендикуляр к этой прямой. Проведем две касательные к диаграмме, построенные под предельным углом давления 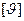от перпендикуляра в обе стороны. Таким образом мы получили область допустимых решений.

От горизонтальной линии OE под углом ( 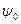) отложим луч из точки 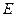, точка пересечения луча и левой касательной к диаграмме для определения радиуса исходного контура кулачка даст точку 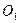. Соединив ее с точкой 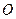, получим исходный радиус ( 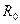), в данном случае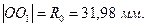

К характерным точкам диаграммы для определения радиуса исходного контура кулачка (1…13) проведем из точки 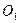прямые. От характерных точек отложим перпендикуляры и, замеряя углы, откладываем их на диаграмме углов давления в масштабном коэффициенте угла давления:

Таблица 14 – значения углов давления

№						6,7						13,14
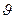	-12,4	-28,5	-28,6	-18,1	-5,6	0	0,58	2	3,5	3,4	1,4	0

9.6 Синтез профиля кулачка

Для построения теоретической окружности возьмем точку О и справа от нее, на расстоянии е, переведенное в масштабный коэффициент, проведем ось перемещение S. Проведем радиусом 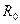окружность и поделим ее согласно данным на углы 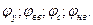По оси S отложим все перемещения.

Каждый из углов 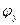и 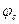поделим на шесть равных дуг и из центра окружности проведем лучи. Радиусами от точки О до 1, 2, 3и так далее по очереди будем проводить дуги до пересечения с лучом, тем самым получим профиль кулачка. Так получим теоретический профиль кулачка.

Радиус ролика найдем из выражения:

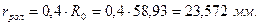
где 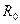- начальный радиус, мм.

Выберем стандартное целое значение из полученного ряда. Возьмем:

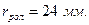
Для нахождения рабочего профиля кулачка проведем из каждой точки на теоретическом профиле окружности радиуса ролика. Соединив крайние точки этих окружностей плавной кривой получим рабочий профиль кулачка.

Список используемой литературы

1. Артоболевский, И.И. Теория механизмов и машин / И.И. Артоболевский. – М.: Наука., 1988. – 640с.

2. Попов С.А. Курсовое проектирование по теории механизмов и механике машин – Москва «Выссшая школа» 1986.

3. Теория механизмов и машин. Версия 1.0 [Электронный ресурс]: Электрон. учеб. пособие/ П.Н. Сильченко, М.А. Мерко, М.В. Меснянкин и др. – Электрон. дан. (3 Мб). – Красноярск: ИПК СФУ, 2008. – (Теория механизмов и машин: УМКД № 363-2007/ рук. творч. коллектива П.Н. Сильченко).