Изгиба пластин

В этом параграфе рассмотрим примеры вычисления элементов изгиба пластин при помощи таблиц, приведенных в § 10 и 11.

П р и м е р 1. Для свободно опертой по всему контуру прямоугольной пластины, имеющей размеры а = 100 си, b = 62,5 си, h = 0,8 см и нагруженной равномерно распределенной нагрузкой q=0,7 кг/см², определить прогиб и нормальные напряжения в ее центре, а также наибольшие реакции опорных кромок.

Прогиб, изгибающие моменты в центре пластины, а также реакции опорных кромок определяются формулами [см. формулы (226), (227), (229)]

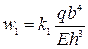
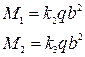
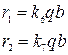
Поскольку для рассматриваемой пластины 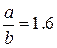, то по табл. 6 находим k₁=0,0906; k₂=0,0493; k₃=0,0862; k₆=0,303; k₇=0,491.

Следовательно,

w₁= 0,0906*0.7*62.5⁴/2*10⁶*0.8³ = 0,94 см;

М₁=0,0493*0,7*62,5²= 135 кг;

М₂=0,0862*0,7*62,5²= 236 кг;

г₁=0,303*0,7*62,5= 13,2 кг/см;

г₂=0,491*0,7*62,5=21,5 кг/см.

Для вычисления нормальных напряжений следует соответствующий изгибающий момент разделить на момент сопротивления единицы ширины сечения пластины, т. е. на .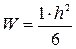

Таким образом, нормальные напряжения в центре пластины в сечении, перпендикулярном длинной кромке (оси ох),

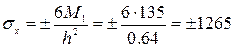кг/см²

Нормальные напряжения в центре пластины в сечении, перпендикулярном короткой кромке (оси оу),

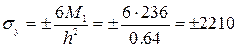кг/см²

П р и м е р 2. Прямоугольная пластина, имеющая размеры а=150 см; b=50 см; h=1,0 см, жестко заделана на длинных кромках и свободно оперта на коротких, загружена равномерно распределенной нагрузкой интенсивностью q = 0,8 кг/см². Найти нормальные напряжения по середине жестко заделанных кромок, а также наибольшие нормальные напряжения и стрелку прогиба в центре пластины (рис. 32).

Необходимые элементы изгиба определяются формулами [см. формулы (237), (238) и (239) при а>b]

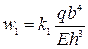
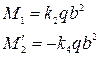
Для рассматриваемой пластины длина жестко заделанных кромок больше, чем свободно опертых, поэтому коэффициенты должны определяться по столбцам правой части табл.7.

Следует отметить, что уже при отношении 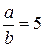коэффициенты k_i могут быть взяты такие же, что и для 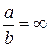. Для заданного отношения сторон 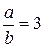необходимые коэффициенты k_i можно определить линейной интерполяцией между их значениями для 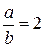и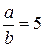

Находим k₁ = 0,0284, k₂= 0,0420; k₄=+0,0839. Следовательно,

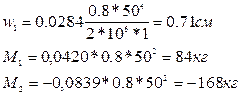
Нормальные напряжения в заделке

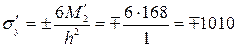кг/см²

Наибольшие нормальные напряжения в центре пластины (в сечении, перпендикулярном оси оу)

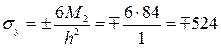кг/см²

П р и м е р 3. Найти стрелку прогиба и наибольшие нормальные напряжения в центре, а также нормальные напряжения по середине заделанных кромок для пластины, у которой длина жестко заделанных кромок а = 50 см; длина свободно опертых кромок b= 150 см, толщина h= 1,0 см . Интенсивность нагрузки q=0,8 кг/см² (рис. 32).

Необходимые элементы изгиба опрёделяются формулами [см. формулы (237), (238), (239) при а<b]

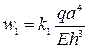
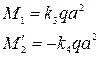
Для рассматриваемой пластины коэффициенты должны определяться по столбцам левой части табл. 7.

Находим по отношению 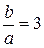; k₁=0,1276; k₈=0,1144; k₄=0.1246

Таким образом получаем

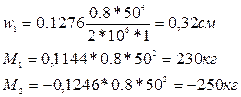
Нормальные напряжения в заделке

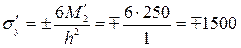кг/см²

Наибольшие нормальные напряжения в центре пластины (в сечении, перпендикулярном оси ох)

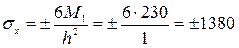кг/см²

Пример 4. Определить стрелку прогиба и нормальные напряжения в центре прямоугольной пластины, свободно опертой на все кромки и загруженной по длинной кромке постоянным изгибающим моментом интенсивностью 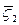= 200 кг. Размеры пластины: длинная сторона а=100 см, короткая сторона b=40 см, толщина h=0,8 см.

Искомые элементы изгиба определяются формулами (267) и (268) и табл. 8. Стрелка прогиба в центре пластины

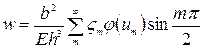
Момент в центре пластины в сечении, перпендикулярном длинной стороне (оси ох),

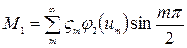
Момент в центре пластины в сечении, перпендикулярном короткой стороне (оси оу)

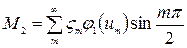
где

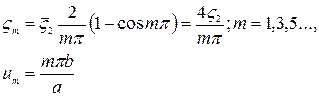
Так как для заданной пластины 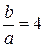, то по табл. 9 находим

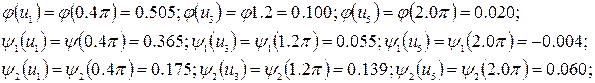
Следовательно, получим

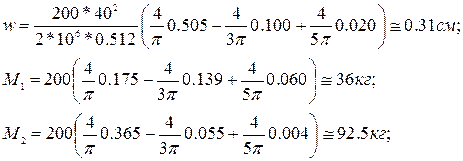
П р и м е р 5. Для прямоугольной пластины, жестко заделанной по всем кромкам и нагруженной равномерно распределенной нагрузкой интенсивностью q = 1,0 кг/см². определить наибольшие напряжения в центре пластины и на опорном контуре. Размеры пластины: а= 100 см; b==50 см; h= 1,0 см.

Наибольшие напряжения в центре пластины будут в сечении, перпендикулярном ее короткой стороне, а на опорном контуре — по середине длинной жестко заделанной кромки.

Искомые элементы изгиба определяются формулами (278) и (279) и табл. 10.

Момент в центре пластины в сечении, перпендикулярном короткой стороне (оси оу),

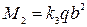
Момент по середине длинной кромки

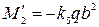
Так как для заданной пластины 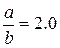, то по табл. 10 находим k3=0,0399; k₅= 0,0829.

Следовательно

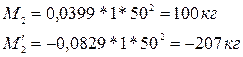
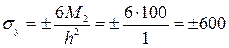кг/см²

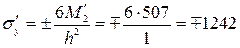кг/см²

Пример 6. Для пластины примера 5 определить нормальные напряжения в центре, направленные вдоль длинной стороны, и нормальные напряжения по середине коротких сторон опорного контура.

Искомые изгибающие моменты определяются формулам (278), (279) и табл. 10.

Момент в центре пластины в сечении, перпендикулярном длинной стороне (оси ох),

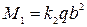
Момент по середине коротких сторон опорного контура

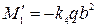
При отношении сторон пластины 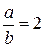коэффициент k₂ может быть вычислен по формуле k₂=0.35*k₃, а при 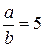k₂=0.3*k₃