Обратное z- преобразование
Лекция 8. Цифровые САУ
Основные положения и определения
Система называется цифровой, если в контуре имеется хотя бы один импульсный элемент. На рисунке 8.1 приведена цифровая САУ на базе микроконтроллера, т.е. функции сумматора и регулятора реализуются программным путем в микроконтроллере, с выхода которого сигналы поступают на объект управления с известной ПФ.
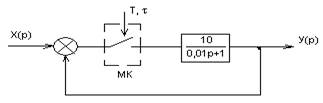
Рисунок 8.1 – Структурная схема цифровой системы
Микроконтроллер приближенно можно описать ПФ запаздывающего звена
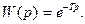
Рисунок 8.2 – Выходная характеристика запаздывающего звена
Амплитудно-импульсная модуляция (АИМ) это модуляция, при которой амплитуда импульса модулированного сигнала У пропорциональна величине информационного сигнала Х, подаваемого на вход модулятора.
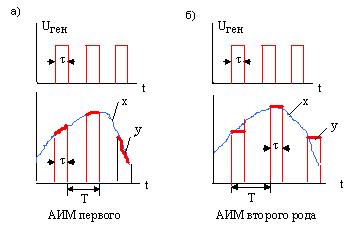
Рисунок 8.3 – Виды АИМ
Существует 2 вида АИМ: первого и второго рода. В АИМ 1-го рода амплитуда модулированного сигнала в течение длительности импульса τ повторяет информационный сигнал Х. При АИМ 2-го рода амплитуда импульса в течение длительности импульса τ постоянна. Например, в АЦП используется АИМ 2-го рода.
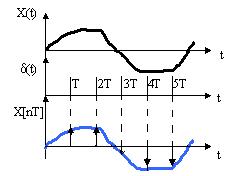
Рисунок 8.4 – Временная диаграмма работы АЦП
В АЦП преобразование происходит в 2 этапа: дискретизация по времени с периодом Т и квантование по уровню аналогового сигнала.
Поэтому блок АЦП можно представить в виде 2-х элементов: импульсного элемента, осуществляющего дискретизацию по времени и формирователя импульсов, выполняющий квантование по уровню (рисунок 8.5,а). Цифровая система (ЦС), содержащее АЦП, приведена на рисунке 8.5,б.
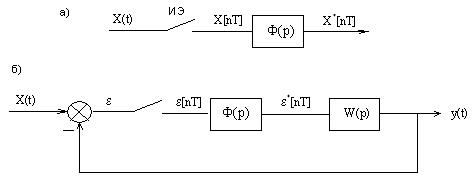
Рисунок 8.5 – Структурная схема ЦС с АЦП
При увеличении разрядности АЦП (числа квантований) ошибка между значением цифрового сигнала и аналогового уменьшается.
Таблица 8.1 - Относительные ошибки АЦП
| Число квантований | Относительная ошибка |
| 1,5 0,6 0,3 0,15 0,06 0,03 0,015 0,006 |
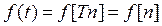
- решетчатая функция. Например, 
.
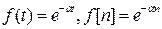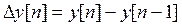- разностное уравнение 1-го порядка;
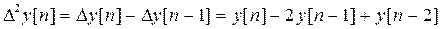- разностное уравнение 2-го порядка;
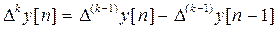- разностное уравнение k-го порядка.
Z-преобразование
Для описания ЦС используется z-преобразование. Для этого необходимо перейти из области t в область р, а затем в область Z.
Преобразование Лапласа имеет вид
.
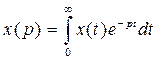Приближенно интеграл можно представить в виде суммы
.
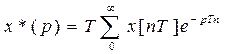Примем 
, тогда
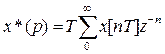или
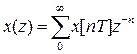. (8.1)
Пример 1. Найти z-изображение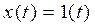 
.
.
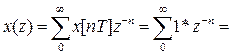
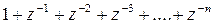В правой части уравнения сумма бесконечно убывающей геометрической прогрессии, знаменатель которой равен
.
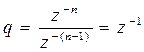Тогда
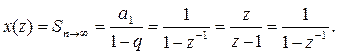
Таблица 8.2 – Примеры перехода из t в Z и P области
| F(t) | Р-преобразование | Z-преобразование |
| 1(t) t t2 exp(-at) | 1/р 1 /p2 1 /p3 1/(p+a) | z / z-1 Tz / (z-1)2 T2z(z+1) /(z-1)3 z/ (z-e-at) |
Пример 2. Дана x(t) = 1(t). Требуется получить z-изображение другим способом.
Как и при первом способе, получим изображение единичной функции в виде ряда Тейлора
x(z) = 1 + z-1 + z-2 +…..+z-n.
Умножим на z-1 обе части уравнения
x(z) ∙ z-1 = z-1 + z-2 + z-n-1,
и вычтем из первого выражения x(z), полученное x(z) ∙ z-1.
Тогда
x(z) – x(z) ∙ z-1 = 1.
Отсюда
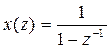
Пример 3. Дана функция x(t)= t ∙ 1(t). Получить z-изображение.
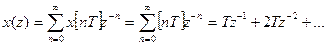
x(z) ∙ z-1 = Tz-2 + 2Tz-3 + …;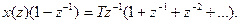 
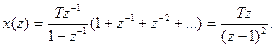
Теоремы Z- преобразования
1) Суммирование и вычитание. Если f1(t) и f2(t) имеют z-преобразование, то
.
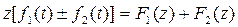2) Умножение на константу. Если f(t) имеет z- преобразование F(z), то
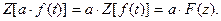
3) Сдвиг во временной области. Если f(t) имеет z- преобразование F(z), то
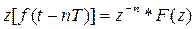
Пример 4. Найти z- преобразование единичной ступенчатой функции 1(t) при задержке ее на один период квантования Т.
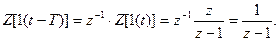
4) Об умножении оригинала на экспоненту (смещение в области изображений). Если f(t) имеет изображение f(z), то
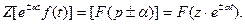
5) Теорема о начальном значении. Если f(t) имеет z- преобразование F(z) и если существует предел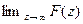 
, то
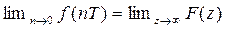
Из теоремы следует, что значение дискретного сигнала f(t) при t=0 определяется значением F(z) при z = ∞.
6) Теорема о конечном значении. Если f(t) имеет z-преобразование F(z) и если функция (1-z-1)F(z) не имеет полюсов на окружности единичного радиуса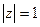 
или вне ее, то
.
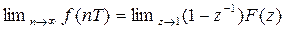Пример 5. Найти конечное значение f(nT) для заданного z-преобразования
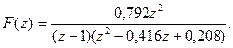
Приведем заданную функцию к виду
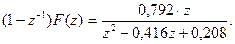
Определим корни знаменателя, т.е. определим полюса ПФ. Поскольку функция не имеет полюсов на единичной окружности, то
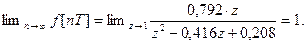
7) Теорема дифференцирования. Если z-преобразование функции f(t,a) есть F(z,a), где а – независимая переменная или константа, то
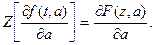
Пример 6. Определить z-преобразование функции f(t) = te-αt с помощью теоремы дифференцирования.
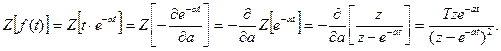
Обратное z- преобразование
Преобразование Лапласа и его обратное преобразование для непрерывных функций является однозначным. Для z-преобразования обратное z-преобразование не является однозначным. Корректный результат обратного z-преобразования функции F(z) есть f(nT), который равен f(t) только в моменты t = nT.
Рисунок 8.6 иллюстрирует тот факт, что для z-преобразования единичной ступенчатой функции, которое равно z/(z-1) и соответствует последовательности единичных импульсов. Обратное z-преобразование может быть любой функцией, значения которой равны единицы в моменты t=0,T,2T. Неоднозначность обратного z-преобразования является одним из ограничений этого метода.
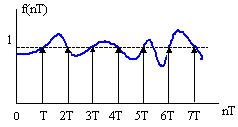
Рисунок 8.6 – Решетчатая функция ЦС
Обратное z-преобразование осуществляет переход от z-изображения к решетчатой функции и обозначается как
.
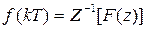Обратное z-преобразование может быть определено методом разложения на простые дроби. Этот метод близок к методу разложения на простые дроби в преобразовании Лапласа. При анализе непрерывных систем обратное преобразование Лапласа F(p) может быть получено разложением в виде
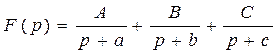, (8.2)
где а, в, с – отрицательные полюсы F(p); А, В, С – вычеты F(p) в этих полюсах.
Тогда в соответствии с таблицей 1.2 можно осуществить переход к оригиналу
.
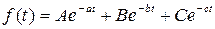Для случая z-преобразования F(z) не надо представлять в форме (8.2), поскольку в таблице 8.2 обратное z-преобразование для выражений типа A/(z + a)
отсутствует. Вместе с тем из таблицы 8.2 видно, что обратное z-преобразование функции Az/(z – e-at) равно Ae-anT.
Следовательно, удобнее разложить на простые дроби функцию F(z)/z. После разложения обе части выражения для F(z)/z умножают на z для получения F(z).
Пример 7. Дано z-изображение, имеющее вид
.
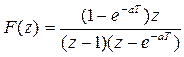Разложим по (8.2) на слагаемые
; 
.
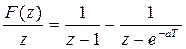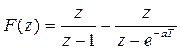В соответствии с таблицей 1.2 определяется оригинал функции
.
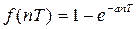