Уравнения, допускающие понижение порядка
Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка.
Уравнения вида y(n) = f(x).
Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение может быть найдено последовательным интегрированием.

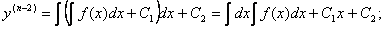
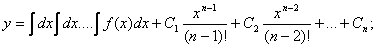
| 9.Линейные дифференциальные уравнения второго порядка |
Дифференциальное уравнение второго порядка имеет вид 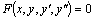 . Определение. Общим решением уравнения второго порядка называется такая функция . Определение. Общим решением уравнения второго порядка называется такая функция 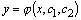 , которая при любых значениях , которая при любых значениях 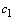 и и 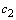 является решением этого уравнения. Определение. Линейным однородным уравнением второго порядка называется уравнение является решением этого уравнения. Определение. Линейным однородным уравнением второго порядка называется уравнение 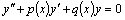 . Если коэффициенты . Если коэффициенты 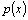 и и 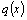 постоянны, т.е. не зависят от постоянны, т.е. не зависят от 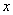 , то это уравнение называют уравнением с постоянными коэффициентами и записывают его так: , то это уравнение называют уравнением с постоянными коэффициентами и записывают его так: 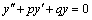 . Уравнение . Уравнение 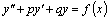 будем называть линейным неоднородным уравнением. Определение.Уравнение будем называть линейным неоднородным уравнением. Определение.Уравнение 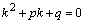 , которое получается из линейного однородного уравнения заменой функции , которое получается из линейного однородного уравнения заменой функции 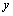 единицей, а единицей, а 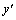 и и 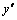 - соответствующими степенями - соответствующими степенями 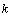 , называется характеристическим уравнением. Известно, что квадратное уравнение , называется характеристическим уравнением. Известно, что квадратное уравнение 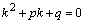 имеет решение, зависящее от дискриминанта имеет решение, зависящее от дискриминанта 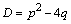 : : 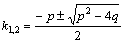  , т.е. если , т.е. если 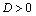 , то корни , то корни 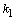 и и 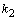 - действительные различные числа. Если - действительные различные числа. Если 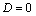 , то , то 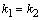 . Если же . Если же 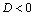 , т.е. , т.е. 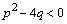 , то , то 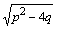 будет мнимым числом, а корни будет мнимым числом, а корни 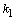 и и 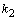 - комплексными числами. В этом случае условимся обозначать - комплексными числами. В этом случае условимся обозначать 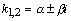 . . |
