Комплексная диэлектрическая проницаемость. Угол диэлектрических потерь

Уравнения Гельмгольца. Волновой характер эл/м поля.

Из результатов, выявленных Максвеллом, одним из главных предстало доказательство волновой природы электромагнитного поля. Как мы знаем, изменение электрического поля во времени приводит к появлению магнитного поля однородного в пространстве, и также наоборот. Здесь процесс походит на физическую картину обмена энергией между магнитным и электрическим полем в типичном колебательном контуре.

Следовательно, от этого ожидается, что в самом общем случае электромагнитный процесс представляет собой также некоторые колебания. Здесь принципиальная разница несёт в себе то, что одновременно во всех точках пространства должны рассматриваться колебания электромагнитного поля. Волновым процессом в физике принято называть колебательное движение непрерывной среды. Математически докажем волновой характер электромагнитного поля объединив уравнения Максвелла с другими уравнениями, конечно же которые описывают волновой процесс.

Проведем анализ электромагнитного поля в отдельной области пространства, там, где отсутствует плотность зарядов, то есть ρ=0. Также предполагается равной нулю плотность сторонних электрических токов.

Из системы уравнений Максвелла выпишем первые два вот в таком виде:

Для приведения этих уравнений к одному применим операцию rot к правой и левой частям второго уравнения и после через первое уравнение сформулируем полученную правую часть:

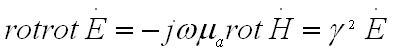
В этом месте

- при общем случае число комплексное, являющееся, постоянной распространения электромагнитной волны. Для величины γ можно встретить также в литературе наименования волновое число или фазовая постоянная. Следующую реорганизацию формулы

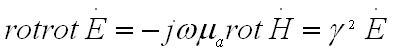
можно реализовать, если же применить известное нам тождество векторного анализа:

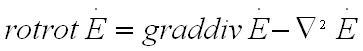
Здесь «набла квадрат» - второго порядка векторный дифференциальный оператор, конкретная форма которого определяется целиком той координатной системой, в которой ведется вычисления. Действие оператора в декартовой координатной системе сводится к тому, что используется оператор Лапласа к каждой из проекций векторного поля

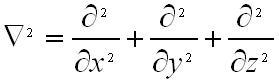
Если же использовать закон Гаусса, который обеспечивает div E=0 в соответствии с принятым условием ρ=0тогда уравнение

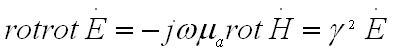
возможно будет изложить в последующем виде:

Применяя симметрию уравнений Максвелла, безусловно, аналогично также получаем уравнение сравнительно векторного поля Н;

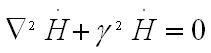
В математической физике уравнения имеют название уравнений Гельмгольца. Со стороны математики, возможно, показать, что данные уравнения описывают стационарные волновые процессы, то есть распространение волн в пространстве с отдельной хронической частотой. Тем самым принято фундаментальное заключение теории Максвелла – переменность магнитных или электрических полей во времени неминуемо ведёт к распространению электромагнитных волн в пространстве.

Энергетические соотношения в эл/м поле.

Наряду основных свойств электромагнитного поля стоит его энергия. Этот вопрос впервые был проанализирован Максвеллом, который выявил, что вся энергия поля, заключённого внутри объема V, сформировывается из энергии электрического поля

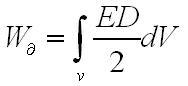
и энергии магнитного поля

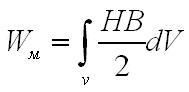
Подынтегральные выражения в выше изложенных формулах могут рассматриваться, таким образом, как плотности энергии электрического поля

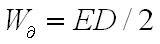
и магнитного поля

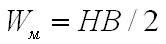
Вообще говоря, энергия электромагнитного поля, заключённого внутри объема V, не может быть постоянной. Следует отнести к числу факторов, ниже описанные явления, которые определяют изменение во времени энергии поля:

· обращение части энергии электромагнитного поля в энергию других типов, к примеру, в механическую энергию, связанную с тепловым движением частиц вещества, определённым протеканием токов проводимости;

· действия других источников, которые могут как уменьшать запас энергии поля, так и увеличивать его в зависимости от заданных условий;

· передача энергии между выделенным объемом, а также окружающими его областями пространства за счёт характерного процесса, свойственного электромагнитному полю и обладающему названием процесса излучения.