Теорема об изменении кинетической энергии точки

Рассмотрим точку с массой т, перемещающуюся под действием при­ложенных к ней сил из положения M₀ , где она имеет скорость 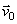, в положение М₁ , где ее скорость равна .

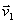Для получения искомой зависимости обратимся к уравнению 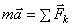выражающему основной закон динамики. Проектируя обе части этого равенства на касательную 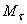к траектории точ­ки М, направленную в сторону движения, получим:

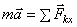
Стоящую слева величину касательного ускорения можно пред­ставить в виде

.

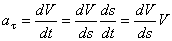В результате будем иметь:

.

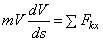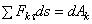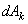Умножив обе части этого равенства на ds, внесем т под знак дифференциала. Тогда, замечая, что где - эле­ментарная работа силы F_k получим выражение теоремы об изме­нении кинетической энергии в дифференциальной форме:

.

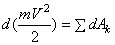Проинтегрировав теперь обе части этого равенства в пределах, соответствующих значениям переменных в точках M₀ и M₁, найдем окончательно:

.

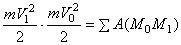Уравнение выражает теорему об изменении кине­тической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

Кинетическая энергия системы

Кинетической энергией системы называется скалярная величина Т, равная арифметиче­ской сумме кинетических энергий всех точек системы

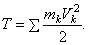
Кинетическая энергия является характеристикой и поступатель­ного и вращательного движения системы, поэтому теоремой об изме­нении кинетической энергии особенно часто пользуются при решении задач.

Если система состоит из нескольких тел, то ее кинетическая энергия равна, очевидно, сумме кинетических энергий этих тел:

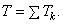
Кинетическая энергия – скалярная и всегда положительная величина.

Найдем формулы для вычисления кинетической энергии тела в разных случаях движения.

1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости дви­жения центра масс. То есть, для любой точки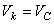

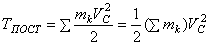
или

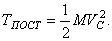
Таким образом, кинетическая энергия тела при поступатель­ном движении равна половине произведения массы тела на квад­рат скорости центра масс. От направления движения значение Т не зависит.

2. Вращательное движение. Если тело вращается вокруг какой-нибудь оси Оz (см. рис.46), то скорость любой его точки 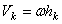, где 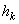- расстояние точки от оси вращения, а - угло­вая скорость тела. Подставляя это значение и вынося общие множители за скобку, получим:

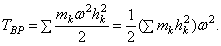
Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Таким образом, окончательно найдем:

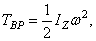
т. е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение Т не зависит.

3. Плоскопараллельное движение. При этом движе­нии скорости всех точек тела в каждый момент времени распреде­лены так, как если бы тело вращалось вокруг оси, перпендикулярной к плоскости движения и проходящей через мгновенный центр ско­ростей Р (рис.46). Следовательно

,

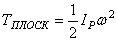где 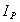- момент инерции тела относительно названной выше оси, - угловая скорость тела. Величина 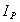в формуле будет перемен­ной, так как положение центра Р при движе­нии тела все время меняется. Введем вместо 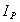постоянный момент инерции 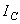, относительно оси, проходящей через центр масс С тела. По теореме Гюйгенса 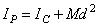, где d=PC. Подставим это выражение для 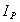. Учитывая, что точка Р - мгновенный центр скоростей, и, следовательно, 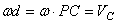, где 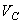- скорость центра масс С, окончательно найдем:

.

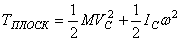Следовательно, при плоскопараллельном движении кинетиче­ская энергия тела равна энергии поступательного движения со скоростью центра масс, сло­женной скинетической энергией вращательного движения вокруг центра масс.

4) Для самого общего случая движения материальной системы кинетическую энергию помогает вычислить теорема Кенига.

Рассмотрим движение материальной системы как сумму двух движений (рис.48). Переносного – поступательного движения вместе с центром масс С и относительного – движения относительно поступательно движущихся вместе с центром масс осей x₁, y₁, z_1. Тогда скорость точек 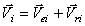. Но переносное движение – поступательное. Поэтому переносные скорости всех точек равны, равны 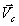. Значит, 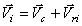и кинетическая энергия будет

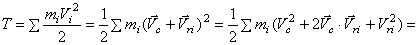
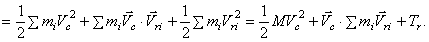
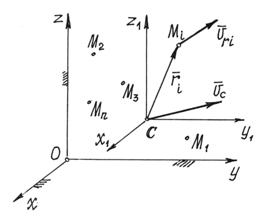
Рис.48

По определению центра масс его радиус-вектор в подвижной системе 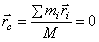(центр масс находится в начале координат), значит, и 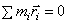. Производная по времени от этой суммы также равна нулю:

.

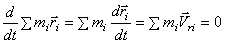Поэтому, окончательно, кинетическая энергия системы

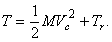(1)

Кинетическая энергия материальной системы равна сумме кинетической энергии при поступательном движении вместе с центром масс и кинетической энергии ее при движении относительно координатных осей, поступательно движущихся вместе с центром масс.

В общем случае движения тела, которое можно рассматривать как сумму двух движений (переносного – поступательного вместе с центром масс С и относительного – вращения вокруг точки С), по теореме Кенига (1) получим

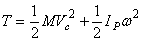или ,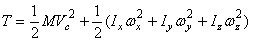

где I_x, I_y, I_z – главные центральные оси инерции тела.