Задания для самостоятельной работы. 1. Одним и тем же прибором со средним квадратическим отклонением случайных ошибок измерений произведено пять равноточных измерений расстояния от орудия до
1. Одним и тем же прибором со средним квадратическим отклонением случайных ошибок измерений 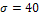 произведено пять равноточных измерений расстояния от орудия до цели. Найти доверительный интервал для оценки истинного расстояния
произведено пять равноточных измерений расстояния от орудия до цели. Найти доверительный интервал для оценки истинного расстояния 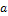 до цели с надежностью
до цели с надежностью 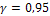 зная среднее арифметическое результатов измерений
зная среднее арифметическое результатов измерений 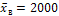 м. Предполагается, что результаты измерений распределены нормально.
м. Предполагается, что результаты измерений распределены нормально.
2. Найти доверительный интервал для оценки математического ожидания 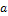 нормального распределения с надежностью 0.95, зная выборочную среднюю
нормального распределения с надежностью 0.95, зная выборочную среднюю 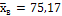 объем выборки
объем выборки 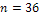 и среднее квадратическое отклонение
и среднее квадратическое отклонение 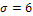 . Полученный доверительный интервал изобразить графически.
. Полученный доверительный интервал изобразить графически.
3. Даны выборочные варианты 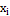 и соответствующие им частоты
и соответствующие им частоты 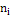 количественного признака
количественного признака 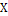 .
.
а) Найти выборочные среднюю, дисперсию и среднее квадратическое отклонение
б) Считая, что количественный признак X распределен по нормальному закону и что выборочная дисперсия равна генеральной дисперсии, найти доверительный интервал для оценки математического ожидания с надежностью 0.95.

Вопросы для самоконтроля:
1. В чём состоит сущность выборочного метода?
2. Как записать результаты выборки?
3. Назовите основные характеристики выборочного распределения.
4. Как вычисляется выборочная средняя?
5. Выборочная дисперсия и среднее квадратическое отклонение. В чём заключается смысл этих характеристик?
6. Способы вычисления дисперсии.
7. Как оценить генеральную среднюю признака?
8. Для чего служит доверительный интервал?
9. Как вычислить длину доверительного полуинтервала? От чего зависит эта длина?
