Тема 4: Линейное уравнение множественной регрессии

1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х₁) и уровня безработицы в субъекте (%, х₂) получено уравнение 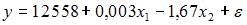. Величина коэффициента регрессии при переменной х₂ свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.

изменится на (-1,67)

увеличится на 1,67

уменьшится на (-1,67)

изменится на 0,003

Решение:

Эконометрическая модель линейного уравнения регрессии имеет вид 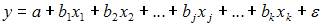, где y – зависимая переменная, x_j – независимая переменная ( 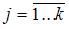– номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, b_j – параметры уравнения; 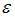– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Коэффициентом регрессии является параметр b_j. Его величина показывает, на сколько в среднем изменится зависимая переменная y, при изменении соответствующей независимой переменной x_j на 1 единицу измерения. Таким образом, при изменении уровня безработицы на 1% среднедушевой денежный доход изменится на (-1,67) рубля при неизменной величине валового регионального продукта.

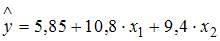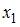2. В уравнении линейной множественной регрессии: , где – стоимость основных фондов (тыс. руб.); 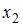– численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х₁, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.

на 1 тыс. руб. … увеличится на 10,8 тыс. руб.

на 1 тыс. руб. … уменьшится на 10,8 тыс. руб

на 1 тыс. руб. … увеличится на 10,8%

на 1% … увеличится на 10,8%

Решение:

В уравнении множественной линейной регрессии 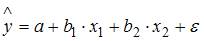, параметр 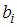показывает среднее изменение результата y при увеличении фактора 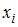на одну единицу, при условии, что все остальные переменные останутся на постоянном уровне. В нашем случае, объем промышленного производства y характеризуется следующим уравнением 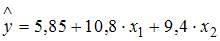, параметр 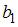равен 10,8, следовательно, при увеличении объема основных фондов на 1 тыс. руб. объем промышленного производства увеличится на 10,8 тыс. руб. при постоянной численности занятых.

3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …

0,8

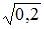
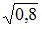
0,64

Решение:

Коэффициент детерминации 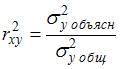равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина ( 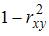) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
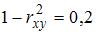. Значит,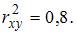

4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х₁): 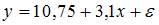. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.

10,75

3,1

13,85

7,65

Решение:

Эконометрическая модель линейного уравнения парной регрессии имеет вид: 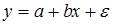, где y – зависимая переменная, x – независимая переменная; a, b – параметры уравнения; 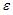– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Значение параметра а может быть рассчитано по формуле 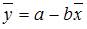. Если 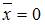, то 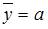; в таком случае говорят, что среднее значение переменной y, не зависящее от величины переменной х, равно значению параметра а. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет 10,75 рубля.

5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы.

факторной … остаточной

остаточной … факторной

факторной … к общей

остаточной … общей

Решение:

F-статистика рассчитывается как отношение факторной дисперсии на одну степень свободы к остаточной дисперсии на одну степень свободы.

Тема 5: Оценка параметров линейных уравнений регрессии

Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.

разность

сумма квадратов разности

квадрат разности

сумма разности квадратов

Решение:

Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения 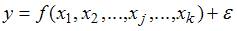, где y – зависимая переменная; x_j – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция); 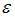– случайные факторы. При этом 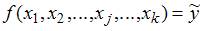, тогда 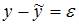, где 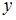– фактическое значение зависимой переменной, 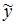– расчетное значение зависимой переменной, 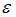– ошибка модели. Выразим значение 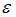: 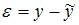. Поэтому правильный ответ – «разность».

2. Величина 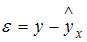называется …

случайной составляющей

оценкой параметра

значением параметра

переменной

Решение:

Величина 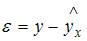называется случайной составляющей, или возмущением, и включает в себя влияние факторов, неучтенных в модели, ошибок выборки и ошибок измерения.

3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …

ошибку модели

величину коэффициента регрессии

значение свободного члена уравнения

нулевое значение независимой переменной

Решение:

Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения 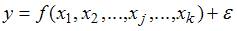, где y – зависимая переменная; x_j – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция); 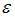– случайные факторы. При этом 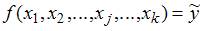, тогда 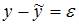, где 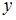– фактическое значение зависимой переменной, 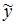– расчетное значение зависимой переменной, 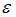– ошибка модели. Поэтому правильный ответ – «ошибку модели».

4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …

0,2

0,8

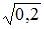
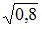
Решение:

Коэффициент детерминации 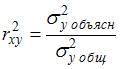равен доле дисперсии, объясненной регрессией, в общей дисперсии. Следовательно,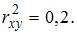

5. При методе наименьших квадратов параметры уравнения парной линейной регрессии 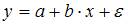определяются из условия ______ остатков .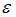