Отбор факторов в модель линейной множественной регрессии

Включаемые во множественную регрессию факторы должны объяснить вариацию зависимой переменной. Если строится модель с набором m факторов, то для нее рассчитывается коэффициент детерминации 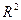, который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии m факторов. Влияние других, не учтенных в модели факторов, оценивается как 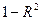с соответствующей остаточной дисперсией .

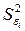При дополнительном включении в регрессию m+1 фактора коэффициент детерминации должен возрастать, а остаточная дисперсия 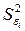уменьшаться:

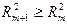и .

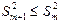Если же этого не происходит и данные показатели практически не отличаются друг от друга, то включаемый в анализ фактор x_m+1 не улучшает модель и практически является лишним фактором.

Хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа. Отбор факторов в модель линейной регрессии обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей линейной корреляции определяют статистики для параметров регрессии.

Коэффициенты интеркорреляции (т.е. линейной корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если 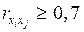. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.

Пусть, например, при изучении некоторой зависимости матрица парных коэффициентов корреляции оказалась следующей:

	y	x1	x2	x3
y		0,8	0,7	0,6
x1	0,8		0,8	0,5
x2	0,7	0,8		0,2
x3	0,6	0,5	0,2

Таблица 4.1

Очевидно, что факторы x₁ и x₂ 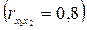дублируют друг друга. В анализ целесообразно включить фактор x₂, а не x₁, хотя корреляция x₂ с результатом 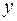слабее, чем корреляция фактора x₁ с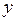 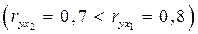, но зато значительно слабее межфакторная корреляция 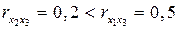. Поэтому в данном случае в уравнение множественной регрессии включаются факторы x₂, x₂.

Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности.

Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий: 1. затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл; 2. оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов линейной корреляции между факторами.

Если бы факторы не коррелировали между собой, то матрица парных линейных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы 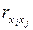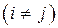были бы равны нулю. Так, для уравнения линейной регрессии, включающего три объясняющих переменных

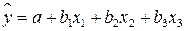(4.1)

матрица коэффициентов корреляции между факторами имела бы определитель, равный единице:

.

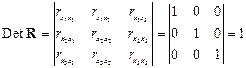Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю:

.

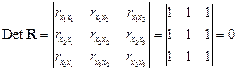Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними.

Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т.е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Так, если 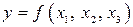, то возможно построение следующего совмещенного уравнения:

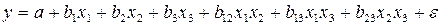. (4.2)

Рассматриваемое уравнение включает взаимодействие первого порядка (взаимодействие двух факторов). Возможно включение в модель и взаимодействий более высокого порядка, если будет доказана их статистическая значимость по 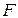-критерию Фишера, но, как правило, взаимодействия третьего и более высоких порядков оказываются статистически незначимыми.