Уравнения напряжений трансформатора
Основной переменный магнитный поток Ф в магнитопроводе трансформатора, сцепляясь с витками обмоток w1 и w2 (см. рис. 1.1), наводит в них ЭДС [см. (1.1) и (1.2)]
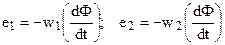 .
.
Предположим, что магнитный поток Ф является синусоидальной функцией времени, т. е.
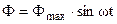 , (1.4)
, (1.4)
где Фmax – максимальное значение потока.
Тогда, подставив (1.4) в формулу ЭДС e1 и дифференцируя, получим
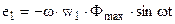 . (1.5)
. (1.5)
Но так как 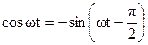 , то
, то
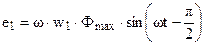 . (1.6)
. (1.6)
По аналогии,
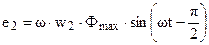 . (1.7)
. (1.7)
Из (1.6) и (1.7) следует, что ЭДС e1 и е2 отстают по фазе от потока Ф на угол 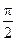 . Максимальное значение ЭДС
. Максимальное значение ЭДС
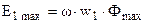 . (1.8)
. (1.8)
Разделив 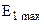 на
на 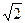 и подставив
и подставив 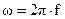 , получим действующее значение первичной ЭДС (В):
, получим действующее значение первичной ЭДС (В):
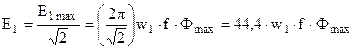 . (1.9)
. (1.9)
Аналогично, для вторичной ЭДС
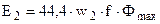 . (1.10)
. (1.10)
Отношение ЭДС обмотки высшего напряжения к ЭДС обмотки низшего напряжения называют коэффициентом трансформации:
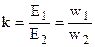 . (1.11)
. (1.11)
При практических расчетах коэффициент трансформации с некоторым допущением принимают равным отношению номинальных напряжений обмоток ВН и НН: 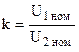 .
.
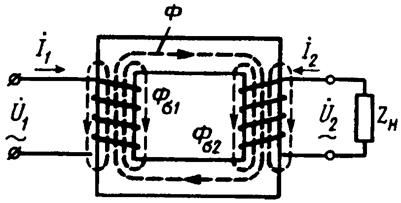
Рис. 30. Магнитные потоки в однофазном трансформаторе
Токи I1 и I2 в обмотках трансформатора помимо основного магнитного потока Ф создают магнитные потоки рассеяния Фσ1 и Фσ2 (рис. 30), каждый из которых сцеплен с витками лишь собственной обмотки и индуцирует в ней ЭДС рассеяния. Эти ЭДС в первичной и вторичной обмотках таковы:
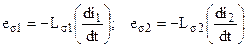 ,
,
где Lσ1 и Lσ2 – индуктивности рассеяния.
Так как магнитные потоки рассеяния замыкаются главным образом в немагнитной среде (воздух, масло, медь), магнитная проницаемость которой постоянна, то и индуктивности Lσ1 и Lσ2 можно считать постоянными.
Действующие значения ЭДС рассеяния пропорциональны токам в соответствующих обмотках:
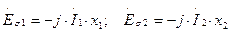 , (1.12)
, (1.12)
где х1 и х2 – индуктивные сопротивления рассеяния первичной и вторичной обмоток соответственно, Ом (знак минус в этих выражениях свидетельствует о реактивности ЭДС рассеяния).
Таким образом, в каждой из обмоток трансформатора индуцируются пв две ЭДС: ЭДС от основного потока Ф и ЭДС от потока рассеяния (Фσ1 в первичной обмотке и Фσ2 во вторичной обмотке).
Для первичной цепи трансформатора, включенной в сеть на напряжение U1, с учетом падения напряжения в активном сопротивлении первичной обмотки r1 можно записать уравнение напряжений по второму закону Кирхгофа:
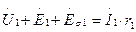
или, перенеся ЭДС 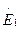 и
и 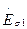 в правую часть уравнения и выразив ЭДС рассеяния через индуктивное сопротивление рассеяния х1, получим уравнение напряжений для первичной цепи трансформатора:
в правую часть уравнения и выразив ЭДС рассеяния через индуктивное сопротивление рассеяния х1, получим уравнение напряжений для первичной цепи трансформатора:
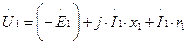 . (1.13)
. (1.13)
ЭДС первичной обмотки Е1, наведенная основным магнитным потоком Ф, представляет собой ЭДС самоиндукции, а поэтому находится в противофазе с подведенным к первичной обмотке напряжением U1.
Обычно индуктивное 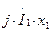 и активное
и активное 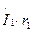 , падения напряжения невелики, а поэтому с некоторым приближением можно считать, что подведенное к трансформатору напряжение U1 уравновешивается ЭДС Е1, т. е.
, падения напряжения невелики, а поэтому с некоторым приближением можно считать, что подведенное к трансформатору напряжение U1 уравновешивается ЭДС Е1, т. е.
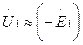 . (1.14)
. (1.14)
Для вторичной цепи трансформатора, замкнутой на нагрузку с сопротивлением ZH, уравнение напряжений имеет вид
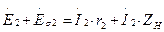 , (1.15)
, (1.15)
т.е. сумма ЭДС, наведенных во вторичной обмотке 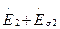 , уравновешивается суммой падений напряжений
, уравновешивается суммой падений напряжений 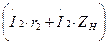 . Здесь r2 – активное сопротивление вторичной обмотки. Падение напряжения на нагрузке
. Здесь r2 – активное сопротивление вторичной обмотки. Падение напряжения на нагрузке 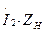 представляет собой напряжение на выводах вторичной обмотки трансформатора:
представляет собой напряжение на выводах вторичной обмотки трансформатора:
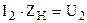 . (1.16)
. (1.16)
Приведем уравнение (1.15) к виду, аналогичному уравнению ЭДС для первичной цепи (1.13). При этом учтем выражения (1.12) и (1.16) и получим уравнение напряжений для вторичной цепи трансформатора:
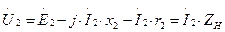 . (1.17)
. (1.17)
Из этого уравнения следует, что напряжение на выходе нагруженного трансформатора отличается от ЭДС вторичной обмотки на величину падения напряжений в этой обмотке.
Трансформатор работает в режиме холостого хода (рис. 31, а), если к зажимам его первичной обмотки подведено напряжение U1, а вторичная обмотка разомкнута (I2 = 0). Ток I0 в первичной обмотке при этих условиях называют током холостого хода.
Магнитодвижущая сила (МДС) I0w1, созданная этим током, наводит в магнитопроводе трансформатора основной магнитный поток, максимальное значение которого
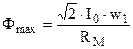 , (1.18)
, (1.18)
где RМ – магнитное сопротивление магнитопровода.
При замыкании вторичной обмотки на нагрузку ZН (рис. 31, б) в ней возникает ток I2. При этом ток в первичной обмотке увеличивается до значения I1.
Теперь поток Фmax создается действиями МДС I1w1 и I2w2:
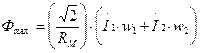 . (1.19)
. (1.19)
Этот поток можно определить из (1.9):
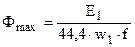
или, принимая во внимание, что 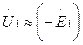 , получим
, получим
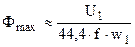 . (1.20)
. (1.20)
Из (1.20) следует, что значение основного магнитного потока Ф практически не зависит от нагрузки трансформатора, так как напряжение U1 неизменно. Однако следует иметь в виду, что это положение является приближенным и относится к случаям нагрузки, не превышающим номинальную. Объясняется это тем, что положение о неизменности потока Ф принято на основании уравнения 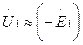 , которое не учитывает падений напряжения в первичной цепи [сравните с (1.13)].
, которое не учитывает падений напряжения в первичной цепи [сравните с (1.13)].
Принятое положение Ф = const позволяет приравнять выражения (1.18) и (1.19):
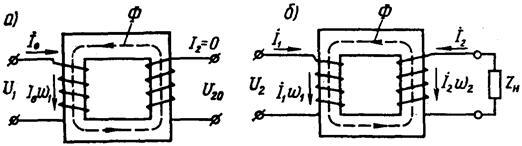
Рис. 31. Режимы холостого хода (а) и нагрузки (б)
в однофазном трансформаторе
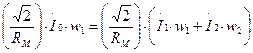
и получить уравнение МДС трансформатора:
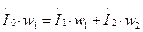 . (1.21)
. (1.21)
Преобразуя (1.21), можно МДС первичной обмотки 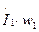 представить в виде суммы двух составляющих:
представить в виде суммы двух составляющих:
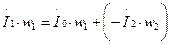 .
.
Составляющая 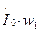 наводит в магнитопроводе трансформатора основной магнитный поток Ф, а составляющая
наводит в магнитопроводе трансформатора основной магнитный поток Ф, а составляющая 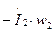 уравновешивает МДС вторичной обмотки
уравновешивает МДС вторичной обмотки 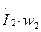 .
.
Разделив уравнение МДС (1.21) на число витков w1 получим
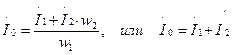 , (1.23)
, (1.23)
где 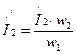 – ток нагрузки (вторичный ток), приведенный к числу витков первичной обмотки.
– ток нагрузки (вторичный ток), приведенный к числу витков первичной обмотки.
Преобразовав выражение (1.23), получим уравнение токов трансформатора:
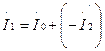 . (1.24)
. (1.24)
Из этого уравнения следует, что первичный ток I1 можно рассматривать как сумму двух составляющих: составляющую I0, создающую МДС I0w1, необходимую для наведения в магнитопроводе основного магнитного потока Ф, и составляющую 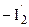 , которая, создавая МДС
, которая, создавая МДС 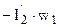 , компенсирует МДС вторичной обмотки I2w2 трансформатора. Такое действие составляющих первичного тока приводит к тому, что любое изменение тока нагрузки I2 сопровождается изменением первичного тока I1 за счет изменения его составляющей
, компенсирует МДС вторичной обмотки I2w2 трансформатора. Такое действие составляющих первичного тока приводит к тому, что любое изменение тока нагрузки I2 сопровождается изменением первичного тока I1 за счет изменения его составляющей 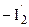 , находящейся в противофазе с током нагрузки I2.
, находящейся в противофазе с током нагрузки I2.
Основной магнитный поток Ф является переменным, а поэтому магнитопровод трансформатора подвержен систематическому перемагничиванию. Вследствие этого в магнитопроводе трансформатора имеют место магнитные потери от гистерезиса и вихревых токов, наводимых переменным магнитным потоком в пластинах электротехнической стали. Мощность магнитных потерь эквивалентна активной составляющей тока х.х. Таким образом, ток х.х. имеет две составляющие: реактивную I0р, представляющую собой намагничивающий ток, и активную I0а, обусловленную магнитными потерями:
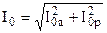 . (1.25)
. (1.25)
Обычно активная составляющая тока х.х. невелика и не превышает 0,10 от I0, поэтому она не оказывает заметного влияния на ток х.х.
На рис. 32, представлена векторная диаграмма, на которой показаны векторы тока х.х. 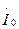 и его составляющих
и его составляющих 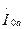 и
и 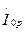 . Угол δ, на который вектор основного магнитного потока Фmax отстает по фазе от тока
. Угол δ, на который вектор основного магнитного потока Фmax отстает по фазе от тока 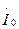 , называют углом магнитных потерь. Нетрудно заметить, что этот угол увеличивается с ростом активной составляющей тока х.х. I0a, т. е. с ростом магнитных потерь в магнитопроводе трансформатора.
, называют углом магнитных потерь. Нетрудно заметить, что этот угол увеличивается с ростом активной составляющей тока х.х. I0a, т. е. с ростом магнитных потерь в магнитопроводе трансформатора.
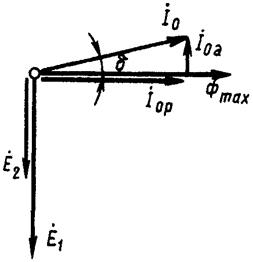
Рис. 32. Разложение тока х.х. на составляющие
Сила тока х.х. в трансформаторах большой и средней мощности соответственно составляет 2–10% от номинального первичного тока. Поэтому при нагрузке, близкой к номинальной, пренебрегая током I0 и преобразуя (1.22), получим
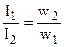 , (1.26)
, (1.26)
т. е. токи в обмотках трансформатора обратно пропорциональны числам витков этих обмоток: ток больше в обмотке с меньшим числом витков и меньше в обмотке с большим числом витков. Поэтому обмотки НН выполняют проводом большего сечения, чем обмотки ВН, имеющие большее число витков.
