Запаздывающие потенциалы
Пусть в некотором объеме 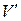 совершает движение системы зарядов, распределение и движение, которых характеризуется заданными функциями
совершает движение системы зарядов, распределение и движение, которых характеризуется заданными функциями 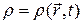 и
и 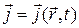 координат и времени
координат и времени 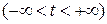 .
.
В случае калибровки Лоренца:
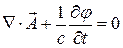 (1)
(1)
Уравнения для потенциалов электромагнитного поля 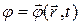 и
и 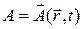 имеют вид:
имеют вид:
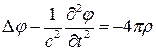 (2)
(2)
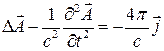 (3)
(3)
Для однозначного решения системы уравнений (1) – (3) известных функций необходимо задать начальные и граничные условия для A и φ.
Обычно задача формулируется так: до некоторого начального момента времени t=0 (t<0) заряды неподвижны, а начиная с момента времени t=0 при t>0 приходят в движение. При этом в электромагнитном поле возникает изменение (возбуждение). Будем полагать, что в (1) – (3) фигурируют потенциалы именно возмущенного поля. Функции 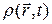 ,
, 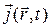 ответственные за возмущение поля при t>0 считается известными. При
ответственные за возмущение поля при t>0 считается известными. При 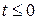 следует положить:
следует положить:
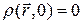 ,
,  .
.
Соответственно, 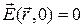 ,
, 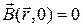 . Тогда начальные условия для потенциалов таков:
. Тогда начальные условия для потенциалов таков:
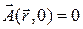 ,
, 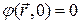 ,
, 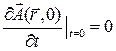 (4)
(4)
Из определения 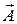 и
и 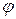 видно, что при этом векторы поля действительно равны нулю.
видно, что при этом векторы поля действительно равны нулю.
В качестве граничных условий выбирают обычно условия
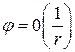 ,
, 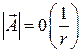 при
при 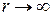 ,
, 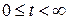 (5)
(5)
Т.е. 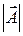 и
и 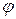 должны убывать на медленнее функции
должны убывать на медленнее функции 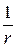 при
при 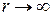 .
.
Для решения системы (1) – (3) воспользуемся простым хотя и не строгим методом, основанном на принципе суперпозиции.
Разобьем систему на совокупность сколь угодно малых зарядов 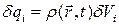 , где
, где 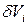 - сколь угодно малый объём в
- сколь угодно малый объём в 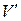 . Найдём потенциалы поля, создаваемые зарядом
. Найдём потенциалы поля, создаваемые зарядом 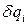 в точке наблюдения, считается что никаких других зарядов в пространстве нет. Полное же поле найдем суммируя поля, создаваемое всеми зарядами
в точке наблюдения, считается что никаких других зарядов в пространстве нет. Полное же поле найдем суммируя поля, создаваемое всеми зарядами 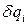 системы. Кажущееся нарушения закона сохранения заряда – не существуют уединенные переменные во времени заряда – не отразится на конечном решении, в котором будет проведено суммирование ко всем зарядам систем.
системы. Кажущееся нарушения закона сохранения заряда – не существуют уединенные переменные во времени заряда – не отразится на конечном решении, в котором будет проведено суммирование ко всем зарядам систем.
Найдем сначала потенциалы поля, создаваемые зарядами 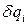 вне объема
вне объема 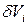 . Уравнения (1) – (3) примут вид:
. Уравнения (1) – (3) примут вид:
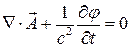
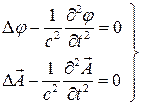 (6)
(6)
Введем сферические координаты с началом в объеме 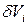 . Поле вне объема
. Поле вне объема 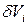 имеет сферическую симметрию и зависит только от расстояния до точки наблюдения r. В сферических координатах (6) имеют вид
имеет сферическую симметрию и зависит только от расстояния до точки наблюдения r. В сферических координатах (6) имеют вид
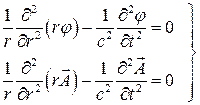 (7)
(7)
Т.е. 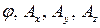 определяются уравнением одного вида
определяются уравнением одного вида
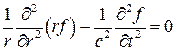 (8)
(8)
которое называют волновым уравнением.
Будем решать его методом Даламбера.
Перепишем (8) в виде:
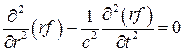
или
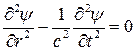 (9)
(9)
где 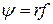 (10)
(10)
Перейдем в (9) к новым переменным
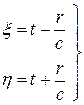 (11)
(11)
Откуда
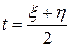 ,
, 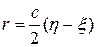 (12)
(12)
так, что
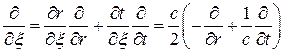
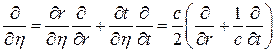
Следовательно
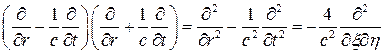 (13)
(13)
Итак, в новых переменных уравнение (9) имеет вид
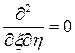 (14)
(14)
и интегрируется непосредственно. Оно удовлетворяется любыми функциями 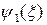 и
и 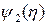 одной переменой
одной переменой 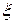 либо
либо 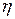 . Поэтому общее решение можно записать в следующем виде
. Поэтому общее решение можно записать в следующем виде
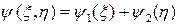
или, возвращаясь к старым переменным,
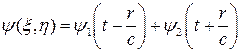 (15)
(15)
Это решение имеет простой смысл. Значение 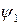 в точке
в точке 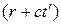 в момент времени
в момент времени 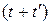 совпадает со значением
совпадает со значением 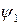 в точке r в момент времени t. Таким образом
в точке r в момент времени t. Таким образом 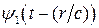 описывает периодический во времени и пространстве процесс – волновой процесс. При этом волна распространяется в сторону возрастающих значений r со скоростью c. Аналогично
описывает периодический во времени и пространстве процесс – волновой процесс. При этом волна распространяется в сторону возрастающих значений r со скоростью c. Аналогично 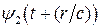 описывает волну идущую от больших r к меньшим. Для функции
описывает волну идущую от больших r к меньшим. Для функции 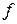 имеем
имеем
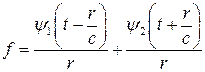 (16)
(16)
Следовательно, общее решение уравнения (8) описывает наложения двух волн - сходящихся и расходящихся. Поверхности сфер 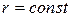 являются поверхностями постоянного значения
являются поверхностями постоянного значения 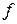 или поверхностями равной фазы. Поэтому говорят, что
или поверхностями равной фазы. Поэтому говорят, что 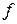 описывает волновой процесс, который является совокупностью сходящейся и расходящейся сферических волн.
описывает волновой процесс, который является совокупностью сходящейся и расходящейся сферических волн.
Любые из величин 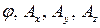 можно представить в виде (16). Рассмотрим одно из частных решений, например, сходящуюся волну. Для скалярного потенциала будем иметь
можно представить в виде (16). Рассмотрим одно из частных решений, например, сходящуюся волну. Для скалярного потенциала будем иметь
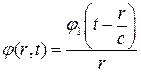 (17)
(17)
Вне объёма 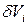 (17) справедливо любое
(17) справедливо любое 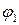 .Потребуем чтобы (17) непрерывно переходило в решение исходного уравнения (2) вблизи объёма
.Потребуем чтобы (17) непрерывно переходило в решение исходного уравнения (2) вблизи объёма 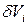 (вблизи точки расположения заряда
(вблизи точки расположения заряда 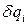 ).
).
Если в (2) совершить формальный переход 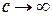 , то оно превратиться в уравнение для электростатического потенциала, решением для которого служит
, то оно превратиться в уравнение для электростатического потенциала, решением для которого служит
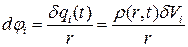 (18)
(18)
Поэтому, записав (17) в виде
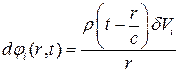 (19)
(19)
мы получим выражение для потенциала поля, создаваемого зарядом 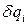 , которое удовлетворяет уравнению (7) и переходит вблизи начала координат в (18).
, которое удовлетворяет уравнению (7) и переходит вблизи начала координат в (18).
Формула (19) показывает, что потенциальное поле в точке, находящееся в момент времени t на расстоянии r от начала координат, определяется значением заряда в предшествующий момент времени 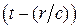 . Поэтому потенциал (19) называют запаздывающим потенциалом, а величину
. Поэтому потенциал (19) называют запаздывающим потенциалом, а величину 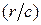 - временем запаздывания. Это время, за которое распространяющееся со скоростью с электрическое поле проходит путь r.
- временем запаздывания. Это время, за которое распространяющееся со скоростью с электрическое поле проходит путь r.
Вводя начало координат в некоторой точке О, расположенную в объёме 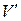 и синтезируя по всем зарядам системы получим следующее выражение для потенциала поля в точке наблюдения
и синтезируя по всем зарядам системы получим следующее выражение для потенциала поля в точке наблюдения
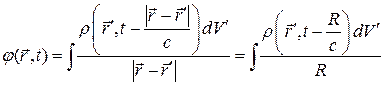 (20)
(20)
где 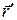 - переменная интегрирования( место положительного элементарного объёма
- переменная интегрирования( место положительного элементарного объёма 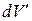 ), а
), а 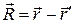 .
.
Аналогично, для вектор-потенциала 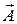
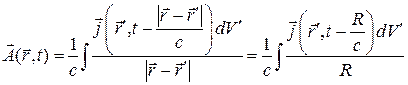 (21)
(21)
Наряду с этими решениями в виде запаздывающих потенциалов можно записать аналогичные в виде опережающих потенциалов.
