Нақта сандыр. Функция. Элементар функциялар.

Нәрселерді санау қажетінен тұған 1,2,3… натурал сандар ерте заманнан белгілі. Натурал сандар жиынын әдетте N әріпімен белгілейді.

Анықтама. Функция деп кез келген х элементіне, бірінші элементі осы х болатындай, біреуден артық емес (x,y) пары сәйкес келетін (x,y) парларының f жиынын атайды. Y=f(x). Парлардың бірінші элементтер (x) жиыны анықталу облысы деп, ал екінші элементтер жиыны (y) мәндер облысы деп аталады. Х аргумент деп аталады.

Анықтама. Егер кез келген х 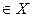мәніне сәйкес f(-x)= f(x) теңдігі орындалса, онда оны жұп функция деп атайды. Егер f(-x)= - f(x) болса, огда оны тақ функция деп атайды.

Мысалы, f(x)= 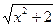. 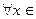R (кез келген х) үшін

f(-x)= 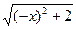= = 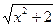f(x) орындалады. F функциясы жұп болады.

f(x)= 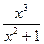. 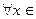R (кез келген х) үшін

f(-x)= 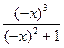= = 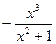-f(x) орындалады. F функциясы тақ болады.

Енді Y=f(x) функция үшін әр түрлі жағдайларды қарастырамыз.

1. f (x) орнегін алу үшін х аргументі мен тұрақты сандарға саны шектеулі алгебралық амалдар (қосу, алу, көбейту, бөлу, түбір табу) қолданылатын болса, онда өрнекті алгебралық өрнек деп атайды.

Мысалы у= 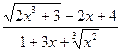формуласымен берілген функция алгебралық функция болады.

Алгебралық f(x) өрнегін құру үшін түбір табу амалы қолданылмаса, оны рационал өрнек деп атайды

Мысалы, у= 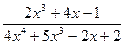рационал функция болады.

1. Тұрақты функция. Бұл функция f(x)=C формуламен береді. Бұл функциянын анықталу облысы бүкіл сандық өс (R жиыны), ал өзгеру облысы тек бір ғана тұрақты С санынан тұрады. Графиктері:

2. Дәрежелік функция. Бүтін қөрсеткіш функция деп f(x)=хⁿ функциясының атайды. Графиктері:

3. Көрсеткіш функция. Көрсеткіш функция деп у=a^x функциясын атайды. Анықталу облысы бүкіл сандық өс (R жиыны). Ал мәндер облысы нақты оң сандар жиыны болады. Графиктері:

4. Логарифмдік функция. Негізгі а (a 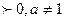) болатын логарифмдік функция деп көрсеткіш функцияға кері функцияны атайды және оны былай белгілейді y=log_ax Графиктері

5. Тригонометриялық функциялары. Y=cosx, y=sinx, y=tgx,y=ctgx. Графиктері

6. Кері тригонометриялық функциялары. y=arccosx, y=arcsinx, y=arctgx, y=arcctgx. Графиктері

Анықтама. Нақты санның модулі мына формуламен енгізіледі

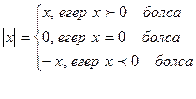
1-Анықтама. Тізбек деп барлық оң бүтін сандар жиынында анықталған f функциясын айтады. f функциясының оң бүтін санына сәйкес мәнін 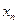деп белгілейді, яғни .

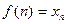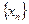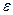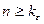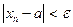2-Анықтама. тізбегі берілсін. Егер кез келген оң саны арқылы барлық үшін теңсіздігін қанағаттандыратын 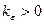саны табылса, онда 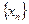тізбегінің нақты мәнді шегі бар және ол а санына тең деп атап, оны былай белгілейді: 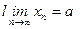немесе 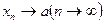(1)

Осы жағдайда 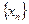тізбегін «а санына жинақталатын тізбек», «а санына ұмтылатын тізбек» деп те атайды.

Енді тізбектің қасиеттерін қарастырамыз.

1-Теорема. Жинақталатын тізбектің тек бір ғана шегі бола алады, яғни 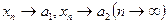болса, онда .

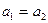2-Теорема. Егер 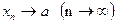болса, онда әрбір оң бүтін m үшін .

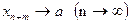3-Теорема. 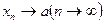болса, онда .

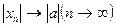4-Теорема. Шегі нөл емес нақты сан болатын тізбектің мүшелері белгілі бір нөмірден бастап шегінің таңбасын сақтайды.

5-Теорема. 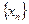және 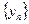тізбектерінің шектері бар болсын. Егер белгілі бір к нөмірінен бастап барлық n-дер үшін 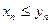теңсіздігі орындалса, онда сол теңсіздік шектер үшін де сақталады, яғни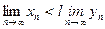

6-Теорема. 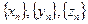тізбектері үшін келесі шарттар орындалса; 1) әрбір оң бүтін n үшін, 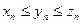; 2) 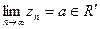; Онда 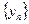тізбегінің де шегі бар және а-ға тең.