Параллельность прямой и плоскости

Прямая и плоскость параллельны, если в плоскости имеется пря­мая, параллельная заданной прямой.

7.3.1 Задание:построить проекции прямой, проходящей через точку А и параллельной прямой т, принадлежащей плоскости (BCD)(рис. 7.5).

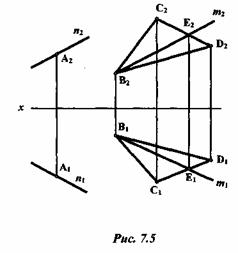
Решение:в условии задачи задана фронтальная проекция m₂ пря­мой m. Поэтому необходимо вначале найти горизонтальную проек­цию m₁ прямой m. Условия параллельности прямой и плоскости: пря­мая параллельна плоскости, если она параллельна какой-то прямой, расположенной в данной плоскости.

Используя это условие, строят проекции искомой прямой, прохо­дящие через точку А; п₁ проводится параллельно т₁, n₂ — параллель­но m_2.

ПРЯМАЯ ЛИНИЯ, ПЕРПЕНДИКУЛЯРНАЯ К ПЛОСКОСТИ

Основные положения

Обратимся к рисунку 8.1, на котором изображена плоскость и перпендикулярная к ней прямая п.

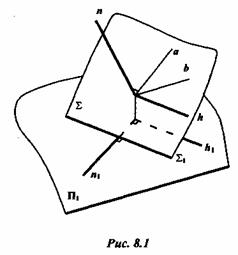
Прямая и перпендикулярна к любой прямой плоскости 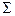, т.е. 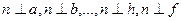. Каждый такой прямой угол проецируется на плоскость проекций в виде некоторого угла, но угол между прямой n и горизонталью плоскости h проецируется на горизонтальную плос­кость проекций прямым углом, так как его сторона h||П₁.

Если , то .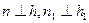

Угол между прямой п и фронталью 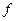плоскости проецируется на фронтальную плоскость проекций прямым углом (его сторона 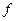|| П₂).

Если , то .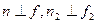

Если прямая перпендикулярна к плоскости, то ее проекции пер­пендикулярны к одноименным проекциям линий уровня этой плоско­сти.

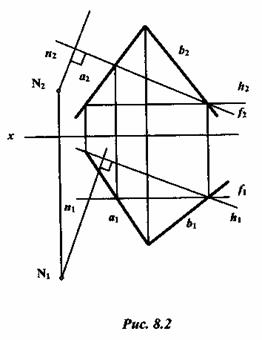
На рисунке 8.2 через точку N проведена прямая и, перпендику­лярная к плоскости 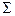. Для этого в плоскости 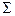(аxb) определены го­ризонталь h и фронталь 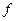, и горизонтальная проекция перпендикуляра проведена перпендикулярно к горизонтальной проекции горизонтали, а фронтальная проекция — перпендикулярно к фронтальной проек­ции фронтали: .

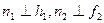В том случае, когда плоскость задана следами (рис. 8.3), проекции перпендикуляра располагаются перпендикулярно к одноименным следам плоскости: .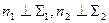

Рисунок 8.2 позволяет утверждать, что изображенные на нем пря­мая и и плоскость S взаимно перпендикулярны. Действительно, из чертежа следует, что прямая n перпендикулярна к прямой h, так как угол между горизонтальными проекциями сторон угла прямой и одна сторона его (h) параллельна плоскости П₁. Точно так же прямая и перпендикулярна к прямой 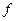. Но если прямая линия перпендикулярна к двум пересекающимся прямым плоскости, то она перпендикулярна к этой плоскости.

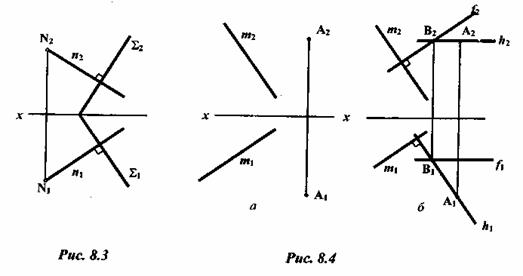
Плоскость, перпендикулярную к данной прямой, определяют с помощью пересекающихся линий уровня. На рисунке 8.4 (а - условие, 6 - решение) через данную точку А проведена плоскость 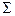, перпенди­кулярная к заданной прямой п. Горизонталь h плоскости проходит че­рез точку А ( 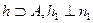). Фронталь этой плоскости может быть также проведена через точку А, но может пересекать горизонталь и в любой другой точке, поскольку все они находятся в искомой плоско­сти. На рисунке 8.4 фронталь f₂ проходит через точку В .

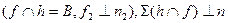На рисунке 8.5 показана прямая, перпендикулярная к горизон­тально проецирующей плоскости. Очевидно, эта линия является гори­зонталью.

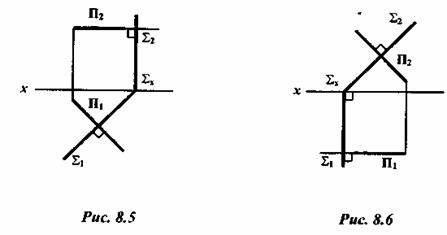
На рисунке 8.6 изображена прямая, перпендикулярная к фрон­тально проецирующей плоскости. Она является фронталью.

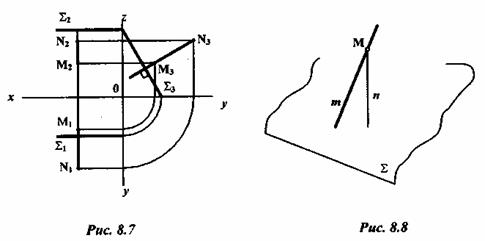
На рисунке 8.7 изображена прямая п (MN), перпендикулярная к профильно проецирующей плоскости 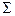. Заметим, что, проведя проек­ци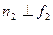и и 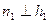мы еще не определим величину искомого пер­пендикуляра.

Это не должно нас удивлять, так как 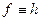, а перпендикулярность прямой и плоскости обеспечивается перпендикулярностью этой пря­мой к двум пересекающимся прямым плоскости. Для решения задачи нужно построить профильный след. Тогда .

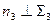Если требуется определить, перпендикулярна ли некоторая пря­мая т к заданной плоскости 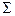, то через какую-нибудь точку М этой прямой следует провести перпендикуляр n к плоскости 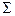(рис. 8.8).

При совпадении линии m и n прямая m перпендикулярна к плоскости .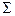

Примеры решения задач

8.2.1 Задание:опустить перпендикуляр из точки А на плоско­сть 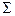( 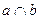) и найти его основание точку В.

Решение:исходя из принципа перпендикулярности прямой и плоскости (прямая перпендикулярна к плоскости, если она перпенди­кулярна к двум пересекающимся прямым этой плоскости), необходи­мо в плоскости провести две пересекающиеся прямые, а именно гори­зонталь h и фронталь 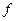(рис. 8.9).

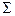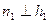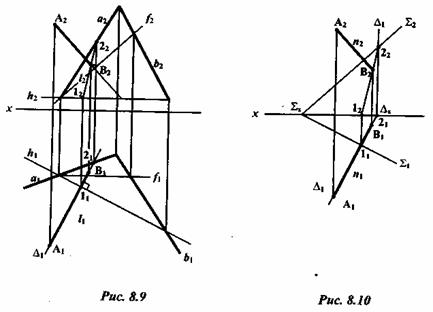
Затем из точки А проводим нормаль n к плоскости . На основа­нии теоремы о проецировании прямого угла и 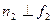. Если плоскость задана следами, то 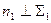и 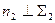(рис. 8.10). Основание перпендикуляра определяется как точка пересечения его с плоско­стью. Для этого нужно провести через нормаль проецирующую плос­кость 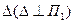, найти линию пересечения l(l₁,l₂)плоскосте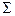й и 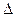и на пересечении этой линии и нормали отметить общую точку В для нормали и плоскости ( ).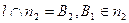