Понятие о пограничном слое. Уравнения ламинарного пограничного слоя в ньютоновской жидкости
Качественные теоретические соображения и опыт показывают, что в некоторых важных случаях вязкость жидкости проявляется главным образом только вблизи твёрдых стенок. Возникла теория пограничного слоя – тонкого слоя, внутри которого нельзя пренебрегать вязкостью [1], [6].
Мы рассматривали движение жидкости при малых числах Рейнольдса, методы пограничного слоя относятся к случаям движения при весьма больших числах Рейнольдса. В методе Стокса (Re<<1) инерционные члены совсем не учитывались, в методе Осеена эти члены учитывались лишь частично, в теории пограничного слоя инерционные члены учитываются полностью. В приближённых методах Стокса и Осеена вязкие члены учитываются полностью, в теории пограничного слоя эти члены учитываются лишь частично.
В теории пограничного слоя ньютоновских жидкостей принимают, что имеется основной поток жидкости, которую рассматривают как идеальную, и имеется тонкий пограничный слой, внутри которого жидкость рассматривается как вязкая; на границе пограничного слоя эти два течения сопрягаются.
Уравнения и основные понятия теории пограничного слоя были установлены в 1904 г. Л. Прандтлем.
В пограничном слое, так же как и при течении в трубе, режимы движения жидкостей или газов могут быть как ламинарными, так и турбулентными. При разных режимах течения основные характеристики движения жидкости и законы, управляющие ламинарным или осреднённым турбулентным движением в пограничном слое, получаются резко отличающимися друг от друга. Ниже мы рассмотрим теорию ламинарного пограничного слоя.
Для получения уравнения теории пограничного слоя рассмотрим основную модельную задачу об обтекании несжимаемой ньютоновской жидкостью неподвижной тонкой пластинки, поставленной по скорости набегающего поступательного потока перед пластинкой [1].
Вывод уравнения движения в пограничном слое основан на оценках-гипотезах о порядке различных членов в уравнениях Навье – Стокса и пренебрежении малыми членами; сохраняются только конечные члены.
Для плоскопараллельного движения в плоскости xy имеем следующие уравнения движения вязкой несжимаемой жидкости:
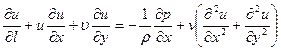 (5.1)
(5.1)
1 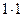
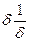 1
1 
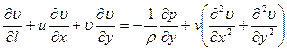 (5.2)
(5.2)
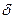
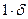

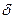

 (5.3)
(5.3)
1 1
Пусть l – некоторый характерный размер, например размер пластинки. Обозначим через 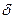 «толщину» пограничного слоя. По основному допущению примем, что на расстоянии
«толщину» пограничного слоя. По основному допущению примем, что на расстоянии 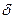 по нормали от обтекаемой поверхности (пластинки) имеется «граница» пограничного слоя, на которой скорости жидкости извне и изнутри пограничного слоя практически совпадают (практическая малость разности скоростей в процентном или в некотором другом отношении определяется дополнительным условием).
по нормали от обтекаемой поверхности (пластинки) имеется «граница» пограничного слоя, на которой скорости жидкости извне и изнутри пограничного слоя практически совпадают (практическая малость разности скоростей в процентном или в некотором другом отношении определяется дополнительным условием).
Величина 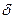 или отношение
или отношение 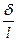 принимается в качестве основной малой величины. Воспользуемся преобразованием:
принимается в качестве основной малой величины. Воспользуемся преобразованием:
 ,
, 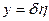 (5.4)
(5.4)
и предположим, что в пограничном слое переменные  ,
,  и
и  изменяются в конечных пределах, а интервал изменения переменной
изменяются в конечных пределах, а интервал изменения переменной  имеет порядок
имеет порядок 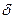 . Дальше примем, что велечины
. Дальше примем, что велечины  ,
, 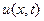 , их производные по времени и производные
, их производные по времени и производные  внутри пограничного слоя и на его границе с основным потоком конечны.
внутри пограничного слоя и на его границе с основным потоком конечны.

Рис. 5.1
Из равенств
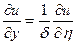 ,
,  ,
,
так как 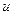 и
и  изменяются в конечных пределах, следует, что
изменяются в конечных пределах, следует, что

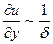 ,
,  . (5.5)
. (5.5)
Далее, из уравнения неразрывности имеем
 ,
,  ,
,  ,
,  ,
,  . (5.6)
. (5.6)
На основании этих оценок под каждым членом уравнений (5.2) и (5.3) указан порядок его величины.
Уравнение (5.1) показывает, что при конечных l и U должно быть конечным  , в безразмерном виде должно быть
, в безразмерном виде должно быть
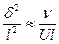 или
или  (5.7)
(5.7)
Эти прикидочные оценки и послужили основой для упрощения уравнений Навье-Стокса в пограничном слое. После сохранения в (5.1), (5.2) только конечных членов получаются следующие уравнения пограничного слоя:
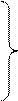
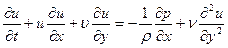 , (5.8)
, (5.8)
 или
или  .
.
К этим уравнениям необходимо добавить уравнение неразрывности (5.3). Уравнения (5.8) остаются линейными. Поперёк пограничного слоя давление сохраняется постоянным и определяется значением на границе слоя в основном потоке, рассчитываемым из теории идеальной жидкости, следовательно, в уравнении (5.8) член 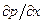 можно считать известным.
можно считать известным.
В отличие от уравнений Навье-Стокса система уравнений (5.8) и (5.3) поддаётся решению в ряде важных случаев. При приближённых расчётах эта система применяется не только для исследования движения в пограничном слое на плоской пластинке, но и для исследования движения в пограничном слое на криволинейных профилях. В общем случае принимается, что координата x представляет собой длину дуги вдоль профиля, а координата y измеряется по нормали к профилю. Зависимость U(x,t), задающая скорость на внешней границе пограничного слоя, определяется из решения соответствующей задачи теории идеальной жидкости. Предложены уточнения уравнений (5.8) для учёта криволинейности обтекаемых профилей и для исследования пространственных задач.
Более формальный математический вывод уравнений (5.8) с более определённой формулировкой соответствующих предположений можно дать следующим образом. В уравнениях (5.1) и (5.2) сделаем следующее преобразование переменных:

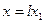 ,
,  , (5.9)
, (5.9)
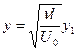
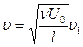 ,
, 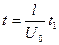 ,
,  ,
,
где 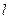 и
и 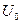 - некоторые постоянные - характерные линейный размер и скорость. Выполнив это преобразование, получим
- некоторые постоянные - характерные линейный размер и скорость. Выполнив это преобразование, получим

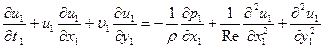 ,
,
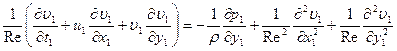 , (5.10)
, (5.10)
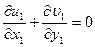 ,
,
где 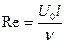 - число Рейнольдса. Эти уравнения представляют собой точные уравнения Навье-Стокса, записанные в соответствующих безразмерных переменных.
- число Рейнольдса. Эти уравнения представляют собой точные уравнения Навье-Стокса, записанные в соответствующих безразмерных переменных.
Предположим теперь, что при 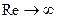 все величины с индексом 1 в (5.9) и (5.10) сохраняют конечные значения. После перехода к пределу при
все величины с индексом 1 в (5.9) и (5.10) сохраняют конечные значения. После перехода к пределу при 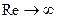 из (5.10) получим:
из (5.10) получим:

 ,
,
 , (5.11)
, (5.11)
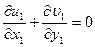 .
.
Эти уравнения после обратного преобразования с помощью (5.9) переходят в уравнения (5.8) и (5.3). Таким образом, уравнения пограничного слоя можно рассматривать в некотором смысле как предельную форму уравнений Навье-Стокса, когда число Рейнольдса  стремится к бесконечности.
стремится к бесконечности.
В задачах об обтекании профилей необходимо решать систему (5.11) со следующими граничными условиями:  ,
, 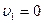 при
при 
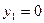 (условие прилипания на профиле) и
(условие прилипания на профиле) и  при
при  (условие на внешней границе пограничного слоя), причём внутри пограничного слоя
(условие на внешней границе пограничного слоя), причём внутри пограничного слоя 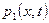 не зависит от
не зависит от 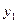 и определяется из решения задачи о внешнем обтекании.
и определяется из решения задачи о внешнем обтекании.
Задача о внешнем обтекании профиля идеальной жидкостью в первом приближении может быть решена без учёта наличия пограничного слоя, так как для толщины пограничного слоя по (5.7) имеем
 при
при 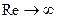 ,
,
т.е. толщина пограничного слоя получается очень малой при больших значениях числа Рейнольдса, характерных для многих практически важных задач.
