Конденсаторы и их соединения
Конденсатор –это устройство,которое способно при неболь-шом относительно окружающих тел потенциале накапливать суще-ственный заряд. Если два проводника имеют такую форму, что соз-даваемое ими электрическое поле сосредоточено в ограниченной области пространства, то образованная ими система носит название
конденсатора,а сами проводники называют обкладками конденса-
тора.В этом случае линии электрического смещения начинаютсяна одной обкладке и заканчиваются на другой. Электрические заря-ды, находящиеся на обкладках заряженного конденсатора, всегда равны по величине и противоположны по знаку. Таким образом, конденсатор представляет собой систему двух проводников,изоли-рованных друг от друга. Кроме того, один из проводников должен быть изолирован от земли.
В зависимости от формы обкладок различают плоские, сфериче-ские и цилиндрические конденсаторы.Основной характеристикой кон-денсатора является электрическая емкость, под которой понимают физическую величину, пропорциональную заряду и обратно пропор-циональную разности потенциалов между обкладками:
| C | q | q | , | (4.2.1) | ||||
| U | ||||||||
где q – заряд одной из обкладок; 1 – 2 = U – разность потенциалов (напряжение) между обкладками.
Величина емкости определяется геометрией конденсатора (фор-мой и размерами обкладок и величиной зазора между ними), а также диэлектрической проницаемостью среды, заполняющей пространст-во между обкладками. В случае если между обкладками конденсатора
находится сегнетоэлектрик, диэлектрическая проницаемость которо-го зависит от напряженности поля, то пропорциональность между q и
нарушается, а конденсаторы называются нелинейными.
Получим формулы для расчета емкости различных типов конден-саторов.
Плоский конденсатор (рис. 4.2.1)состоит из двух параллельныхметаллических пластин (площадь каждой S), расположенных на близ-ком расстоянии d одна от другой и несущих заряды q1 > 0 и q 2 < 0 (|q1| = |q2|). Пространство заполнено средой, диэлектрическая проницае-
мость которой . Зазор d между пластинами мал по сравнению с их размерами, т. е. краевым эффектом можно пренебречь.
+q2
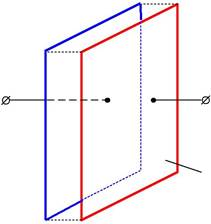
–q1
| S | ||||||||||||
| d | Рис. 4.2.1 | |||||||||||
| Напряженность поля между обкладками E | . Так как | q | , | |||||||||
| 0 | S | |||||||||||
| q | ||||||||||||
| то E | . | |||||||||||
| 0 | 0S | |||||||||||

| d | Edr | q | d | dr | qd | |||||
| Тогда | . Учитывая формулу (4.2.1), | |||||||||
| S | S | |||||||||
получим формулу для расчета емкости плоского конденсатора:
| C | 0S . | (4.2.2) |
| d |
Сферический конденсатор (4.2.2)состоит из двух концентриче-ских металлических сферических обкладок, радиусы которых R1 и R2 (R2 > R1), а пространство между обкладками заполнено диэлектриком
с диэлектрической проницаемостью . Заряды обкладок обозначим через +q и – q, а потенциалы обкладок – соответственно 1 и 2 и бу-дем считать заряд равномерно распределенным по поверхности. Ис-пользуя теорему Гаусса, легко показать, что электрическое поле суще-ствует только в пространстве между сферами, и напряженность этого
поля E 1 q2 . Напряженность поля связана с разностью потен-4 0 r
| циалов соотношением d Edr | q | dr. | |||
| 4 0 | r2 | ||||
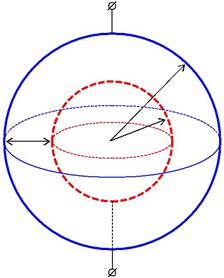
R2
| d | R1 | |
+q
–q
Рис. 4.2.2
Полное изменение потенциала при переходе с одной обкладки на другую получим интегрированием от R1 до R2:
| q | R2 | dr | q | q | R1 R2 | . | |||||||||||||||
| r2 | R | R | |||||||||||||||||||
| R R | |||||||||||||||||||||
| R | 1 2 | ||||||||||||||||||||
Подставив выражение для разности потенциалов в (4.2.1), полу-чим формулу для расчета емкости сферического конденсатора:
| C | 40 R1 R2 . | (4.2.3) |
| R2 R1 |
Если R2 – R1 = d << R1 , то можно считать R2 R1 . Тогда
| C | 4R2 | 4 R 2 | S | , | ||||||
| 0 1 | ||||||||||
| d | d | d |
где S 4 R12 – площадь поверхности обкладок.
Таким образом, если величина зазора между обкладками сфериче-ского конденсатора мала по сравнению со средним радиусом сфер, то емкость сферического конденсатора можно приближенно рассчитать по формуле для емкости плоского конденсатора.
Цилиндрический конденсатор (рис. 4.2.3)представляет собой двакоаксиальных (т. е. имеющих одну ось симметрии) полых цилиндра с радиусами R1 и R2 (R2 > R1) и общей длиной l.
| –q | |||
| d | +q | R2 | |
| R1 | |||
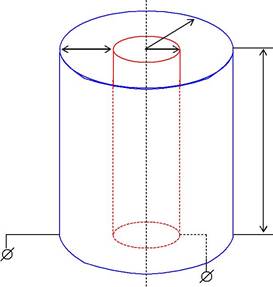
l
Рис. 4.2.3
Пусть на обкладках имеются заряды +q и –q, потенциалы которых соответственно 1 и 2, а пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Пренебрегая краевыми эффектами на торцах цилиндров, напряженность поля, соз-даваемая только зарядом на внутреннем цилиндре в точке на расстоя-
| нии r от оси цилиндра, можно найти по формуле E | . Тогда | ||||||||||||||||||
| 2 0 | r | ||||||||||||||||||
| dEdr | dr .Разность | потенциалов | между обкладками | ||||||||||||||||
| 2 0 | r | ||||||||||||||||||
| получим интегрированием от R1 до R2: | |||||||||||||||||||
| R2 | dr | R | |||||||||||||||||
| ln | . | ||||||||||||||||||
| 2 0 | r | 2 0 R1 | |||||||||||||||||
| R | |||||||||||||||||||
Подставив выражение для разности потенциалов в (4.2.1), полу-чим формулу для расчета емкости цилиндрического конденсатора:
| C | 2 0l | . | (4.2.4) | |||||
| ln R | R | |||||||
| Если зазор (d = R2 – R1) между обкладками мал по сравнению с R1, | ||||||||
| то ln(R2/R1) (R2 – R1)/R1 и | ||||||||
| C | 2 0lR1 | 0S | , | |||||
| R | R | d | ||||||
 где S = 2 R1l – площадь обкладки.
где S = 2 R1l – площадь обкладки.
Помимо емкости каждый конденсатор характеризуется предель-ным напряжением, которое можно прикладывать к обкладкам конден-сатора, не опасаясь пробоя. При превышении этого напряжения между обкладками проскакивает искра, в результате чего разрушается диэлек-трик, и конденсатор выходит из строя. Величина пробивного напряже-ния зависит от свойств диэлектрика, его толщины и формы обкладок.
Для того чтобы получить желаемую емкость при заданном рабо-чем напряжении, конденсаторы соединяют в батареи (параллельно или последовательно).
Рассмотрим параллельное соединение конденсаторов (рис. 4.2.4). При таком соединении разность потенциалов на обкладках конденса-торов одинакова. Заряды соответственно равны: q1 = C1( 1 – 2); q2 = = C2( 1 – 2); …; qn = Cn( 1 – 2). Тогда заряд батареи конденсаторов
n
q qi C1 C2... Cn 1 2,а полная емкость батареи опре-
i 1
деляется следующим образом:
| q | C C | C | ||||||||
| C | n | C1 C 2Cn , | ||||||||
или
| n | |
| CCi , | (4.2.5) |
i 1
т. е. при параллельном соединении конденсаторов полная емкость равна сумме емкостей отдельных конденсаторов.

U =1–2  |
| +q1 | +q2 1 | |||||
| –q1 | C1 | C2 | ||||
| –q2 2 | ||||||
| Рис. 4.2.4 |

…
…
+qn 1
 Cn
Cn

–qn 2
Рассмотрим последовательное соединение конденсаторов (рис. 4.2.5). При таком соединении заряды всех обкладок равны по модулю. Если одной обкладке первого конденсатора сообщить заряд +q , то на его второй обкладке индуцируется заряд –q, а на соединенной с ней пер-вой обкладке второго конденсатора появится заряд +q и т. д. Разность
n
потенциалов на зажимах батареи i , где для любого
i 1
конденсатора i q .
Ci
| +qC1 –q | +q C2 –q … | +q Cn –q | ||||||||||||||||||
| n–1 | n | |||||||||||||||||||
| U1 | U2 | Un | ||||||||||||||||||
| U =1–2 | ||||||||||||||||||||
| Рис. 4.2.5 | ||||||||||||||||||||
| q | n | |||||||||||||||||||
| Тогда | q | , откуда полная емкость | ||||||||||||||||||
| C | Ci | |||||||||||||||||||
| i 1 | ||||||||||||||||||||
| n | ||||||||||||||||||||
| , | (4.2.6) | |||||||||||||||||||
| C | Ci | |||||||||||||||||||
| i 1 |
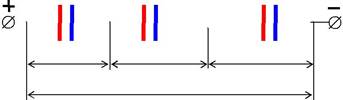
т. е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям.
Таким образом, при последовательном соединении конденсаторов результирующая емкость всегда меньше наименьшей емкости, ис-пользуемой в батарее.
При смешанном соединении конденсаторов емкость батареи кон-денсаторов можно рассчитать, используя формулы (4.2.5) и (4.2.6).
