Обнаружение и исключение ошибок

Надежность эргономической системы, в которую входят человек, окружающая среда, объект измерений и средство измерений не безгранична. В ней могут происходить сбои, отказы аппаратуры, скачки напряжения в сети питания, сейсмические сотрясения, отвлечение внимания оператора, описки в записях и многое другое, не имеющее отношения к измерениям. В результате появляются ошибки, вероятность которых, как следует из теории надежности больших систем, не так уж мала.

При однократном измерении ошибка может быть обнаружена только путем логического анализа или сопоставления результата с априорным представлением о нем. Установив и устранив причину ошибки, измерение можно повторить.

При многократном измерении одной и той же величины постоянного размера ошибки проявляются в том, что результаты отдельных измерений заметно отличаются от остальных. Иногда это отличие настолько большое, что ошибка очевидна. Остается понять и устранить ее причину или просто отбросить этот результат как заведомо неверный. Если отличие незначительное, то оно может быть следствием, как ошибки, так и рассеяния отсчета, а, следовательно, показания результата измерения, которые согласно основному постулату метрологии являются случайными. Необходимо поэтому иметь определенное правило, руководствуясь которым, можно было бы принимать решения в сомнительных случаях.

После того, как все влияющие факторы учтены, и все поправки в показания внесены, рассеяние результата измерения одной и той же физической величины постоянного размера нередко бывает следствием множества причин, вклад каждой из которых незначителен по сравнению с суммарным действием всех остальных. Центральная предельная теорема теории вероятности утверждает, что результат измерения при этом подчиняется так называемому нормальному закону.Интегральная функция нормального закона распределения.

.

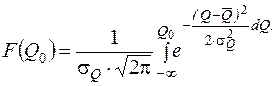Если условия центральной предельной теоремы выполняются, то весь массив экспериментальных данных при многократном измерении одной и той же величины постоянного размера должен группироваться около среднего значения 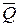, и выпадение какого-нибудь отдельного значения результата измерения из этого массива позволяет предположить, что он ошибочный. Найдем вероятность, с которой любое значение результата измерения, подчиняющегося нормальному закону распределения вероятности, должно находиться в пределах от Q₁ до Q₂:

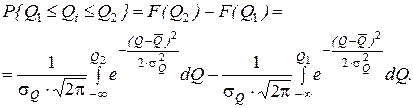
где Q₁; Q₂ равноотстоящие от среднего значения Q на ± t σ_Q, то есть

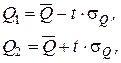
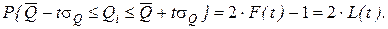
L(t) – функция Лапласа.

Параметр t играет в метрологии важную роль. Он показывает, насколько σ_Q с заданной вероятностью может отличаться отдельное значение результата измерения, подчиняющегося нормальному закону распределения вероятности, от своего среднего значения.

Эта вероятность называется доверительной, интервал 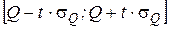– доверительным интервалом, а его границы Q₁ и Q₂ – доверительными границами. Из графика следует, что доверительный интервал зависит от доверительной вероятности. С очень высокой вероятностью 0,997 все значения результата измерения, подчиняющегося нормальному закону, должны группироваться в пределах доверительного интервала 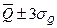. На этом основании можно сформулировать следующее правило: если при многократном измерении одной и той же физической величины постоянного размера сомнительное значение результата измерения отличается от среднего значения больше чем на 3 σ_Q, то с вероятностью 0,997 оно является ошибочным и его следует отбросить. Это правило называется «правилом трех сигм» или критерием .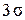