Последовательный контроль

. Последовательный контроль можно рассматривать как придельный случай многоступенчатого контроля. При этом методе объём выборки не фиксируется – отдельные единицы извлекают из партии случайным образом и проверяют. После каждой проверки принимают одно из трёх решений: принять партию, продолжить проверку, забраковать партию.

Такой метод контроля иногда по имени автора – методом Вальда. Метод основан на том, что для каждой i-й последовательной независимой проверки можно вычислить отношения правдоподобия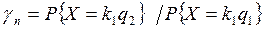

т.е. отношение вероятности получить ровно k дефектных единиц продукции и выборки из партии с уровнем дефектности 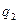к вероятности получить то же количество дефектных единиц продукции в выборке из партии с уровнем дефектности 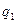В формулу подставляется значение вероятности 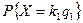согласно биномиальному распределению или распределению Пуассона.

Вальд доказал, что можно обеспечить заданные риски поставщика и потребителя 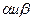, применяя следующее решающее правило:

-если выполняется неравенство

,

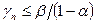то партию следует принять;

-если окажется, что

,

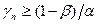то партию следует браковать;

-при

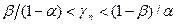
проверку следует продолжать.

На практике нет необходимости вычислять это отношение после проверки каждой единицы продукции. Логарифмируя неравенства можно получить уравнения прямых, по которым вычисляют и наносят на график линии k1 и k2 (рис. 3.11).

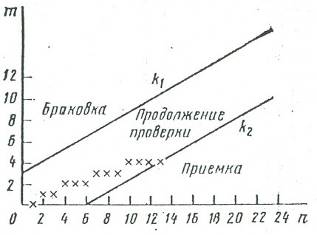
Рис. 3.11

По горизонтальной оси графика откладывают накопленное число проверенных единиц продукции n. По вертикали – накопленное число дефективных единиц продукции m. График с двумя прямыми k1 и k2 заготовляют заранее и в ходе приёмного контроля на него наносят опытные точки (n, m), отмеченные на рисунке крестиками. Как только траектория этих точек выйдет из зоны продолжения проверок, принимают решение о приёмке или браковке партии.

Найдём уравнения прямых на графике (Рис. 3.11) при биномиальном распределении числа дефектных единиц продукции в выборке. Подставив в выражение для соответствующих вероятностей, получим уравнение линии забраковки

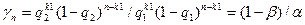
Откуда прологарифмировав, получим

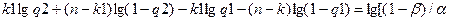
После преобразований имеем

;

,

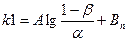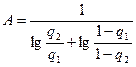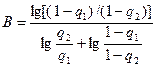
По аналогии получим уравнение линии приёмки

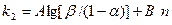
Обе линии на графике параллельны.

Метод последовательного контроля позволяет значительно сократить среднее число проверяемых единиц продукции по сравнению с одно- и двухступенчатым контролем при одинаковых операционных характеристиках. Однако при этом методе трудно планировать проверки, так как неизвестно заранее количество проверяемых единиц продукции. Поэтому иногда применяют усечённый последовательный контроль, при котором испытания ведутся сначала по методу последовательного контроля. Если они не закончились при 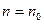, то результаты оцениваются как при одноступенчатом контроле.

Процедура последовательных проверок может применяться не только для отдельных единиц продукции, но и для выборок.