Проверка на случайность ряда остатков

Для проверки случайности остаточной компоненты ε можно использовать критерий поворотных точек (пиков).

Опр. Точки считаются поворотными, если:

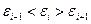или .

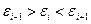Пусть число поворотных точек равно р, тогда если

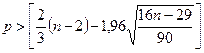[2],

то гипотеза о случайности остаточной компоненты ε с доверительной вероятностью 0,95 выполняется.

Проверка на равенство нулю математического ожидания ряда остатков

Среднее значение ряда остатков рассчитывается по формуле:

.

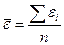Если 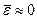, то модель не содержит постоянной систематической ошибки и адекватна по критерию нулевого среднего.

Если 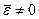, то для проверки гипотезы о M[ε] = 0 используем t ‑ критерия Стьюдента.

Расчетное значение этого критерия задается формулой:

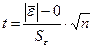
Если 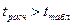то модель гипотеза о том M[ε] = 0 не выполняется.

Проверка на постоянство дисперсии ряда остатков

Если D[ε] ≠ 0, то используют метод Гольдфельда-Квандта:

- необходимо ранжировать переменную x_i;

- разделить полученную совокупность на две части;

- по каждой группе построить уравнение регрессии;

- определить остаточные суммы квадратов по формулам:

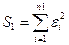и ,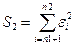

где n1 – число наблюдений в первой группе;

n2 – число наблюдений во второй группе.

- если S₁> S₂ критерий ;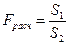

- если S₂> S₁ критерий .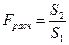

- чем F_расч > F_табл, тем больше нарушена предпосылка о постоянстве дисперсий остаточных величин.

Проверка на независимость ряда остатков

Независимости уровней ряда остатков проверяем по критерию Дарбина-Уотсона.

Вычислить значение:

.

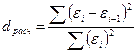d_расч сравнивают с нижним d₁ и верхним d₂, по таблице.

Если d_расч> d₁, то гипотеза о независимости ряда остатков выполняется.

Если d₁ <d_расч< d₁, то используют первым коэффициентом автокорреляции:

.

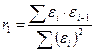И если r₁ по модулю меньше табличного критического уровня r_крит, то гипотеза о независимости ряда остатков выполняется.

Если d₂ < d_расч < 2, то гипотеза о независимости ряда остатков выполняется.

Если d_расч > 2, то модель остатки коррелируют отрицательно,

Необходимо принять за d^/ = 4 – d.

Проверка на распределение ряда остатков по нормальному закону

Используем R/S – критерий.

В нашем случае

.

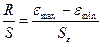Расчетное значение R/S_ε сравнивают с табличными значениями (нижней и верхней границами данного отношения), и если значение не попадает в интервал между критическими границами, то с заданным уровнем значимости гипотеза о нормальном распределении отвергается; в противном случае гипотеза принимается.

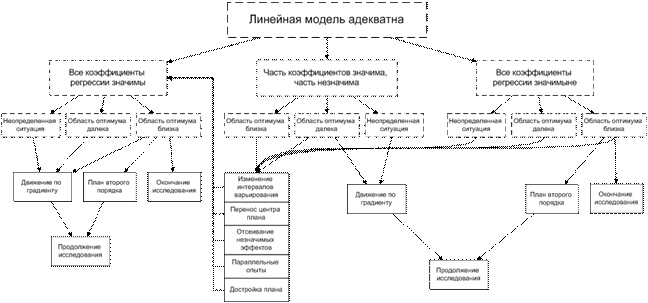
Если ВСЕ вышеперечисленные критерии дают положительный ответ, модель АДЕКВАТНА.