Методи багатовимірної оптимізації
ЛЕКЦІЯ № 5
В літературі можна знайти роздуми відносно того, що задачу багатовимірного пошуку екстремуму функції з n аргументами можна розв’язувати як певну сукупність задач одновимірного пошуку і що це призводить тільки до збільшення обсягу обчислень, яке в n разів більше, ніж при одновимірній оптимізації. Але в дійсності це не так, оскільки багатовимірний простір якісно відрізняється від одновимірного. Перш за все зі збільшенням розмірності просторе зменшується ймовірність унімодальності цільової функції. Крім того, множина елементів, що утворюють багатовимірний простір, значно потужніше множини елементів одновимірного простору. Обсяг обчислень, необхідних для звуження інтервалу невизначеності в багатовимірному просторі, є степеневою функцією, показник якої дорівнює розмірності простору. Так, якщо в одновимірному просторі для отримання прийнятної точності треба розрахувати 19 значень цільової функції, то у випадку двовимірного простору кількість розрахунків становитиме 361, тривимірного простору – 6859, чотирьохвимірного – 130321 і, нарешті, п’ятивимірного – 2476099. Наведені числові дані вказують на серйозні обчислювальні труднощі при розв’язанні оптимізаційних задач в багатовимірному просторі параметрів.
Традиційно методи оптимізації в багатовимірному просторі діляться на дві великі групи – прямі і непрямі. Прямі методи засновані на порівнянні обчислених значень цільової функції в різних точках, а непрямі – на застосуванні необхідних і достатніх умов математичного визначення максимуму чи мінімуму функції. Стратегія прямих методів – поступове наближення до оптимуму; при використанні непрямих методів прагнуть знайти рішення, не досліджуючи неоптимальні точки.
Розрізняють також методи безумовної та умовної оптимізації. Розглянемо спочатку методи безумовної багатовимірної оптимізації.
5.1. Постановка задачі багатовимірної оптимізації
Незважаючи на різні постановки оптимізаційних задач їх структура майже однотипна і містить наступні компоненти.
1. Цільова функція 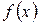 n-вимірного векторного аргументу
n-вимірного векторного аргументу 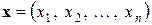 , тобто
, тобто
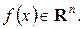
2. Обмеження у вигляді нерівностей 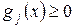 .
.
3. Обмеження у вигляді рівностей 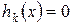 .
.
4. Область допустимих значень 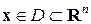 .
.
У загальному випадку задача багатовимірної оптимізації формулюється наступним чином:
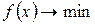
обмеження І роду 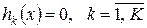 ,
,
обмеження ІІ роду 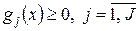 ,
,
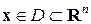
Задача багатовимірної безумовної оптимізації записується наступним чином
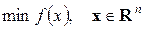
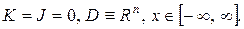
Тобто, обмеження або відсутні, або є пустими множинами.
Задача багатовимірної умовної оптимізації записується дещо інакше, оскільки є обмеження
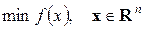
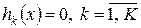
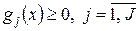
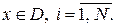
5.2. Необхідні і достатні умови мінімуму гладких функцій
кількох змінних
Методи багатовимірної безумовної оптимізації аналогічні методам одновимірної оптимізації і визначені необхідними і достатніми умовами екстремуму.
В табл. 5.1 наведено зіставлення умов існування екстремуму.
Таблиця 5.1.
Умови існування екстремуму
| Умови екстремуму | R1 | Rn |
| Необхідні | Стаціонарна точка 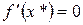 | Вектор-градієнт 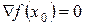 |
| Необхідні і достатні | 1. Стаціонарна точка 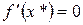 2. 2. 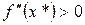 | 1. Вектор-градієнт 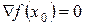 2. Матриця Гессе додатно визначена 2. Матриця Гессе додатно визначена |
Під градієнтом розуміють вектор, проекції якого на осі координат є частинними похідними.
Введемо вектор-градієнт
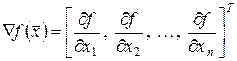
і дійсну матрицю Гесе (гесіан)
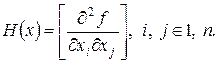
Наприклад, для 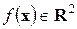
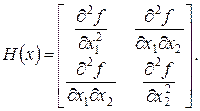
Матриця Гесе 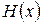 – симетрична.
– симетрична.
Теорема 1. Для того, щоб функція 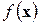 , яка диференціюється на множині
, яка диференціюється на множині 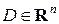 , мала в точці
, мала в точці 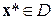 локальний екстремум необхідно, щоб
локальний екстремум необхідно, щоб 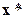 була стаціонарною точкою, тобто
була стаціонарною точкою, тобто
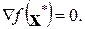
Теорема 2. Критерій Сильвестра.
Якщо 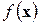 є функцією двічі диференційованою на
є функцією двічі диференційованою на 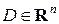 та її гесіан додатно визначений при всіх
та її гесіан додатно визначений при всіх 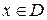 , то функція
, то функція 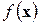 є опуклою на множині
є опуклою на множині 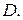
Критерії визначеності матриці 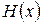
Додатна визначеність матриці означає:
– всі діагональні елементи додатні;
– визначники всіх головних мінорів матриці додатні.
Додатна напіввизначеність матриці означає:
– всі діагональні елементи матриці більше або дорівнюють нулю;
– визначники всіх головних мінорів більше або дорівнюють нулю.
Приклад. Оціните визначеність гесіана для функції
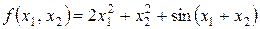 .
.
Знаходимо похідні першого і другого порядку
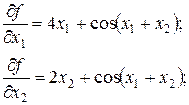
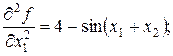
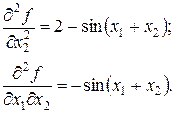
Запишемо матрицю Гесе
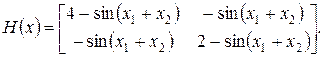
Головні мінори:
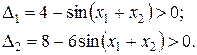
Отже, гесіан додатно визначений і функція 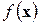 є опуклою.
є опуклою.
Теорема 3. Необхідні і достатні умови існування мінімуму багатовимірної функції 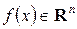 :
:
– існує стаціонарна точка, тобто вектор-градієнт 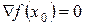 ;
;
– матриця Гесе додатно визначена.
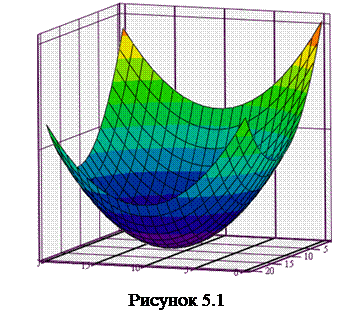
Методи пошуку екстремуму багатовимірної функції не мають наочної геометричної ілюстрації, як це має місце в одновимірному випадку. Наочність має місце тільки двовимірний випадок пошуку екстремуму функції. Розглянемо графічне розв’язання для наступного прикладу.
Приклад. Дано сепарабельну функцію, тобто функцію, в якій аргументи не впливають один на одного
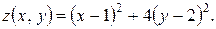
Наочне зображення функції наведено на рис. 5.1, а лінії рівня – на рис. 5.2.
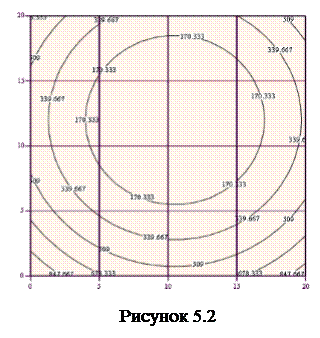
Треба знайти екстремум функції при початкових умовах 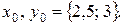
Зазначимо, що існує точне рішення
 |
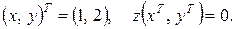
 |
5.3. Метод покоординатного спуску
Розглянемо алгоритм пошуку мінімуму багатовимірної функції методом покоординатного спуску на прикладі функції двох змінних 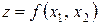 . Графік цієї функції в області її мінімуму представимо в параметричному вигляді, подібно зображенню рельєфу місцевості на географічних картах, з’єднуючи лініями точки на координатній площині
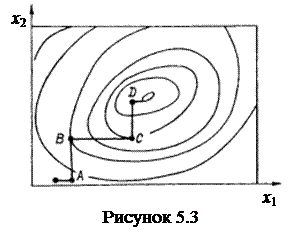
. Графік цієї функції в області її мінімуму представимо в параметричному вигляді, подібно зображенню рельєфу місцевості на географічних картах, з’єднуючи лініями точки на координатній площині 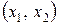 , де функція приймає однакові значення (рис. 5.3).
, де функція приймає однакові значення (рис. 5.3).
 |
Припустимо, що нам відома прямокутна область на площині
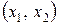 , де знаходиться мінімум функції
, де знаходиться мінімум функції 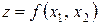 , тобто
, тобто 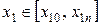 ,
, 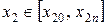 .
.
Алгоритм покоординатного пошуку полягає в зведенні багатовимірної задачі до послідовності одновимірних задач, які розв’язуються методами мінімізації функції однієї змінної, зокрема, методом золотого перерізу.
Процес оптимізації проходить наступним чином.
Фіксують змінну х2 в точці 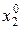 . Тоді
. Тоді 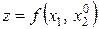 буде функцією однієї змінної х1. Розв’язують задачу одновимірної оптимізації по змінній х1 методом золотого перерізу. На рис. 5.3 знайдений мінімум розташовується в точці
буде функцією однієї змінної х1. Розв’язують задачу одновимірної оптимізації по змінній х1 методом золотого перерізу. На рис. 5.3 знайдений мінімум розташовується в точці 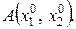 Далі фіксують перший аргумент
Далі фіксують перший аргумент 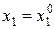 і знаходять мінімум
і знаходять мінімум 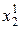 функції
функції 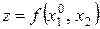 відносно другого аргументу х2 (точка
відносно другого аргументу х2 (точка 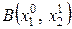 на рис. 5.3). Аналогічним чином послідовно переходять до точок
на рис. 5.3). Аналогічним чином послідовно переходять до точок 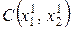 ,
, 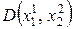 і т.д.
і т.д.
Якщо в області мінімуму функції функція 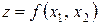 достатньо гладка, то процес спуску по координатах буде лінійно сходитися до мінімуму.
достатньо гладка, то процес спуску по координатах буде лінійно сходитися до мінімуму.
У процесі, що сходиться, з наближенням до мінімуму функції 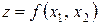 відстань між послідовними точками однокоординатних мінімумів буде прагнути до нуля. Тому в якості критеріїв завершення ітераційного процесу покоординатного спуску вибираються умови
відстань між послідовними точками однокоординатних мінімумів буде прагнути до нуля. Тому в якості критеріїв завершення ітераційного процесу покоординатного спуску вибираються умови
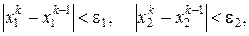
де ε1 і ε2 – задані допустимі абсолютні похибки визначення місцерозташування мінімуму по першій та другій координатам.
Метод покоординатного спуску легко узагальнюється на випадок функцій з розмірністю більше двох. Але треба мати на увазі, що з ростом розмірності значно збільшується обсяг обчислень.
Метод покоорднатного спуску часто застосовують на першій стадії розв’язання оптимізаційної задачі, продовжуючи її більш складними методами.
Зауваження.
1. Метод покоординатного спуску не застосовується у випадку наявності зломів в лініях рівня, тобто поверхонь з ярами і гребенями.
2. Перевагою методу є можливість застосування простих алгоритмів одновимірної оптимізації.
3. Метод застосовує тільки необхідні умови екстремуму. Це може призвести до локального екстремуму.
5.4. Метод градієнтного спуску
Відомо, що градієнт функції 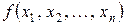 в кожній точці направлений в бік найшвидшого локального зростання цієї функції. Отже, для пошуку мінімуму необхідно спускатися в протилежному напрямку. Градієнт змінюється при переході з точки в точку, отже, змінюється і напрямок найшвидшого убування функції.
в кожній точці направлений в бік найшвидшого локального зростання цієї функції. Отже, для пошуку мінімуму необхідно спускатися в протилежному напрямку. Градієнт змінюється при переході з точки в точку, отже, змінюється і напрямок найшвидшого убування функції.
Якщо функція, яка мінімізується, є функцією диференційованою та обмеженою знизу, то ітераційний процес
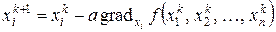 (5.1)
(5.1)
буде збігатися до мінімуму функції f із довільної початкової точки з координатами 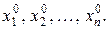
Параметр а в формулі (5.1) визначає довжину кроку в напрямку спуску і забезпечує виконання мети оптимізації.
Реалізація простішого алгоритму на основі формули пошуку (5.1) має назву методу градієнтного пошуку і включає два етапи.
1. Пробний крок для визначення напрямку градієнта.
2. Одночасне зміщення в бік градієнта всіх координат вектора х.
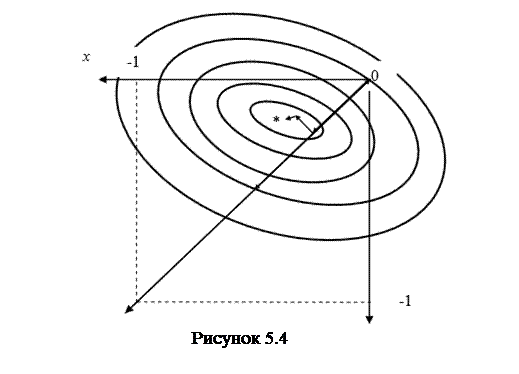
Графічна ілюстрація стратегії пошуку градієнтним методом наведена на рис. 5.4.
 |
Для завершення ітераційного процесу можна вибрати наступний критерій:
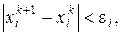 (5.2)
(5.2)
де εі – допустима похибка визначення мінімуму по і-1 координаті. Зокрема, значення усіх εі можуть бути задані однаковими.
За допомогою методу градієнтного спуску мінімум гладких функцій знаходиться значно швидше, ніж при застосуванні покоординатного спуску. Але при цьому одночасно з обчисленням функції f на кожній ітерації градієнтного методу доводиться розраховувати складові градієнта цієї функції. Крім того, збіжність ітераційного процесу (5.1) може бути повільна для функції, що має яружний рельєф.
В околі точки мінімуму складові градієнта функції мають малі значення, що призводить до зростання чутливості ітераційного процесу (5.1) до похибок обчислень і ускладнює пошук на заключному етапі.
5.5. Метод найшвидшого спуску
Метод найшвидшого спуску є модифікацією градієнтного методу. Різниться він способом знаходження довжини кроку а.
Зазначимо, що коли в процесі мінімізації крок а є величиною фіксованою, то метод має назву градієнтного методу з дискретним кроком.
Звернемося до формули (5.1), в якій застосовано параметр а. Цей параметр визначає довжину кроку в напрямку спуска. Виявляється, що під час розв’язання задачі мінімізації цей крок можна змінювати. Такий варіант градієнтного методу називають методом найшвидшого спуску.
Зокрема, відомий підхід до розв’язання задачі мінімізації, коли довжина кроку а вибирається методом дроблення. Ітераційний процес по формулі (5.1) проводять з початковим кроком а до тих пір, поки функція f убиває, тобто виконується умова
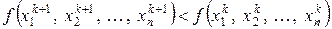 . (5.3)
. (5.3)
При невиконанні цієї умови крок а зменшується вдвічі, розраховуються координати 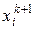 з новим кроком і знову перевіряється умова (5.3). Дроблення кроку продовжується до тих пір, поки не буде виконана умова (5.3). Ітераційний процес продовжується до виконання критерію (5.2).
з новим кроком і знову перевіряється умова (5.3). Дроблення кроку продовжується до тих пір, поки не буде виконана умова (5.3). Ітераційний процес продовжується до виконання критерію (5.2).
Одним із варіантів методу найшвидшого спуску є метод, в якому крок а вибирається за умови мінімізації функції вздовж напрямку, протилежному градієнту. Цей метод запропонував у 1845 році відомий математик О. Коші.
За цим методом передбачається знаходити довжину кроку 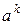 на кожній ітерації виходячи з наступних умов. Для цього розглядають функцію
на кожній ітерації виходячи з наступних умов. Для цього розглядають функцію
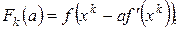
з якої шляхом розв’язання задачі одновимірної мінімізації функції
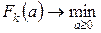
будь-яким ітеративним методом.
Зазначимо, що назва методу найшвидшого спуску не означає, що цей метод дозволяє підійти до точки мінімуму з меншими обчислювальними витратами порівняно з іншими методами.
