Расчет статически определимых балок

Н. Б. ЛЕВЧЕНКО

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

ЧАСТЬ 2

Санкт-Петербург

Министерство образования и науки Российской Федерации

Санкт-Петербургский государственный архитектурно-строительный

университет

Автомобильно-дорожный факультет

Кафедра сопротивления материалов

Н. Б. ЛЕВЧЕНКО

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

Учебное пособие по выполнению расчетно-графических

работ для студентов всех специальностей и форм обучения

ЧАСТЬ 2

Задачи № 12–24, 26, 27

Под редакцией д-ра техн. наук, проф. В. Д. Харлаба

Санкт-Петербург

УДК 539.3/8(07)

Сопротивление материалов:Учебное пособие по выполнению расчетно-графических работ для студентов всех специальностей и форм обучения. Ч. 2 / Н. Б. Левченко; СПбГАСУ. СПб., 2010. с.

В пособии даны краткие сведения из теории, необходимые для решения задач, и приводятся примеры решения задач, входящих в расчетно-графические работы, по теме "Изгиб" с подробными объяснениями.

Ил. 55. Табл. 3. Библиогр. 7 назв.

Рецензенты:

д-р техн. наук, проф. В. З. Васильев (Санкт-Петербургский государственный университет путей сообщения);

д-р техн. наук, проф. В. В. Улитин (Санкт-Петербургский государственный университет низкотемпературных и пищевых технологий)

Рекомендовано Редакционно-издательским советом СПбГАСУ в качестве учебного пособия

© Н. Б. Левченко, 2011

© Санкт-Петербургский государственный

архитектурно-строительный университет, 2011

ОБЩИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ

В процессе изучения курса "Сопротивление материалов" студенты выполняют расчетно-графические работы (РГР). Количество РГР и задач, входящих в каждую из этих работ, зависит от специальности и количества часов, отведенных в учебном плане на изучение курса. Цель РГР – сознательное усвоение теоретического курса и приобретение навыков решения задач, имеющих как академический, так и практический характер.

Данное учебное пособие предназначено для оказания помощи студентам при выполнении расчетно-графических работ. Номера задач, решение которых объясняется в данном пособии, соответствуют номерам задач в методических указаниях [4], по которым студенты выбирают схемы решаемых задач.

В данном пособии приводятся краткие теоретические сведения и основные формулы, необходимые для выполнения задач, объясняются смысл и порядок решения задач. Решение одних задач сопровождается численными расчетами, решение других приведено в общем виде. Ни в коем случае не следует копировать решение задач, не разобравшись со смыслом того, что вы делаете. Пособие не заменяет учебник, поэтому перед выполнением задач прочитайте те разделы учебников, которые приведены в перечне литературы по изучаемой теме. В процессе расчетов обращайте внимание на единицы измерения величин, входящих в формулы. Не забывайте писать, в каких единицах Вы получили результат. Рекомендуемые единицы измерения приведены в перечне используемых обозначений. Все арифметические вычисления следует выполнять с точностью до трех значащих цифр – точностью, достаточной для инженерных расчетов.

Расчетно-графические работы оформляются на одной стороне стандартных листов писчей бумаги формата А-4 (210х297). Перед решением задачи необходимо нарисовать расчетную схему задачи в масштабе в соответствии со своими данными. Решение задачи должно сопровождаться короткими пояснениями, рисунки желательно делать карандашом, на листах должны быть оставлены поля для замечаний преподавателя. После выполнения всех задач, входящих в расчетно-графическую работу, листы с решением следует сброшюровать и снабдить титульным листом.

ИСПОЛЬЗУЕМЫЕ ОБОЗНАЧЕНИЯ

Нагрузки:

– сосредоточенная сила, кН;

– сосредоточенная пара сил (момент), кН×м;

– интенсивность распределенной по длине стержня нагрузки, кН/м.

Обозначение осей:

– продольная ось стержня;

– главные центральные оси инерции поперечного сечения стержня.

Геометрические характеристики поперечного сечения стержня:

A – площадь поперечного сечения, см²;

S_y, S_z – статические моменты относительно осей , см³;

I_y, I_z – осевые моменты инерции относительно осей , см⁴;

I_p– полярный момент инерции, см⁴.

Внутренние усилия:

N – продольная сила, кН;

Q_y , Q_z , (Q)– поперечные силы, кН;

M_y , M_z, (M)– изгибающие моменты кН×м;

M_к – крутящий момент, кН×м.

Напряжения:

(s) – нормальные напряжения, МПа;

(t) – касательные напряжения, МПа;

(s_гл) – главные напряжения, МПа.

Деформации и перемещения:

, (e) – относительные линейные деформации;

(g) – угловые деформации (углы сдвига);

– абсолютная деформация стержня при растяжении-сжатии (пере-мещение точек оси вдоль оси x), см;

v, w – прогибы оси стержня (балки) при изгибе (перемещения точек оси вдоль осей y, z), см;

j – угол поворота оси стержня (балки) при изгибе, рад;

q – угол закручивания стержня (вала) при кручении, рад.

Характеристики материала:

s_пц – предел пропорциональности, МПа;

s_т – предел текучести, МПа;

s_в – временное сопротивление (для хрупких материалов – предел прочности при растяжении, – предел прочности при сжатии), МПа;

[s], [t] – допускаемые напряжения, МПа;

E – модуль упругости, МПа;

n – коэффициент Пуассона;

– коэффициент линейного температурного расширения, 1/град.

ИЗГИБ

Основные понятия и формулы

Изгиб – такой вид деформации стержня, при котором его ось искривляется. Стержень, подверженный изгибу, называется балкой. Конструкция, состоящая из нескольких изгибаемых стержней, соединенных между собой чаще всего под углом 90°, называется рамой. В данном разделе рассматриваются балки и рамы, подверженные плоскому поперечному изгибу. В этом случае вся нагрузка приложена перпендикулярно оси стержня в одной плоскости, совпадающей с плоскостью симметрии поперечного сечения; изогнутая ось является плоской кривой. При плоском поперечном изгибе в балке возникают два вида внутренних усилий: поперечная сила Q и изгибающий момент M. В раме при плоском поперечном изгибе возникают три усилия: продольная N, поперечная Q силы и изгибающий момент M.

Правила знаков для поперечной силы и изгибающего момента зависят от вида рассматриваемой конструкции (прямолинейная балка, рама, криволинейный стержень) и приведены в соответствующих разделах.

Перед тем, как использовать метод сечений для определения внутренних усилий, как правило, надо найти опорные реакции, возникающие в закреплении стержня. Если опорные реакции и внутренние усилия можно найти из уравнений статики, то конструкция называется статически определимой. Чаще всего мы встречаемся с тремя видами опорных закреплений стержней: жестким защемлением (заделкой), шарнирно-неподвижной опорой и шарнирно-подвижной опорой. На рис. 4.1 показаны эти закрепления. Для неподвижной (рис 4.1, б) и подвижной (рис. 4.1, в) опор приведены два эквивалентных обозначения этих закреплений. Напомним, что при действии нагрузки в одной плоскости в заделке возникают три опорных реакции (вертикальная, горизонтальная реакции и сосредоточенный реактивный момент) (рис. 4.1, а); в шарнирно-неподвижной опоре – две реактивные силы (рис. 4.1, б); в шарнирно-подвижной опоре – одна реакция – сила, перпендикулярная плоскости опирания (рис. 4.1, в).

Рис. 4.1. Опорные реакции: а – в заделке; б – в шарнирно-неподвижной опоре; в – в шарнирно-подвижной опоре

После определения опорных реакций внутренние усилия в статически определимых конструкциях определяем с помощью метода сечений. Подробно процесс определения внутренних усилий рассматривается при решении конкретных задач.

Когда внутренние усилия найдены, можно определить напряжения в поперечном сечении изгибаемого стержня. В произвольной точке поперечного сечения возникают нормальное и касательное напряжения, которые для прямолинейных стержней находятся следующим образом:

·* нормальные напряжения в балке определяются по формуле[1]

, (4.1)

где М – величина изгибающего момента в рассматриваемом сечении; z – координата той точки поперечного сечения, в которой определяется s, в главной центральной системе координат; 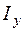– осевой момент инерции относительно главной центральной оси y. Распределение нормальных напряжений по высоте сечения показано на рис. 4.2, а. Ось y, на которой нормальные напряжения равны нулю, называется нейтральной осью;

· касательные напряжения определяются по формуле Журавского[2]:

. (4.2)

В формуле Журавского Q – значение поперечной силы в рассматриваемом сечении; 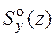– статический момент отсеченной части сечения, зависящий от того, в какой точке определяется касательное напряжение; b(z) – ширина сечения на уровне точки, в которой находится напряжение. Например, на рис. 4.2, б заштрихована отсеченная часть сечения и показана ширина b(z) при определении касательных напряжений в точках, удаленных от оси y на расстояние z.

Рис. 4.2. К определению напряжений при изгибе: а – распределение нормальных напряжений по высоте балки; б – определение отсеченной части сечения в формуле Журавского

Из формулы (4.1) следует, что максимальные нормальные напряжения действуют в точках, наиболее удаленных от оси y (нейтральной оси). Для определения максимальных напряжений из формулы (4.1) можно получить

, (4.3)

где – момент сопротивления балки при изгибе. Для балок круглого и прямоугольного сечений моменты инерции и моменты сопротивления находятся по формулам

; ; (4.4)

; . (4.5)

Закон распределения касательных напряжений, определяемых по формуле Журавского, зависит от формы поперечного сечения. Для балок круглого и прямоугольного сечений касательные напряжения изменяются по высоте балок по закону квадратной параболы (рис. 4.3, а). Они равны нулю в точках, наиболее удаленных от нейтральной оси y, и максимальны в точках, лежащих на оси y. Из формулы (4.2) для балок круглого и прямоугольного сечений следуют формулы для определения максимальных касательных напряжений

; . (4.6)

Очень часто употребляемым сечением для балок является двутавр. Касательные напряжения в полках и стенках двутавровой балки распределяются по разным законам. Наиболее важными при проверке прочности являются касательные напряжения в стенке двутавра. На рис. 4.3, б показана эпюра распределения касательных напряжений в стенке двутавра. Максимальные касательные напряжения в двутавровой балке так же, как и в балках круглого и прямоугольного сечений, действуют в точках, лежащих на нейтральной оси y. Об определении касательных напряжений в двутавре подробно будет сказано при решении задачи о проверке прочности двутавровой балки.

Рис. 4.3. Распределение касательных напряжений по высоте: а – балок круглого и прямоугольного сечений; б – двутавровой балки

Рис. 4.4. "Балочное" напряженное состояние

Основной задачей расчета конструкций является обеспечение их прочности. Известно, что условие прочности в точке тела зависит от материала и от вида напряженного состояния в этой точке. Напряженное состояние произвольной точки стержня при изгибе (балки) показано на рис. 4.4. Назовем такое напряженное состояние "балочным". Это частный случай плоского напряженного состояния, которое отличается от общего случая отсутствием на площадках, перпендикулярных оси z, нормальных напряжений. Для "балочного" напряженного состояния из теорий прочности получены частные формулы проверки прочности. Для хрупких материалов справедливы:

·* вторая теория прочности

; (4.7)

·* теория Мора ( )

; (4.8)

для пластичных материалов используются

·* третья теории прочности

; (4.9)

·* четвертая теория прочности

. (4.10)

РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК

Рекомендуемая литература

Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 2 ( § 2.4–2.5), гл. 4 (§ 4.1, 4.2), гл. 6 (§ 6.1–6.3), гл. 7 (§ 7.1, 7.2), гл. 8 (§ 8.1–8.5, 8.9).

Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 5 (§ 21–25), гл. 15, гл. 8.

Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 5 (§ 5.1–5.5), гл. 7 (§ 7.1–7.8, 7.10, 7.13–7.14), гл. 11 (§ 11.4, 11.5).

Основные определения

Статически определимая балка – балка, в которой опорные реакции, а, следовательно, и внутренние усилия можно найти из одних уравнений статики.

Осваивать расчет статически определимых балок удобно, рассматривая по очереди следующие вопросы:

1. Определение внутренних усилий в балках.

2. Проверка прочности балок.

3. Определение перемещений и проверка жесткости балок.

Решение этих вопросов получим в соответствующих разделах на примере конкретных задач.

Примеры решения задач