Ббк 22.34р30-252.43 1 страница
ФАКУЛЬТЕТ РАДИОФИЗИКИ И ЭЛЕКТРОНИКИ
Кафедра физики
Методические указания к практическим занятиям по курсу "Электричество". часть 1.
Методическое пособие
К практическим занятиям
По электричеству
Для студентов специальностей:
G 31 04 02 “Радиофизика”,
G 31 04 03 “Физическая электроника”
МИНСК
УДК 536.3(075.83)
ББК 22.34р30-252.43
И85
А в т о р ы - с о с т а в и т е л и:
А.Б. Терехович, доцент
А.А. Спиридонов, старший преподаватель
Р е ц е н з е н т
доктор технических наук,
профессор А.С. Михалев
Утверждено Ученым советом
факультета радиофизики и электроники
2002 г., протокол № 12
Методическиеуказания к практическим занятиям по курсу "Электричество". Часть 1.: Метод. пособие к практическим занятиям по электричеству/ Авт.-сост. А.Б. Терехович, А.А. Спиридонов. – Мн.: БГУ, 2002. – 76 с.
Методическое пособие предназначено для студентов 2-го курса факультета радиофизики и электроники.
УДК 536.3(075.83)
ББК 22.34р30-252.43
© БГУ, 2002
1. Электростатическое поле в вакууме
1.1. Электромагнитное поле
В настоящее время известно, что в основе всего разнообразия явлений природы лежат четыре фундаментальных взаимодействия между элементарными частицами — сильное, электромагнитное, слабое и гравитационное. Каждый вид взаимодействия связывается с определенной характеристикой частицы. Например, гравитационное взаимодействие зависит от масс частиц, электромагнитное — от электрических зарядов.
Электромагнитное поле— материальный носитель электромагнитного взаимодействия, в котором участвуют заряженные частицы.
Электрический заряд частицы является одной из основных, первичных ее характеристик. Ему присущи следующие фундаментальные свойства:
1) электрический заряд существует в двух видах: как положительный, так и отрицательный;
2) в любой электрически изолированной системе алгебраическая сумма зарядов не изменяется, это утверждение выражает закон сохранения электрического заряда;
3) электрический заряд является релятивистски инвариантным: его величина не зависит от системы отсчета, а значит, не зависит от того, движется он или покоится.
Иллюстрацией закона сохранения заряда является, например, реакция аннигиляции электрона и позитрона. При столкновении электрона и позитрона рождается две нейтральные частицы — два фотона (γ-кванты — частицы электромагнитного излучения), т.е.
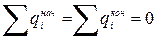 .
.
1.2. Напряженность электрического поля
Принцип суперпозиций.
Согласно современным представлениям, материальным носителем взаимодействия между зарядами является электрическое поле. Всякий электрический заряд q изменяет определенным образом свойства окружающего его пространства — создает электрическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку другой, «пробный», заряд испытывает действие силы.
Опыт показывает, что сила F, действующая на неподвижный точечный пробный заряд q, всегда может быть представлена как
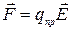 , (1.1)
, (1.1)
где вектор  называютнапряженностью электрического поля в данной точке. Вектор
называютнапряженностью электрического поля в данной точке. Вектор  , как видно из (1.1), можно определить как силу, действующую на единичный положительный неподвижный заряд. Здесь предполагается, что пробный заряд qпр должен быть достаточно малым, чтобы его внесение не вызвало заметного искажения интересующего нас поля (вследствие возможного перераспределения создающих поле зарядов).
, как видно из (1.1), можно определить как силу, действующую на единичный положительный неподвижный заряд. Здесь предполагается, что пробный заряд qпр должен быть достаточно малым, чтобы его внесение не вызвало заметного искажения интересующего нас поля (вследствие возможного перераспределения создающих поле зарядов).
Поле точечного заряда. Из опыта (закон Кулона) непосредственно следует, что напряженность поля неподвижного точечного заряда q на расстоянии r от него можно представить как
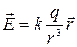 (1.2)
(1.2)
где k — постоянная вид, которой зависит от выбора системы отсчета, в системе СИ 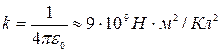 ; ε0 — электрическая постоянная;
; ε0 — электрическая постоянная; 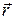 — радиус-вектор, проведенный из центра поля, в котором расположен заряд q, до интересующей нас точки. Напряженность поля
— радиус-вектор, проведенный из центра поля, в котором расположен заряд q, до интересующей нас точки. Напряженность поля  в системе СИ выражается ввольтах на метр (В/м). В зависимости от знака заряда q вектор
в системе СИ выражается ввольтах на метр (В/м). В зависимости от знака заряда q вектор  направлен так же, как и
направлен так же, как и 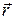 (для положительного заряда), или противоположно ему (для отрицательного заряда).
(для положительного заряда), или противоположно ему (для отрицательного заряда).
По существу, формула (1.2) выражает не что иное, какзакон Кулона, но в «полевой» форме. Вся совокупность экспериментальных фактов показывает, что этот закон справедлив для расстояний от 10 см до нескольких километров, и пока нет никаких оснований ожидать, что этот закон не выполняется и при больших расстояниях.
Принцип суперпозиции. Другой опытный факт, кроме закона (1.2), заключается в том, что напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждый из зарядов в отдельности:
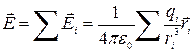 , (1.3)
, (1.3)
где ri — расстояние между зарядом qi и интересующей нас точкой поля.
Это утверждение называют принципом суперпозиции (наложения) электрических полей. Поле точечного заряда является фундаментальным, потому что, используя формулу (1.2) и принцип суперпозиции (1.3), можно расчитать поле любого (!) заряда.
Распределение зарядов. Для упрощения математических расчетов во многих случаях бывает удобно игнорировать тот факт, что заряды имеют дискретную структуру (электроны, ядра), и считать, что они «размазаны» определенным образом и пространстве. Другими словами, удобно заменить истинное распределение точечных дискретных зарядов фиктивным непрерывным распределением. Это позволяет значительно упрощать расчеты, не внося сколько-нибудь значительной ошибки.
При переходе к непрерывному распределению вводят понятие о плотности зарядов — объемной ρ, поверхностной σ и линейной λ. По определению,
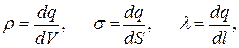 (1.4)
(1.4)
где dq — заряд, заключенный соответственно в объеме dV, на поверхности dS и на длине dl.
C учетом этих распределений формула (1.3) может быть представлена в другой форме. Например, если заряд распределен по объему, то надо заменить qi на dq = ρ dV и ∑ на ∫, тогда
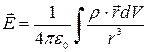 , (1.5)
, (1.5)
где интегрирование проводится по всему пространству, в котором ρ отлично от нуля.
Таким образом, зная распределение зарядов, мы можем полностью решить задачу о нахождении напряженности электрического поля по формуле (1.3), если распределение дискретно, или по формуле (1.5) и аналогично ей, если распределение непрерывно. Этот метод нахождения электрического поля получил название метод непосредственного интегрирования. В общем случае расчет сопряжен со значительными трудностями (правда, не принципиального характера). Действительно, для нахождения вектора  надо вычислить сначала его проекции Еx , Еy , Еz , а это по существу, три интеграла типа (1.5).
надо вычислить сначала его проекции Еx , Еy , Еz , а это по существу, три интеграла типа (1.5).
Методические указания
Для расчета в точке А электрического поля заряда, распределенного в пространстве методом непосредственного интегрирования необходимо:
1) Разбить заряженное тело на бесконечно малые элементы dV (или dS , dl) с элементарным зарядом dq = ρ dV (см. рис. 1);
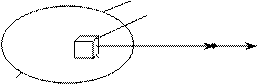 V dV A dq V dV A dq 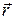 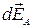 q Рис. 1 q Рис. 1 |
2) Определить напряженность поля 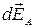 в точке А, создаваемого точечным зарядом dq:
в точке А, создаваемого точечным зарядом dq:
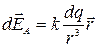 ;
;
3) По принципу суперпозиций результирующее поле в очке А находится интегрированием по всему объему пространства V, где находится заряд:
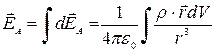 .
.
Замечание. Для вычисления 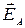 обычно переходим к его проекциям на соответствующие оси выбранной системы координат. Так, в декартовой системе координат это предполагает, в общем случае, нахождение трех интегралов:
обычно переходим к его проекциям на соответствующие оси выбранной системы координат. Так, в декартовой системе координат это предполагает, в общем случае, нахождение трех интегралов:

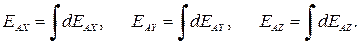
Пример 1.1 Заряд q > 0 равномерно распределен по тонкому кольцу радиусом R. Найти напряженность Е электрического поля на оси кольца как функцию расстояния z от его центра.
Решение. Легко сообразить, что в данном случае вектор Е должен быть направлен по оси кольца (рис. 2). Выделим на кольце элемент dl. Запишем выражение для составляющей 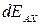 от этого элемента в точке А:
от этого элемента в точке А:
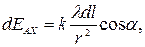
где λ = q/2πR. Для всех элементов кольца r и R будут одними и теми же, поэтому интегрирование этого выражения сводится просто к замене dl на q.
dl r R 0 α  x x 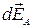 Рис.2 Рис.2 |
В результате получаем:
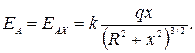
Видно, что при x » а поле Е = q/4πε0x2 , т. е. на больших расстояниях эта система ведет себя как точечный заряд.
Пример 1.2 Сфера радиуса R заряжена с поверхностной плотностью 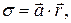 где
где 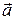 — постоянный вектор;
— постоянный вектор; 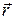 — радиус-вектор точки сферы относительно ее центра. Найти напряженность поля в центре сферы.
— радиус-вектор точки сферы относительно ее центра. Найти напряженность поля в центре сферы.
Решение. Выберем систему декартову координат таким образом, чтобы вектор 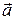 был направлен вдоль оси Z (см. рис. 3).
был направлен вдоль оси Z (см. рис. 3).
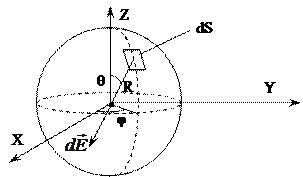 |
Рис. 3
Разобьем сферическую поверхность на элементарные площадки dS, содержащие элементарные заряды dq=σdS. Поле dq в точке О имеет вид:
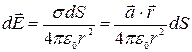
Перейдем для удобства дальнейших расчетов к сферическим координатам:
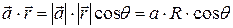 ;
;
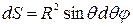 .
.
Тогда поле dq будет иметь вид:
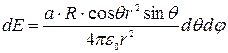 .
.
Соответствующие проекции на оси координат будут иметь вид:
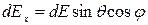 ;
;
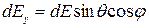 ;
;
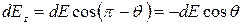 .
.
Используя принцип суперпозиций, имеем проекции результирующего поля в точке О:
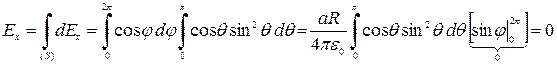 ;
;
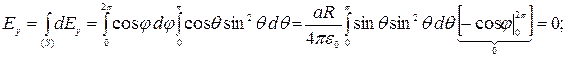
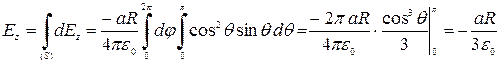 .
.
Окончательно можно записать поле в центре сферы:
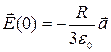 .
.
1.3. Теорема Гаусса
Поток вектора  . Для большей наглядности воспользуемся геометрической картиной описания электрического поля (с помощью линий вектора
. Для большей наглядности воспользуемся геометрической картиной описания электрического поля (с помощью линий вектора  ) и еще, для упрощения рассуждений, будем считать, что густота линий
) и еще, для упрощения рассуждений, будем считать, что густота линий  равна модулю вектора
равна модулю вектора  . Тогда число линий, пронизывающих элементарную площадку
. Тогда число линий, пронизывающих элементарную площадку 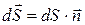 , единичная нормаль
, единичная нормаль 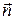 которой составляет угол α с вектором
которой составляет угол α с вектором  , определяется согласно рисунку 4 как
, определяется согласно рисунку 4 как 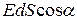 . Эта величина и есть элементарный поток
. Эта величина и есть элементарный поток 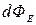 вектора
вектора  сквозь площадку dS:
сквозь площадку dS:
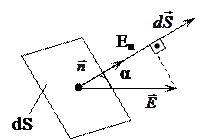 Рис. 4 Рис. 4 |
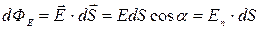 , (1.6)
, (1.6)
где Еп— проекция вектора  на нормаль
на нормаль 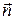 к площадке
к площадке 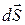 . Выбор направления вектора
. Выбор направления вектора 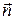 (а следовательно, и
(а следовательно, и 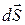 ) условен, его можно было направить и в противоположную сторону.
) условен, его можно было направить и в противоположную сторону.
Если имеется некоторая произвольная поверхность S, то поток вектора  сквозь нее равен
сквозь нее равен
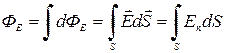 . (1.7)
. (1.7)
Эта величина алгебраическая: она зависит не только от конфигурации поля  , но и от выбора направления нормали. В случае замкнутых поверхностей принято нормаль
, но и от выбора направления нормали. В случае замкнутых поверхностей принято нормаль 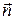 брать наружу области, охватываемой этими поверхностями, т. е. выбирать внешнюю нормаль, что в дальнейшем будет всегда и подразумеваться. Тогда поток через замкнутую поверхность будем обозначать
брать наружу области, охватываемой этими поверхностями, т. е. выбирать внешнюю нормаль, что в дальнейшем будет всегда и подразумеваться. Тогда поток через замкнутую поверхность будем обозначать
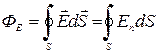 .
.
Понятие потока в равной степени относится к любому векторному полю.
Теорема Гаусса. Поток вектора  сквозь произвольную замкнутую поверхность S обладает удивительным и замечательным свойством: он зависит только от алгебраической суммы зарядов, охватываемых этой поверхностью, а именно:
сквозь произвольную замкнутую поверхность S обладает удивительным и замечательным свойством: он зависит только от алгебраической суммы зарядов, охватываемых этой поверхностью, а именно:
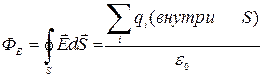 (1.8)
(1.8)
Это выражение и есть теорема Гаусса: поток вектора  сквозь замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной па
сквозь замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной па 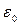 .
.
Если заряды распределены непрерывно с объемной плотностью, зависящей от координат, в этом случае можно считать, что каждый элементарный объем dV содержит «точечный» заряд ρ dV . Тогда выражение (1.8) будет иметь вид:
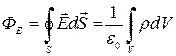 , (1.9)
, (1.9)
где интегрирование проводится только по объему V, заключенному внутри замкнутой поверхности S.
Необходимо обратить внимание на следующее важное обстоятельство: в то время как само поле  зависит от конфигурации всехзарядов, поток вектора
зависит от конфигурации всехзарядов, поток вектора  сквозь произвольную замкнутую поверхность S определяется только алгебраической суммой зарядов внутриповерхности S. Это значит, что если передвинуть заряды, то поле
сквозь произвольную замкнутую поверхность S определяется только алгебраической суммой зарядов внутриповерхности S. Это значит, что если передвинуть заряды, то поле  изменится всюду, в частности и на поверхности S, изменится и поток вектора
изменится всюду, в частности и на поверхности S, изменится и поток вектора  через S. Однако если передвижка зарядов произошла без пересечения поверхности S, поток вектора
через S. Однако если передвижка зарядов произошла без пересечения поверхности S, поток вектора  через эту поверхность останется прежним,хотя, повторяем, само поле
через эту поверхность останется прежним,хотя, повторяем, само поле  может измениться, причем весьма существенно.
может измениться, причем весьма существенно.
Применение теоремы Гаусса.При использовании теоремы Гаусса для расчета электрических полей нужно учитывать, что:
1) рассчитать можно только поле, которое обладает специальной симметрией (чаще всего плоской, цилиндрической или сферической).
2) симметрия и конфигурация поля должны быть такими, чтобы можно было найти достаточно простую замкнутую поверхность S (называемую гауссовой поверхностью), такую, чтобы отдельные ее части Si были параллельны вектору (тогда
(тогда 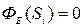 ) или отдельные ее части Sj были перпендикулярны
) или отдельные ее части Sj были перпендикулярны  и напряженность на них была постоянна по модулю (тогда
и напряженность на них была постоянна по модулю (тогда 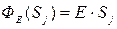 ).
).
Если этого нет, задачу о нахождении поля приходится решать помощью метода непосредственного интегрирования или с помощью других методов, с которыми мы ознакомимся ниже.
Методические указания
Для расчета электрического поля, обладающего специальной симметрией, с помощью теоремы Гаусса необходимо:
1) качественно определить характер электрического поля заряженного тела;
2) удобным образом выбрать гауссову поверхность S (см. п.2 Применение теоремы Гаусса);
3) результирующий поток через поверхность S рассчитать как алгебраическую сумму потоков через поверхности Si , составляющие ее:
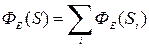 .
.
4) если заряды распределены непрерывно с объемной плотностью ρ, зависящей от координат, разбить заряженное тело на бесконечно малые объемы dV с элементарным зарядом dq = ρ dV . Тогда 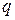 (внутри S)
(внутри S) 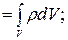
5) для расчета  записать теорему Гаусса:
записать теорему Гаусса:
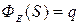 (внутри S).
(внутри S).
Пример 1.3. Рассчитать напряженность поля прямой бесконечной нити, равномерно заряженной с линейной плотностью λ, в точке А, удаленной от нити на расстояние r0 .
Решение. 1-й способ. Применим теорему Гаусса для расчета напряженности поля (поле цилиндрической симметрии). В силу симметрии поля вектор напряженности  в любой точкенормален цилиндрической поверхности, проходящей через эту точку (рис. 5).
в любой точкенормален цилиндрической поверхности, проходящей через эту точку (рис. 5).
| l λ A r Рис.5 |
 В Y dl C A r dα α О X D r0 Рис. 6 В Y dl C A r dα α О X D r0 Рис. 6 |
Ось симметрии этой поверхности совпадает с нитью. Поэтому в качестве замкнутой поверхности выберем цилиндр длиной l с осью симметрии, совпадающей с нитью, боковая поверхность которого проходит через точку А.
Поток вектора  через боковую поверхность цилиндра
через боковую поверхность цилиндра
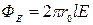 ,
,
а электрический заряд, расположенный внутри цилиндра
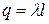 .
.
Тогда по теореме Гаусса имеем:
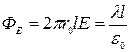 .
.
Отсюда определяем искомую напряженность:
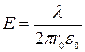 .
.
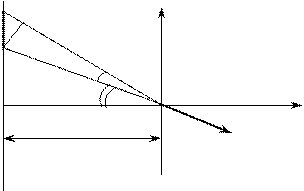
2-й способ (Метод непосредственного интегрирования). Разделим нить на столь малые элементы, в пределах которых можно считать заряд точечным. Рассмотрим один такой элемент длиной dl с зарядом dq=λdl (рис. 6).
В точке О элементарная напряженность поля этого заряда
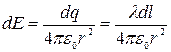 .
.
Из треугольника ADO находим: 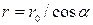 . Так как
. Так как 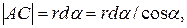 то из треугольника ABC определяем:
то из треугольника ABC определяем:
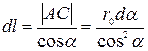 .
.
Подставляя значения r, dα , получаем:
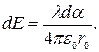
Проекции вектора 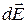 наоси ОX и ОY:
наоси ОX и ОY:
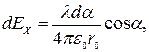
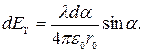
Отсюда после интегрирования получаем:
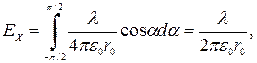
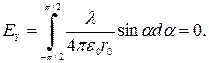
Окончательно получаем:
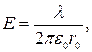
что совпадает с выражением, полученным с помощью теоремы Гаусса.
Пример 1.4Система состоит из равномерно заряженной сферы радиусом R и окружающей среды, заполненной зарядом с объемной плотностью ρ = α/r, где α — положительная постоянная, r — расстояние от центра сферы. Найти заряд сферы, при котором напряженность  электрического поля вне сферы не будет зависеть от r. Чему равно Е?
электрического поля вне сферы не будет зависеть от r. Чему равно Е?
Решение. Пусть искомый заряд сферы равен q, тогда, воспользовавшись теоремой Гаусса, запишем для сферической поверхности радиусом r>R (снаружи сферы с зарядом q):
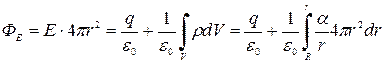 .
.
Проинтегрировав, преобразуем предыдущее уравнение к виду: 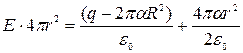 .
.
Напряженность Е не зависит от r при условии, когда выражение в скобках равно нулю. Отсюда
q = 2παR2 и Е =α/2ε0.
Выражения для напряженности полей заряженных тел (в вакууме), обладающих специальной симметрией, рассчитанных по теореме Гаусса.
| Равномерно заряженная с линейной плотностью λбесконечная нить (поле цилиндрической симметрии) | 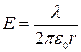 (r — расстояние от нити по перпендикуляру к ней) (r — расстояние от нити по перпендикуляру к ней) |
| Равномерно заряженная зарядом q по поверхности сфера радиусом R (поле сферической симметрии) | 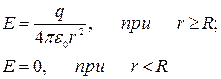 (r — расстояние от центра сферы) (r — расстояние от центра сферы) |
| Заряд равномерно распределен с объемной плотностью ρ по объему шара радиуса R (поле сферической симметрии) | 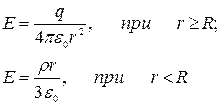 (r — расстояние от центра шара) (r — расстояние от центра шара) |
| Равномерно заряженная с поверхностной плотностью σбесконечная поверхность (поле плоской симметрии) | 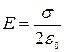 (однородное поле во всем пространстве) (однородное поле во всем пространстве) |
Теорема Гаусса в дифференциальной форме.Замечательное свойство электрического поля, которое выражает собой теорема Гаусса, побуждает представить эту теорему в иной форме, расширяющей ее возможности как инструмента исследования и расчета.
В отличие от формы (1.8) — ее называют интегральной — мы будем искать дифференциальную форму теоремы Гаусса, в которой устанавливается связь между объемной плотностью заряда ρ и изменениями напряженности Е в окрестности данной точки пространства.
Для этого представим сначала заряд q в объеме V, охватываемом замкнутой поверхностью S, как 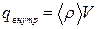 , где
, где 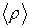 — среднее по объему V значение объемной плотности заряда. Затем подставим это выражение в уравнение (1.8) и разделим обе части его на V. В результате получим:
— среднее по объему V значение объемной плотности заряда. Затем подставим это выражение в уравнение (1.8) и разделим обе части его на V. В результате получим:
