Структурна стійкість систем управління

У попередніх лекціях було показано, що стійкість системи залежить як від виду характеристичного рівняння системи, так і від конкретних числових значень коефіцієнтів рівняння. Існують системи, які нестійкі при будь-яких значеннях параметрів. Такі системи називають структурно нестійкими. Структурно нестійку систему можна зробити стійкої, змінивши її структуру. У структурно нестійкої системи в просторі будь-яких її параметрів області стійкості не існує.

Розглянемо одноконтурну систему, що містить одну інерційну ланку й дві ідеальних інтегруючих. Характеристичне рівняння замкнутої системи має вигляд:

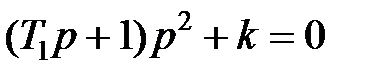(1)

і не містить доданок с p у першому ступені. Очевидно, що в цьому випадку не виконується необхідна умова стійкості - умова позитивності коефіцієнтів, і ніякі варіації параметрів k і Т₁ не можуть привести до появи що складається с р у першій ступені. Отже, ця система структурно нестійка.

Існують ланки, які, як правило, погіршують стійкість системи, і ланки, які майже завжди поліпшують стійкість. До першої групи відносять ланки:

- ідеальне інтегруюче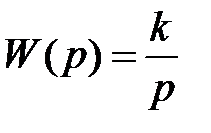

- нестійка статична ланка першого порядку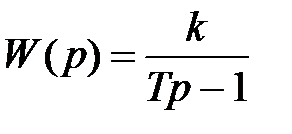

- консервативна (ідеальна коливальна ланка)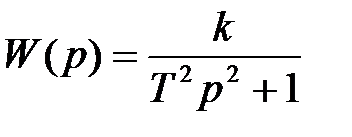

Ланками, що поліпшують стійкість системи, є ланки, що форсують. Звичайно застосовують ланки, що форсують, першого порядку:

.

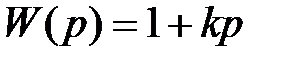Широко застосовуваний у промисловій автоматиці пропорційно-інтегральний закон регулювання відповідає послідовному з'єднанню ідеального інтегруючої ланки й ланки, що форсує, першого порядку:

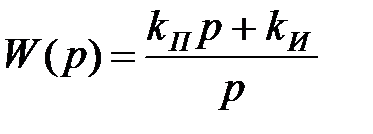
Вплив цього закону на стійкість двояке: при більших значеннях коефіцієнта інтегральної складової k_и стійкість гірше, при більших значеннях коефіцієнта k_п - краще.

Розглянемо загальні умови структурної стійкості одноконтурної системи. Характеристичне рівняння системи в загальному випадку має вигляд:

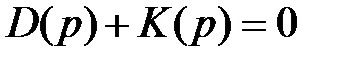, (2)

де 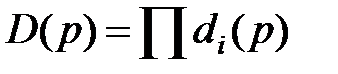- добуток знаменників передатних функцій окремих ланок, що входять у контур системи;

К(р) - добуток чисельників цих же функцій.

Умови структурної стійкості залежать від загального порядку п характеристичного рівняння (2) і від виду поліномів D(р) і К(р). У поліном D(р) входять знаменники «поганих» ланок (що погіршують стійкість), а в поліном К(р) - чисельники «гарних» - ланок, що форсують. Позначимо:

q - число ідеальних інтегруючих ланок;

t - число нестійких статичних ланок першого порядку;

r - число консервативних ланок вхідних у систему.

Якщо ланок, що форсують, у контурі ні, тобто К(р) = k (де k - загальний передатний коефіцієнт розімкнутого контуру), то умова структурної стійкості системи виражається у вигляді двох нерівностей:

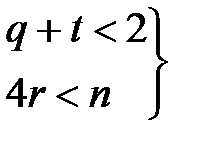
Вплив передатного коефіцієнта розімкнутого контуру системи на стійкість.

Для одноконтурних систем коефіцієнт k входить у вираження АФЧХ 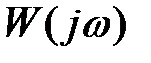як множник:

,

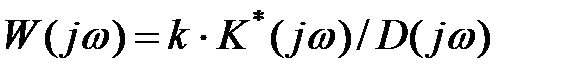де .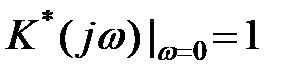

Це означає, що довжини вектора 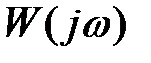при всіх значеннях пропорційні коефіцієнту k. При збільшенні коефіцієнта k АФЧХ розширюється (мал. а)і наближається до критичної крапки (-1; j0). Отже, збільшення передатного коефіцієнта розімкнутого контуру приводить до порушення стійкості системи.

Це правило справедливо для більшості реальних систем, у яких АФЧХ має форму плавної спіралі (мал. а).Однак існують системи, у яких АФЧХ має дзьбоподібну форму (мал. б). У таких системах до порушення стійкості може· привести не тільки збільшення, але й зменшення передатного коефіцієнту.

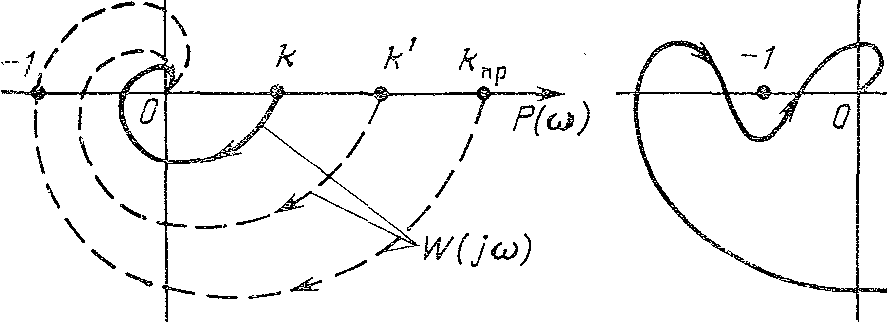
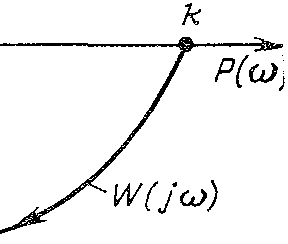
а) б)

Значення передатного коефіцієнта, при якому АФЧХ проходить через крапку (- 1; j0), називають граничним або критичним.

В існуванні граничного коефіцієнта можна переконатися й за допомогою критерію Михайлова. Дійсно, у простих одноконтурних систем коефіцієнт k входить тільки в коефіцієнт а_п характеристичного рівняння, причому, для статичних систем а_п = 1 + k, а для астатичних а_п = k. Якщо збільшувати коефіцієнт k, то буде збільшуватися тільки коефіцієнт а_п, і характеристична крива 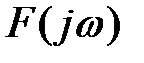без деформації буде переміщатися вправо (мал.).Очевидно, що при деякому граничному значенні коефіцієнта а_п, а отже, і коефіцієнта k, крива 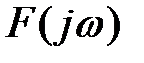пройде через початок координат, тобто система буде на границі стійкості.

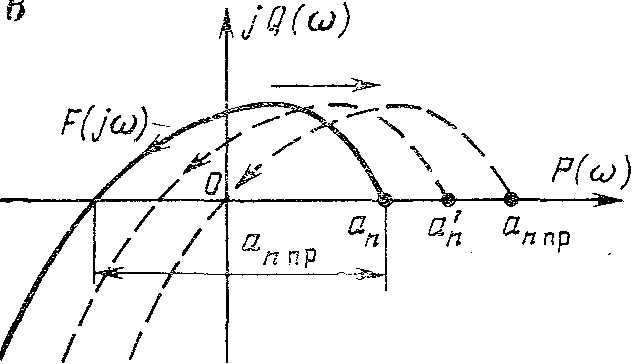
Таким чином, установлена одна з найважливіших у ТАУ закономірностей:

чим більше загальний передатний коефіцієнт розімкнутого контуру системи регулювання, тим ближче замкнута система до границі стійкості.

Граничне значення передатного коефіцієнта залежить від співвідношення постійних часу ланок, що утворять контур системи. Розглянемо, наприклад, статичну систему, що складається із трьох інерційних ланок першого порядку з передатними коефіцієнтами k₁, k₂, k₃ і постійними часу Т₁,Т₂, Т₃. Характеристичне рівняння такої системи

,

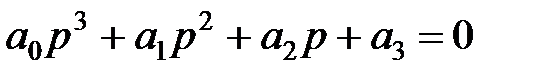де ; ; ; .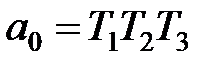

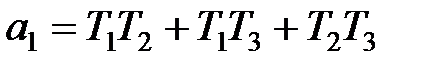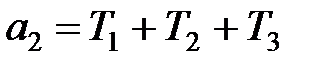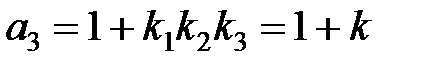Відповідно до критерію Гурвица система третього порядку буде перебувати на границі стійкості при .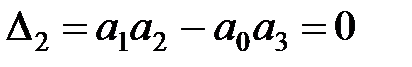

Підставивши в цю умову коефіцієнти характеристичного рівняння, одержимо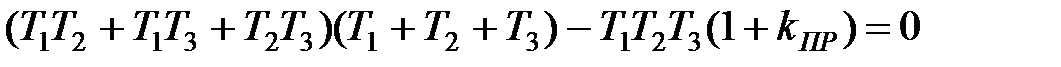

Вирішивши цю рівність відносно k_пр і виконавши деякі додаткові перетворення (ділення на а₀), одержимо вираження для граничного коефіцієнта передачі:

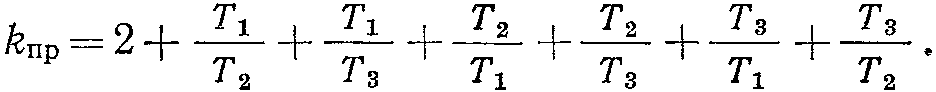
Аналізуючи дану залежність можна довести, що граничний коефіцієнт тим більше, чим більше різниця між двома постійними часу (наприклад, Т₁ і Т₂), що найбільш різняться, і чим ближче третя постійна часу (Т₃) до середньоарифметичного значення двох перших.

На підставі вираження можна сформулювати важливе практичне правило:

граничне значення передатного коефіцієнта системи залежить від співвідношення постійних часу й не залежить від їхніх абсолютних значень.

Наведене правило справедливо для систем будь-якого порядку, і, тому, завжди при конструюванні систем прагнуть якнайбільше «розсунути» постійні часу. Однак зміна постійних часу з метою збільшення передатного коефіцієнта й поліпшення точності системи в багатьох випадках виявляється неможливим або недоцільним. Дійсно, при конструюванні елементів системи звичайно вживають заходів, спрямовані на максимальне зменшення постійних часу, а тому подальше їхнє зменшення, як правило, неможливо. Збільшення ж постійних часу недоцільно, тому що веде до погіршення швидкодії всієї системи.

ОЦІНКА ЯКОСТІ УПРАВЛІННЯ

Дослідження системи автоматичного управління на стійкість дозволяє визначити можливість або неможливість її функціонування. Однак дані дослідження не дозволяють оцінити ефективність використання цієї системи, навіть якщо вона виявилася стійкою. Для оцінки ефективності функціонування САУ використовують показники якості систем керування.

У ТАУ термін «якість системи», «якість управління» використовують у більше вузькому змісті: розглядають тільки статистичні й динамічні властивості системи. Ці властивості визначають точність підтримки керованої величини на заданому рівні в сталих і перехідних режимах. Кількісне вираження цих властивостей утворять показники якості управління.

Раніше була розглянута точність системи в сталих режимах, що є однієї з найважливіших характеристик якості управління. Тепер будуть розглянуті показники якості, що характеризують точність системи в перехідних режимах (несталий динамічний режим).

Точність системи в перехідних режимах оцінюють за допомогою прямих і непрямих показників якості.

Прямі показники якості визначають за графіком перехідного процесу, що виникає в системі при східчастому зовнішньому впливі. Непрямі показники якості визначають по частотних характеристиках системи або по розподілі коренів характеристичного рівняння. До особливої категорії показників якості відносять інтегральні оцінки, які обчислюють або безпосередньо по перехідній функції системи, або за коефіцієнтами передатної функції системи.

При самій загальній оцінці якості, насамперед, звертають увагу на форму перехідного процесу. Розрізняють наступні типові перехідні процеси: коливальний (1), аперіодичний з перерегулюванням (2), монотонний аперіодичний, (3).

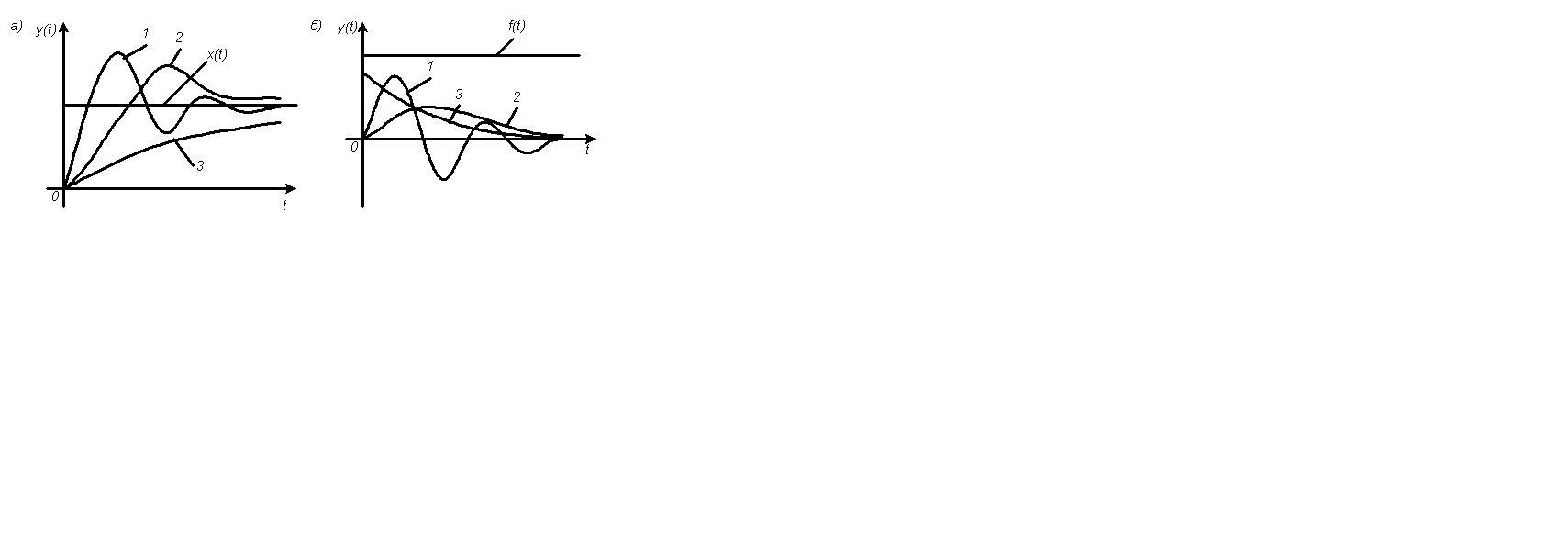
Рисунок 1. Типові перехідні процеси (а – за завданням; б – за збурюванням)

Кожний з типових перехідних процесів має свої переваги й недоліки, і переваги тій або іншій формі процесу роблять із урахуванням особливостей керованого об'єкта.

Прямі показники якості

На графіку перехідних процесів, викликаних східчастою зміною впливів, що задає x(t) і що обурює f(t), за початок відліку для вихідної величини y(t) прийняте значення y(-0), що було до подачі східчастого впливу.

Перерегулювання s - величина, рівна відношенню першого максимального відхилення y_м керованої величини y(t) від її сталого значення y(¥) до цього сталого значення y(¥):

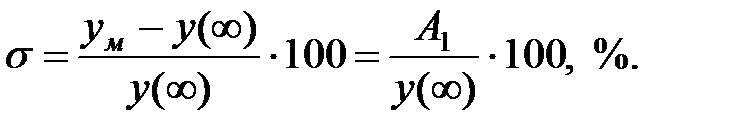
Якість управління вважається задовільною, якщо перерегулювання не перевищує 30...40%.

Для перехідних процесів, викликаних впливом, що обурює, f(t) на вході OУ, перерегулювання можна визначити як відношення першого негативного максимального відхилення А₂ до першого позитивного максимального відхилення А₁:

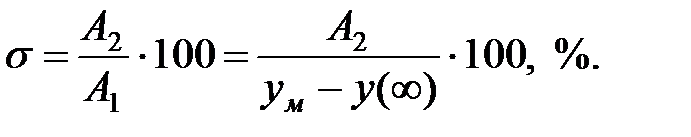
Показник перерегулювання, що обчислюється по даній формулі для перехідних процесів по каналі збурювання, називають також коливальністю.

Необхідно відзначити, що й саме перше максимальне відхилення y_м, що виникає від збурювання на вході об'єкта, є показником якості. При формуванні вимог до системи вказують припустиме значення максимального відхилення (безпосередньо в одиницях виміру керованої величини).

Рисунок 2. Прямі показники якості регулювання

Тривалість перехідного процесу (час регулювання) t_п – інтервал часу від моменту додатка східчастого впливу до моменту, після якого відхилення керованої величини y(t) від її нового сталого значення y(¥) стають менше деякого заданого числа d_п, тобто до моменту, після якого виконується умова êy(t) - y(¥)ê £ d_п.

У промисловій автоматиці величину d_п звичайно приймають рівної 5% від сталого значення y(¥): d_п = 0,05y(¥).

При оцінці тривалості перехідних процесів, викликаних одиничним впливом, що обурює, f(t) на вході об'єкта величину d_п приймають 5% від значення передатного коефіцієнта об'єкта k₀: d_п = 0,05k₀.

Ступінь загасання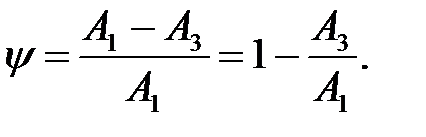

де 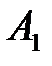й 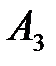- сусідні максимальні відхилення одного знаку.

Інтенсивність загасання коливань у системі вважається задовільної, якщо ( = 0,75...0,95.

Коливальність N – число переходів керованої величини y(t) через її стале значення y(¥) за час перехідного процесу t_п.

При проектуванні систем найчастіше допускають N = 1...2…2,а іноді й до 3...4, але в деяких випадках коливання в системі не припустимі.

Додаткові часові показники якості:

- Час наростання t_н;

- Час досягнення першого максимуму t_м;

- Період загасаючих коливань Т_з.

Ці показники разом з t_п характеризують швидкодію системи регулювання.

Три головних показники якості – перерегулювання s, перше максимальне відхилення y_м і тривалість перехідного процесу t_п - тісно зв'язані між собою. Вони залежать від всіх параметрів системи, але найбільше сильно – від передатного коефіцієнта k розімкнутої системи. Причому, зі збільшенням цього коефіцієнта максимальне відхилення по каналі збурювання завжди зменшується (рис.3, а), максимальне відхилення за каналом впливу, що задає, завжди збільшується (рис.3, б) а перерегулювання й тривалість перехідного процесу, як правило, збільшуються (рис.3). Відшукання оптимального компромісу між цими двома суперечливими
тенденціями є однієї з основних завдань синтезу САУ.

Рисунок 3. Вплив передатного коефіцієнта розімкнутої системи на показники перехідного процесу

а – за впливом, що обурює; б - за впливом, що задає

Непрямі показники якості

Частотні показники

Частотні показники визначають по частотних характеристиках замкнутого й розімкнутого контуру системи.

АЧХ замкнутої системи.

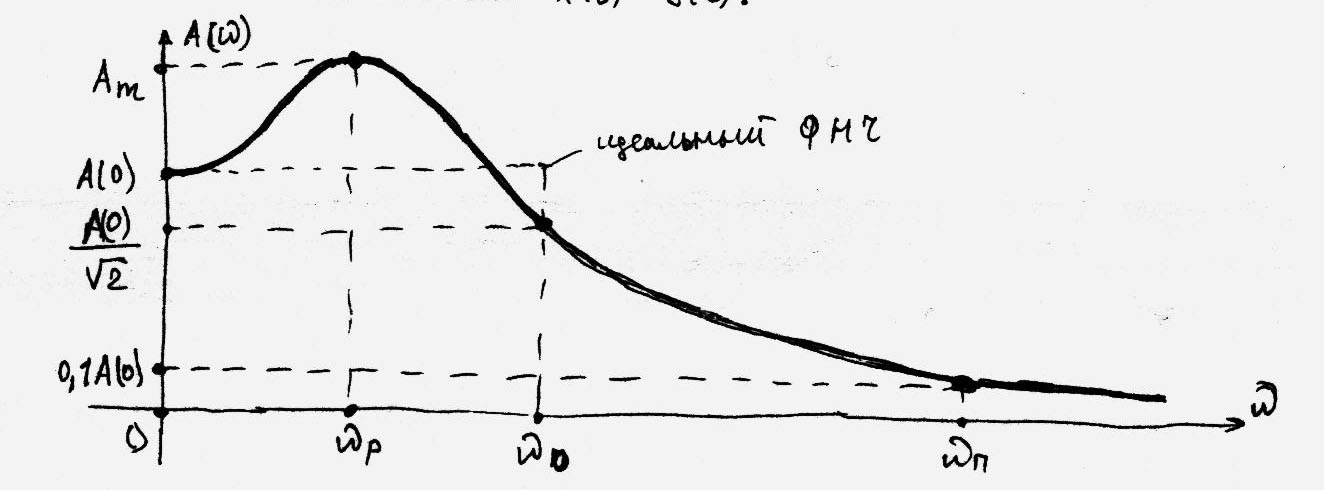
Частотний показник коливальності М: 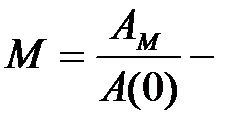це відношення максимуму АЧХ А_М до початкового значення АЧХ А(0).

Чим більше 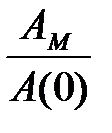, тим сильніше коливальність системи (більше перерегулювання 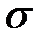), і як наслідок більше тривалість перехідного процесу t_п. Якість системи вважається задовільною, якщо показник М = 1,1...1…1,5

Непрямими частотними показниками швидкодії системи є характерні частоти.

- резонансна частота ω_р – відповідає піку АЧХ, близька до частоти коливань у перехідному процесі;

- смуга пропущення системи – це інтервал частот від ω=0 до ω₀, при якій виконується умова 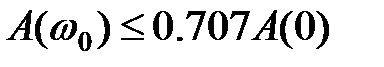. Смуга пропущення не повинна бути занадто широкою, інакше система буде відтворювати високочастотні перешкоди. У той же час, чим менше смуга пропущення системи, тим більше інерційна система (більший час перехідного процесу).