Применение теоремы об изменении кинетической энергии при изучения движения механической системы
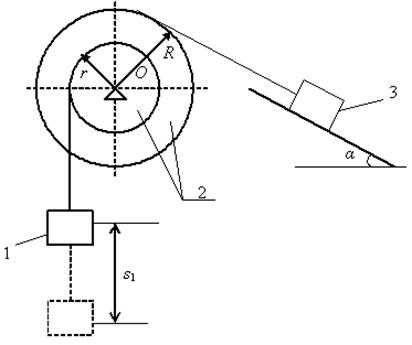
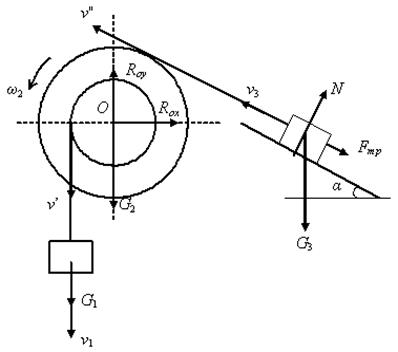
Задача 2. Механическая система под действием сил тяжести приходит в движение из состояния покоя. Учитывая трение скольжения тела 3, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость и ускорение тела 1 в тот момент, когда пройденный им путь станет равным s (рис. 3.70). В задаче принять:
Решение. На механическую систему действуют активные силы 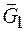 ,
, 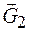 ,
, 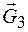 . Применяя принцип освобождения от связей системы, покажем реакции шарнирно-неподвижной опоры 2 и шероховатой наклонной поверхности. Направления скоростей тел системы изобразим с учетом того, что тело 1 спускается.
. Применяя принцип освобождения от связей системы, покажем реакции шарнирно-неподвижной опоры 2 и шероховатой наклонной поверхности. Направления скоростей тел системы изобразим с учетом того, что тело 1 спускается.
Задачу решим, применяя теорему об изменении кинетической энергии механической системы:
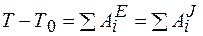 ,
,
где Т и 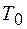 – кинетическая энергия системы в начальном и конечном положениях;
– кинетическая энергия системы в начальном и конечном положениях; 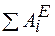 - алгебраическая сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное;
- алгебраическая сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное; 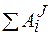 - сумма работ внутренних сил системы на том же перемещении.
- сумма работ внутренних сил системы на том же перемещении.
Для рассматриваемой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями,
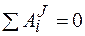 .
.
Так как в начальном положении система покоилась, то 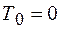 . Следовательно,
. Следовательно,
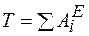 .
.
а)
б)
Кинетическая энергия системы представляет собой сумму кинетических энергий тел 1, 2, 3
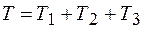 .
.
Кинетическая энергия груза 1, движущегося поступательно, равна:
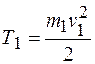 .
.
Кинетическая энергия блока 2, совершающего вращение вокруг оси Оz, перпендикулярной плоскости чертежа,
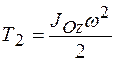 .
.
Кинетическая энергия тела 3 в его поступательном движении
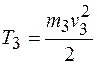 .
.
Таким образом,
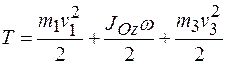 .
.
Выражение кинетической энергии содержит неизвестные скорости всех тел системы. Начать определение необходимо с 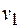 . Избавимся от лишних неизвестных, составив уравнения связей.
. Избавимся от лишних неизвестных, составив уравнения связей.
Уравнения связей это не что иное, как кинематические соотношения между скоростями и перемещениями точек системы. При составлении уравнений связей выразим все неизвестные скорости и перемещения тел системы через скорость и перемещение груза 1.
Скорость любой точки обода малого радиуса 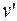 равна скорости тела 1, а также произведению угловой скорости тела 2 и радиуса вращения r
равна скорости тела 1, а также произведению угловой скорости тела 2 и радиуса вращения r
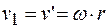 .
.
Отсюда выразим угловую скорость тела 2
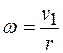 . (а)
. (а)
Вращательная скорость любой точки обода блока большого радиуса 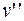 , с одной стороны, равна произведению угловой скорости блока и радиуса вращения, а с другой – скорости тела 3
, с одной стороны, равна произведению угловой скорости блока и радиуса вращения, а с другой – скорости тела 3
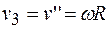 .
.
Подставив значение угловой скорости, получим:
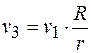 . (б)
. (б)
Проинтегрировав при начальных условиях выражения (а) и (б), запишем соотношение перемещений точек системы:
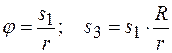 . (в)
. (в)
Зная основные зависимости скоростей точек системы, вернемся к выражению кинетической энергии и подставим в него уравнения (а) и (б):
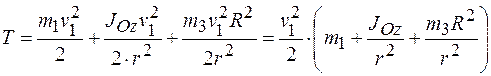 .
.
Момент инерции тела 2 равен:
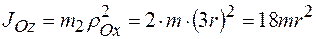 .
.
Подставляя значения масс тел и момента инерции тела 2, запишем
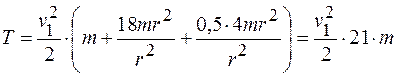 .
.
Определение суммы работ всех внешних сил системы на заданном перемещении.
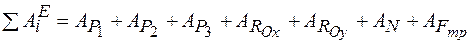 .
.
Работа силы тяжести тела 1
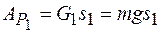 .
.
Работа сил 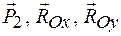 равна нулю, так как эти силы приложены к неподвижной точке.
равна нулю, так как эти силы приложены к неподвижной точке.
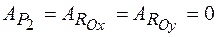 .
.
Работа силы тяжести тела 3
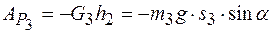 .
.
Работа нормальной реакции тела 3 равна нулю, так как сила перпендикулярна направлению движения
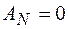 .
.
Работа силы трения скольжения
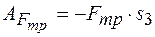 ,
,
так как
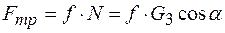 ,
,
тогда
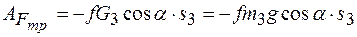 .
.
Сумма работ внешних сил
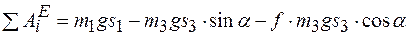 .
.
Подставляя значения масс тел, соотношения перемещений (в) и числовые параметры, запишем:
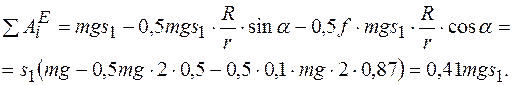
Теперь согласно теореме об изменении кинетической энергии механической системы приравняем значения Т и 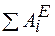
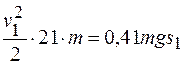 . (г)
. (г)
Скорость тела 1 получим из выражения (г)
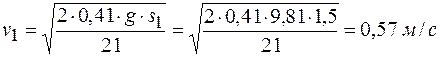 .
.
Ускорение тела 1 можно определить, продифференцировав по времени равенство (г):
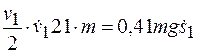 ,
,
где 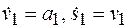 .
.
Тогда
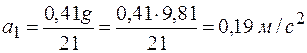 .
.
Сопротивление материалов
Сопротивление материалов — это наука об инженерных методах расчета на прочность, жесткость и устойчивость элементов конструкций.
Способность конструкции (или отдельного ее элемента) выдерживать заданную нагрузку не разрушаясь и без появления остаточных деформаций называют прочностью.
Способность конструкции (или отдельного элемента) сохранять исходную форму в заданных (обычно весьма малых) пределах называется жесткостью.
Способность конструкции (или отдельного элемента) сохранять первоначальную форму упругого равновесия называют устойчивостью.
Напряжением в точке называется величина внутренних сил, приходящихся на единицу площади.
Существует 2 вида напряжений:
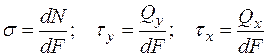 ,
,
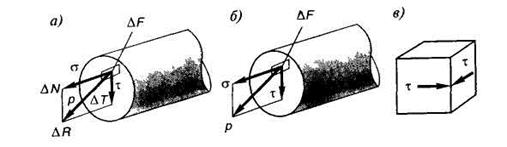
Рис. 1.
причем  (сигма) — нормальное напряжение,действует по нормали (перпендикуляру) к площадке; а
(сигма) — нормальное напряжение,действует по нормали (перпендикуляру) к площадке; а  (тау) — касательные напряжения, они скользят по площадке, касаются ее (рис. 1. в).
(тау) — касательные напряжения, они скользят по площадке, касаются ее (рис. 1. в).
Напряжения измеряются в Н/м2 (Па) и МПа.
В сопромате различают следующие виды деформации.
Центральное растяжение (сжатие) возникает в случае, когда стержень нагружен силами, совпадающими по направлению с его осью (рис. 2). В этом случае из шести внутренних силовых факторов пять равны нулю и только продольная сила 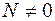 .
.
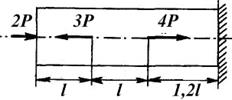
Рис. 2
На растяжение, сжатие работают многие элементы конструкций: стержни ферм, колонны, штоки паровых машин и поршневых насосов, стяжные винты, канаты лебедок и другие детали.
Сдвиг или срез возникает, когда внешние силы смещают два параллельных сечения одно относительно другого, при неизменном расстоянии между ними. На сдвиг или срез работают, например, заклепки или болты, скрепляющие элементы, которые внешние силы пытаются сдвинуть (рис. 3).
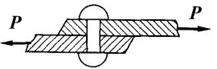
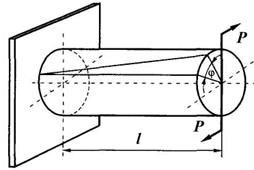
Рис. 3 Рис. 4
Кручение возникает при действии на стержень внешних сил, образующих моменты относительно продольной оси стержня. При этом из шести внутренних сил только 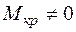 . На кручение работают валы, шпиндели токарных и сверлильных станков, роторы двигателей и другие детали (рис. 4).
. На кручение работают валы, шпиндели токарных и сверлильных станков, роторы двигателей и другие детали (рис. 4).
Изгиб — это такой вид нагружения, когда внешние силы вызывают моменты относительно оси симметрии (или главной оси), расположенный в плоскости поперечного сечения. Этот момент называется изгибающим. Самый простой случай — это плоский изгиб, когда все внешние силы лежат в одной плоскости, совпадающей во всех рассматриваемых нами случаях с плоскостью симметрии (или главной плоскостью) балки.
Метод сечений.Чтобы правильно рассчитать конструкцию на прочность или на жесткость, необходимо уметь определять внутренние силы по нагрузке. Для выявления внутренних сил в сопротивлении материалов применяется метод сечений, суть которого заключается в следующем.

 Для установления связи между внешними и внутренними силами используется метод сечений. Так как внутренние силы взаимно уравновешены и стоит задача выразить их через внешние, то необходимо выполнить такую операцию со стержнем, чтобы внутренние силы стали явными. Прием мысленного рассечения стержня на две части плоскостью, перпендикулярной продольной оси (рис. 1.10, а и б),и отбрасывания одной из полученных частей (рис. 1.10, в), позволяет перевести внутренние силы (рис. 1.10, в и г),для целого стержня уравновешенные, во внешние для оставленной части стержня. Эти силы взаимодействия есть в каждой точке проведенного сечения и они заменяют действие отброшенной части на оставшуюся. Эту систему большого числа сил (рис. 1.10, б) по правилам теоретической механики можно привести к одной точке (центру тяжести поперечного сечения), в результате чего получим главный вектор
Для установления связи между внешними и внутренними силами используется метод сечений. Так как внутренние силы взаимно уравновешены и стоит задача выразить их через внешние, то необходимо выполнить такую операцию со стержнем, чтобы внутренние силы стали явными. Прием мысленного рассечения стержня на две части плоскостью, перпендикулярной продольной оси (рис. 1.10, а и б),и отбрасывания одной из полученных частей (рис. 1.10, в), позволяет перевести внутренние силы (рис. 1.10, в и г),для целого стержня уравновешенные, во внешние для оставленной части стержня. Эти силы взаимодействия есть в каждой точке проведенного сечения и они заменяют действие отброшенной части на оставшуюся. Эту систему большого числа сил (рис. 1.10, б) по правилам теоретической механики можно привести к одной точке (центру тяжести поперечного сечения), в результате чего получим главный вектор 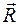 и главный момент
и главный момент 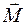 (рис. 1.10, в).
(рис. 1.10, в).
Теперь спроецируем 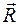 и
и 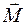 (рис. 1.10, г)на три оси (продольную z и две взаимно перпендикулярные поперечные x, y). В результате получим шесть внутренних силовых факторов: три силы
(рис. 1.10, г)на три оси (продольную z и две взаимно перпендикулярные поперечные x, y). В результате получим шесть внутренних силовых факторов: три силы 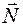 ,
, 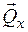 и
и 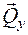 и три момента
и три момента 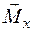 ,
, 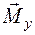 ,
, 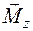 . Сила
. Сила 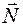 называется продольной силой, силы
называется продольной силой, силы 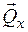 и
и 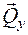 — поперечные силы. Момент относительно оси z —
— поперечные силы. Момент относительно оси z — 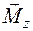 — крутящий момент (обычно обозначается как
— крутящий момент (обычно обозначается как 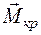 ); моменты
); моменты 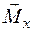 ,
, 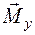 относительно поперечных осей — изгибающие. Каждому из внутренних усилий соответствует определенный вид деформации (изменение формы) бруса. Например, продольной силе
относительно поперечных осей — изгибающие. Каждому из внутренних усилий соответствует определенный вид деформации (изменение формы) бруса. Например, продольной силе 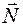 соответствует растяжение (или сжатие) бруса. Таким образом, рассматривается одна из полученных при рассечении части стержня, которая нагружена приложенными к этой часть внешними силами и шестью внутренними усилиями.
соответствует растяжение (или сжатие) бруса. Таким образом, рассматривается одна из полученных при рассечении части стержня, которая нагружена приложенными к этой часть внешними силами и шестью внутренними усилиями.
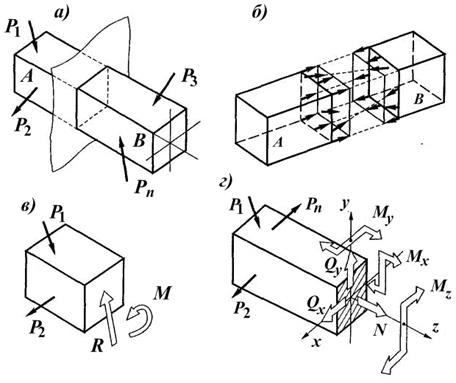
Рис. 1.10
Для установления связи внутренних и внешних сил можно к этой части применить уравнения равновесия (уравновешиваем), так как известно, что если тело находится в целом в равновесии, то в равновесии и любая его часть. Для пространственной системы существует 6 уравнений равновесия:
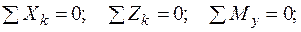
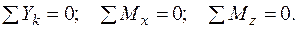
Рассмотрим, например, уравнение 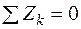 . Из внутренних усилий (рис. 8) на ось z проектируется только продольная сила
. Из внутренних усилий (рис. 8) на ось z проектируется только продольная сила 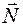 . Тогда
. Тогда
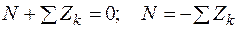 ,
,
где 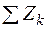 — сумма проекций всех внешних сил, действующих на оставленную часть стержня, на ось z. Отсюда вытекает следующее определение: продольная сила N численно равна алгебраической сумме проекций на ось стержня всех внешних сил, расположенных по одну сторону (рассматриваемую) от проведенного сечения (рис. 1.10, г).
— сумма проекций всех внешних сил, действующих на оставленную часть стержня, на ось z. Отсюда вытекает следующее определение: продольная сила N численно равна алгебраической сумме проекций на ось стержня всех внешних сил, расположенных по одну сторону (рассматриваемую) от проведенного сечения (рис. 1.10, г).
По первым буквам выполняемых операций (рассекаем, отбрасываем, заменяем и уравновешиваем) метод сечений иногда называют методом РОЗУ.
Эпюры внутренних силовых факторов и их особенности.Задача определения наибольших напряжений начинается с поиска сечения, в котором действуют наибольшие внутренние усилия. Как Вы думаете, где возникнет наибольший изгибающий момент в случае прямого поперечного изгиба консольной балки, нагруженной сосредоточенной силой 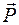 (рис.1.11, а)? Нетрудно догадаться, что опасным будет сечение Ау заделки, так как здесь действует максимальный изгибающий момент, равный
(рис.1.11, а)? Нетрудно догадаться, что опасным будет сечение Ау заделки, так как здесь действует максимальный изгибающий момент, равный 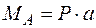 .
.
Опасное сечение— это поперечное сечение, в котором действуют наибольшие внутренние усилия.
А где будет располагаться опасное сечение в более сложном случае нагружения (рис. 1.11, б)? Сразу дать правильный ответ достаточно трудно, так как сосредоточенный изгибающий момент 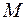 и распределенная нагрузка
и распределенная нагрузка 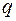 изгибают балку вниз, а сосредоточенная сила
изгибают балку вниз, а сосредоточенная сила 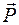 — вверх, при этом величины моментов от каждого вида нагрузки различны.
— вверх, при этом величины моментов от каждого вида нагрузки различны.
а) б)
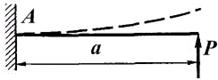
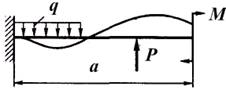
Рис. 1.11
Поэтому для сложных случаев нагружения необходимо знать закон изменения по длине балки изгибающего момента или другого внутреннего усилия (например, продольной силы 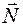 , поперечной силы
, поперечной силы 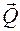 или крутящего момента
или крутящего момента 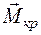 ). Этот закон можно изобразить с помощью специальных графиков, называемых эпюрами.
). Этот закон можно изобразить с помощью специальных графиков, называемых эпюрами.
В случаях растяжения — сжатия (рис. 1.12, а) или кручения (рис. 1.12, б) ординаты эпюр продольных сил или крутящих моментов также показывают их величины в соответствующих поперечных сечениях.
Любое внутреннее усилие определяется по внешним нагрузкам при помощи метода сечений. Каждая эпюра на разных участках имеет различные знаки.
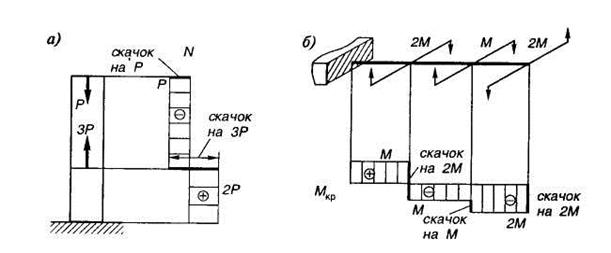
Рис. 1.12
Правила знаков внутренних силовых факторов (ВСФ).Рассмотрим правила знаков для внутренних усилий, применяемые в машиностроении:
1. Продольная сила 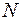 считается положительной, если она вызывает растяжение отсеченной части и отрицательной, если вызывает ее сжатие.
считается положительной, если она вызывает растяжение отсеченной части и отрицательной, если вызывает ее сжатие.
2. Поперечная сила 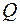 считается положительной, если она вращает отсеченную часть по ходу часовой стрелки и отрицательной, если вращение происходит против хода часовой стрелки.
считается положительной, если она вращает отсеченную часть по ходу часовой стрелки и отрицательной, если вращение происходит против хода часовой стрелки.
3. Изгибающий момент положителен, если сжаты верхние волокна отсеченной части, и отрицателен, если сжаты нижние волокна. Эпюра изгибающих моментов строится на сжатых волокнах.
4. Правило знаков для крутящего момента удобно принимать произвольным.
Запишем выражение изгибающих моментов для текущегосечения z, например, в консольной балке, находящейся под действиемсосредоточенной силы (рис. 1.12):
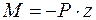 — уравнение прямой.
— уравнение прямой.
Из этого следует, что на прямолинейном ненагруженном внешней пролетной нагрузкой участке стержня эпюра моментов 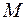 прямолинейна, а эпюра поперечных сил
прямолинейна, а эпюра поперечных сил 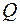 постоянна (рис. 1.13, а, б, в).
постоянна (рис. 1.13, а, б, в).
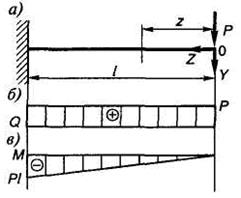
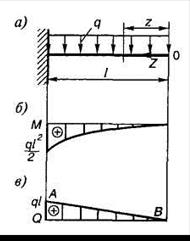
Рис. 1.13 Рис. 1.14
Запишем выражение изгибающих моментов для текущего сечения z в случае изгиба консольной балки, находящейся под действием равномерно распределенной нагрузки (рис. 1.14, а):
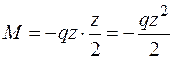
— это уравнение квадратной параболы.
В соответствии с дифференциальной зависимостью Журавского:
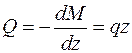 — уравнение прямой.
— уравнение прямой.
Таким образом, на участке с распределенной нагрузкой эпюры изгибающих моментов 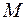 очерчены по квадратичной параболе с выпуклостью навстречу действию распределенной нагрузки, а эпюра поперечных сил
очерчены по квадратичной параболе с выпуклостью навстречу действию распределенной нагрузки, а эпюра поперечных сил 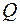 имеет вид трапеции или треугольника и ограничена прямой наклонной линией АВ, при этом направление наклона (при обходе слева направо) совпадает с направлением
имеет вид трапеции или треугольника и ограничена прямой наклонной линией АВ, при этом направление наклона (при обходе слева направо) совпадает с направлением 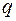 (рис. 1.13 и 1.14).
(рис. 1.13 и 1.14).
Примеры построения эпюр (рис. 1.15).
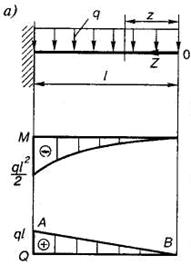
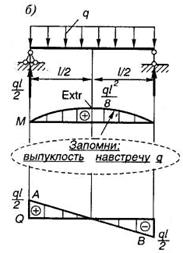
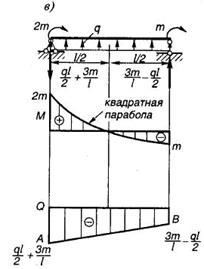
Рис. 1.15
