Матрицаларға қолданылатын амалдар
1. Бірдей өлшемді матрицаларды қосуға (алуға) болады, ол үшін олардың сәйкес элементтерін қосады (алады). 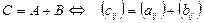
Матрицаларды қосуда нақты сандарға орындалатын ауыстырымдылық пен терімділік қасиеттер орындалады:
а) 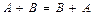 ; б)
; б) 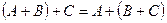 ; в)
; в) 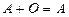 ; г)
; г) 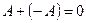 .
.
2. Матрицаны санға немесе санды матрицаға көбейту үшін оның барлық элементтерін сол санға көбейтеміз: 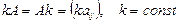 .
.
Бұл амалда мына қасиеттер орындалады:
а) 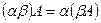 (сандар көбейткіштеріне терімділік қасиет);
(сандар көбейткіштеріне терімділік қасиет);
б) 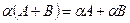 (матрицалардың қосындысына үлестірімділік қасиет);
(матрицалардың қосындысына үлестірімділік қасиет);
в) 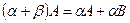 (сандардың қосындысына үлестірімділік қасиет);
(сандардың қосындысына үлестірімділік қасиет);
3. Матрицаны матрицаға көбейту үшін бірінші көбейткіш матрицаның тік жолдарының саны екінші көбейткіш матрицаның жатық жолдарының санына тең болуы керек, яғни 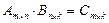 . Нәтижеде шыққан С матрицасының жатық жолының саны бірінші матрицамен, тік жолының саны екінші матрицамен бірдей болады. Ал оның кез келген элементі мына формуламен анықталады:
. Нәтижеде шыққан С матрицасының жатық жолының саны бірінші матрицамен, тік жолының саны екінші матрицамен бірдей болады. Ал оның кез келген элементі мына формуламен анықталады:
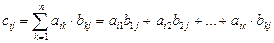 ,
, 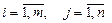 .
.
Көбейтуде мына қасиеттер орындалады: а) 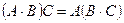 (терімділік қасиет);
(терімділік қасиет);
б) 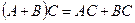 (үлестірімділік қасиет). Жалпы жағдайда, ауыстырымдылық қасиет орындалмайды:
(үлестірімділік қасиет). Жалпы жағдайда, ауыстырымдылық қасиет орындалмайды: 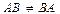 . Ал, егер
. Ал, егер 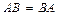 орындалса, ондай матрицалар ауыстырымды деп аталады; в)
орындалса, ондай матрицалар ауыстырымды деп аталады; в) 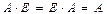 ;
;
Матрицаның барлық жатық жолдарын оның сәйкес тік жолдарымен орын алмастыру оны транспонирлеу (кері көшіру) деп аталады.
Қасиеттері: 1. 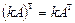 ,
, 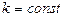 ; 2.
; 2. 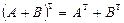 ; 3.
; 3. 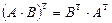 ;
;
4. 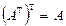 ; 5.
; 5. 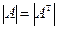 ; 6.
; 6. 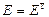 .
.
Анықтама. 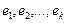 жолдарының сызықты комбинациясы деп
жолдарының сызықты комбинациясы деп 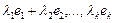 , (
, ( 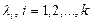 - сандар) қосындысын айтады.
- сандар) қосындысын айтады.
Егер матрицаның бір жолының элементтері басқа параллель жолдарының элементтерінің сызықты комбинациясы болса, онда оның жолдары сызықты тәуелді деп аталады.
Сызықты тәуелділікті анықтау үшін мынандай элементар түрлендірулер қолданылады:
1) кез келген жол элементтерін 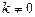 санына көбейту;
санына көбейту;
2) екі параллель жолдарын алмастыру;
3) кез келген жол элементтерін 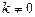 санына көбейтіп оған параллель кез келген жолдың сәйкес элементтеріне қосу.
санына көбейтіп оған параллель кез келген жолдың сәйкес элементтеріне қосу.
4) нөлдік жолды алып тастау.
Егер біреуі екіншісінен элементар түрлендірулер арқылы алынса, онда екі матрица эквивалентті деп аталады, яғни 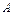 ~В.
~В.
Анықтауыштар.Әрбір квадрат матрица үшін белгілі бір ереже бойынша туындаған сан осы матрицаның анықтауышы болады.
Анықтама. Екінші ретті анықтауыш деп 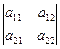
 сандар кестесіне сәйкес келетін
сандар кестесіне сәйкес келетін 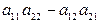 айырымын айтамыз.
айырымын айтамыз.
Анықтама. Үшінші ретті анықтауыш деп 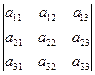 сандар кестесіне сәйкес келетін мына санды айтамыз:
сандар кестесіне сәйкес келетін мына санды айтамыз: 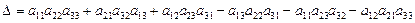 .
.
Бұл ережені үшінші ретті анықтауышты есептеудің Саррюс немесе үшбұрыштар ережесі деп атайды.
Анықтама. 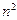 элементтен тұратын квадрат кестесіне сәйкес
элементтен тұратын квадрат кестесіне сәйкес 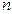 - ретті анықтауыш деп жіктелу туралы және басқа да қасиеттерді пайдалана отырып алынған санды айтады, оны мына cимволмен белгілейді:
- ретті анықтауыш деп жіктелу туралы және басқа да қасиеттерді пайдалана отырып алынған санды айтады, оны мына cимволмен белгілейді: 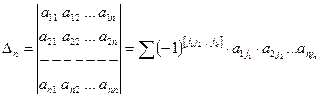 .
.
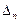 - анықтауыштың
- анықтауыштың 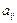 - элементінің миноры деп, осы анықтауыштың
- элементінің миноры деп, осы анықтауыштың 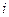 - жатық,
- жатық, 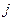 - тік жолдарынсыз алынған
- тік жолдарынсыз алынған 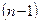 - ретті анықтауышты айтамыз және оны
- ретті анықтауышты айтамыз және оны 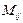 әрпімен белгілейміз.
әрпімен белгілейміз.
Анықтама. Анықтауыштың 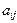 элементінің алгебралық толықтауышы деп «+» немесе «-» таңбасымен алынған осы элементтің минорын айтамыз, ол
элементінің алгебралық толықтауышы деп «+» немесе «-» таңбасымен алынған осы элементтің минорын айтамыз, ол 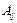 әрпімен белгіленеді, яғни
әрпімен белгіленеді, яғни 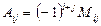 ,
, 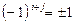
Мысал. 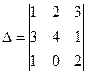
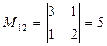 ,
, 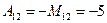
Квадрат матрицалар үшін мына теңдік орындалады: 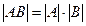
Анықтауышты анықтамасы бойынша есептейді. Және анықтауышты үшбұрышты түрге келтіріп те есептейді. Егер анықтауыштың бас диагоналінің астындағы немесе үстіндегі барлық элементтері нөлге тең, яғни 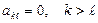 немесе
немесе 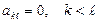 болса, онда ол бас диагональ элементтерінің көбейтіндісіне тең:
болса, онда ол бас диагональ элементтерінің көбейтіндісіне тең: 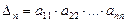 . Мысалы:
. Мысалы: 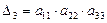 .
.
Егер бүйір (қосалқы) диагональ үстіндегі немесе астындағы барлық элементтер нөлге тең болса, онда 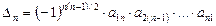 . Мысалы:
. Мысалы: 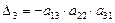 .
.
