Частотные характеристики параллельного колебательного контура

Для простоты рассмотрим идеальный контур, то есть контур без активных сопротивлений в ветвях (рис.2.26):

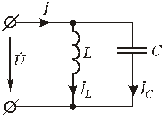
Рис.2.26. Параллельный колебательный контур

На рис.2.27 построены частотные характеристики реактивных проводимостей b_L и b_C, а также суммарной проводимости цепи b = = b_L + b_C.

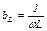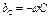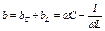; ; . 62(2.52)

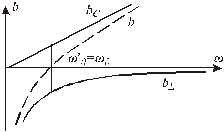
Рис.2.27. Частотные характеристики параллельного
колебательного контура

Ток в неразветвленной части цепи:

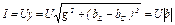. 63(2.53)

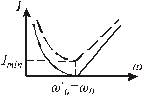
Рис.2.28. График зависимости тока в
неразветвленной части цепи от частоты

Полученный график говорит о том, что в момент резонанса об­щий ток, потребляемый цепью, равен нулю, несмотря на наличие токов в ветвях, что в свою очередь подтверждается векторной диаграммой (рис.2.29).

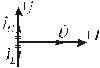
Рис.2.29. Векторная диаграмма для резонансного режима
идеального параллельного контура

При учете сколь угодно малого активного сопротивления цепи ток при резонансе не равен нулю. Пунктирная кривая изображает реальный ток в цепи.

Мощности

Рассчитаем мощность произвольного приемника, представленного на рисунке рис.2.30 в виде пассивного двухполюсника.

Рис.2.30. Пассивный двухполюсник

Пусть u = U_msinwt – подводимое напряжение; φ_u – φ_I = j.

При φ_u=0 имеем i = I_msin(wt – j).

Тогда:

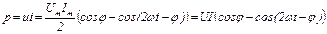.64(2.54)

Построим график полученной функции p(wt):

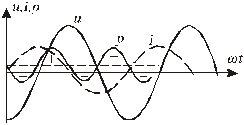
Рис.2.31. Зависимость мгновенных значений тока,
напряжения и мощности произвольного
двухполюсника в функции фазы ωt

Полученный график говорит о том, что функция мгновенной мощности знакоперемен­на. Это значит, что двухполюсник имеет активно-реактивный характер. Если бы двухполюсник не содержал реактивных элементов, то график полностью бы лежал над осью wt. Найдем среднее значение мгновенной мощности:

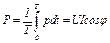. 65(2.55)

Эта мощность называется активной мощностью. Единица измерения активной мощности – [Вт].

Наряду с активной вводится понятие полной мощности:

S = UI. 66(2.56)

Единица измерения полной мощности – [В×А].

P/S = cosj – коэффициент мощности.

Разность полной и активной мощности, обусловленная наличием реактивных (индуктивных и емкостных) элементов называется реактивной мощностью:

Q = Q_L – Q_C = UIsinj 67(2.57)

Единица измерения реактивной мощности – [вар]. Мощности связаны между собой соотношением:

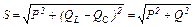68(2.58)

Треугольник мощностей (2.32.a) можно получить из векторной диаграммы напряжений (рис.2.14), умножив стороны прямоугольного треугольника на вектор :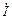

В этом треугольнике:

сторона ab – P = U_RI = I²R = UIcosj;

сторона bc – Q = Q_L – Q_C = (U_L – U_C)I = I²(X_L – X_C) = UIsinj;

сторона ac – .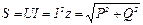

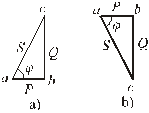
Рис.2.32. Треугольники мощностей на основе
векторной диаграммы напряжений (а)
и векторной диаграммы токов (b)

Аналогичный треугольник мощностей можно получить из векторной диаграммы токов, умножив все стороны треугольника токов на вектор 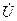. В этом треугольнике (2.32.b):

cторона ab – P = I_RU = I²g = UIcosj;

сторона bc – Q = Q_L – Q_C = (I_L – I_C)U = U²b = UIsinj;

сторона ac – 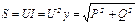;