Z – түрлендірудің негізгі түсініктемелері

x(t) үздіксіз уақыт функциясы төмендегі белгілі формула бойынша Лапластың бейнесімен алмастырылуы мүмкін. 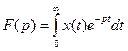(9.9)

Егер Т реттеу аралығына тең дискретті уақыт аралығын алсақ, және үздіксіз уақытты мына түрде көрсетсек t = 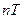, мұндағы 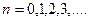импульстік реттік номері, онда (9.9) өрнегіндегі интегралды мына суммамен алмастыруға блады. 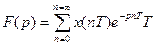(9.l0)

Немесе 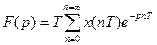(9.ll)

Мынадай белгілеу енгіземіз 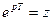(9.l2)

және оны (9.ll) өрнегін қойып шығамыз 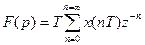(9.l3)

Өрнек 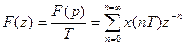(9.l4)

дискреттік уақыт функциясының 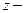түрлендіруі деп аталады.

Кейде символдық түрінде жазылады.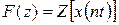

Қарапайым Лаплас түрлендіруіндегі операторы комплекстік санды береді .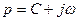

Жиіліктік сипаттамаға өткен кезде 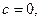операторының нақты бөлігі мен 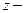түрлендірудің операторы бұл жағдайда. 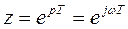(9.l5)

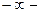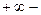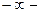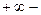Егер аргументі тен ке дейін өзгеретін болса, онда операторы тен ке дейінгі сәйкес комплекстік жазықтықтың жорамал өсін жағалай өзгереді, ал бұл кезде 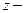оперторы бірлік радистың шеңбері бойынша өзгерді.

Осылай (9.l5) түрлендіруі комплекстік жазықтықтың жорамал өсін жазықтыңындағы бірлік радустың жазықтығына бейлелейді. Осы кезде комплекстік жазықтығының сол жақ жартылай жазықтығы С жазықтығындағы бірлік радусты шеңберіне бейнеленеді.

Көп мөлшердегі функция үшін түрлендіру кестесі құрылған. 9.l.кестеде бірнеше функцияның түрленуі келтірілген.Толық кестелер [23]-те берілген.

түрлендіруден уақыт функциясына айналу формуласы бойынша кері өтеді

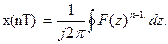(9.l6)

Интегралдаушы 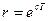шеңбер радусы бойынша жүргізіледі. Кері өтуді түрлендіруден дәрежелері бойынша Лоран қатарына бөлу арқылыорындау оңай. Көптеген нақты жүйелер үшін түрленендіру бөлшекті – рационалды функцияны береді, оны Лоран қатарына жайғана бөлімін алына бөлу арқылы бөлуге болады.

Сәйкес дәрежелердгі коэффициенттер дискретті момент уақытының мәндеріне тең 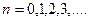және т.б.

9.l – кесте

Оригинал	Қарапайым түрлендіру	Модифицирленген түрлендіру
1(t)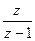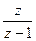
t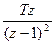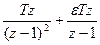
e-at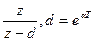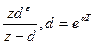
1-e-at		-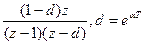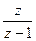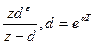
sin bt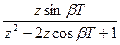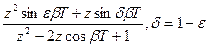
cos bt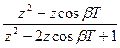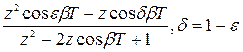

Мысал. Функцияның оригиналын табайық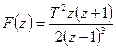

Бөлімін алымына бөлсек шексіз қатар аламыз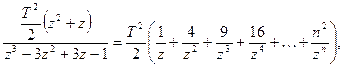

Осыдан 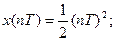мұндағы 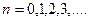және т.б.

(9.l0) өрнегін ескере отырып, аламыз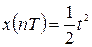

Сонымен қатар кешігуші түрлендіру де кеңінен қолданылады

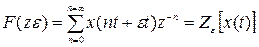(9.l7)

Мұнда 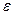коэффициенті 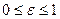аралығындағы мәндерді қабылдауы мүмкін. (9.l7) өрнегінен кешігуші түрлендіру үздіксіз функция үшін дискретті 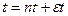уақыт моментінде анықталатыны шығады. Бұл уақыт моменттері негізгі дискретті уақыт моментіне қатынасы бойынша 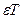шамаға озып кету жағына қарай жылжытылған сондықтан кейде бұл түрлендіруді «упреждающий» түрлендіру деп, немесе модифицирленген түрлендіру деп атайды. Мұндай түрлендіру шығыс шамасын реттеу аралығының ішіндегі кез – келген уақыт моментінде есептеуге мүмкіндік береді.

9.l.кестеде сонымен қатар кешігуші түрлендіру мәндері де келтірілген түрлендіру теориясында негізінде қарапайым Лаплас түрлендіру теоремасына ұқсас теоремалар бар. Бұл теоремалардың дәлелдемелері (2l,23) - те келтірілген.

Негізгі әдебиет: 1 [323-385].

Қосымша әдебиет: 1 [336-364]

Бақылау сұрақтар:

1. Қандай жүйелер сызықты импульстік реттеу жүйелер деп аталады?
2. Сызықты импульсті реттеу жүйеснің қандай ерекшеліктері бар және қандай жағдайларда қолданылады?
3. Импульстік үзбелердің қандай типтері қолданылады?
4. Импульстік жүйелерді зерттеу үшін қандай математикалық әдістер пайдаланылады?
5. ­-түрлендірудің мәні неде?
6. Тура және кері -түрлендіруді қалай алуға болады?
7. Ажыратылған, тұйықталған, ауытқу бойынша (қатемен) импульстік жүйенің дискретті беріліс функциясын қалай аламыз?
8. Импульсті жүйе тұрақтылығын қалай зерттеуге болады?
9. Импульстік жүйе сапасын қалай зерттейміз?

№ 13 Дәрістің конспектісі:

Дәрістің тақырыбы: Негізгі әсері бойынша басқару жүйелері, комбинирленген жүйелер (қиыстырылған). Осы жүйелердегі компенсаторлар реттегішін синтездеу.