Обнаружение и исправление ошибок

Общие понятия

Для защиты полезной информации от помех необходимо в том или ином виде вводить избыточность: увеличивать число символов и время их передачи, повторять целые сообщения, повышать мощность сигнала - все это ведет к усложнению и удорожанию аппаратуры. В качестве исследуемой модели достаточно рассмотреть канал связи с помехами, потому что к этому случаю легко сводятся остальные. Например, запись на диск можно рассматривать как передачу данных в канал, а чтение с диска – как прием данных из канала.

Коды без избыточности обнаружить, а тем более исправлять ошибки не могут. Количество символов, в которых любые две комбинации кода отличаются друг от друга, называется кодовым расстоянием.

Минимальное количество символов, в которых все комбинации кода отличаются друг от друга, называется минимальным кодовым расстоянием. Минимальное кодовое расстояние - параметр, определяющий помехоустойчивость кода и заложенную в коде избыточность, т.е. корректирующие свойства кода.

В общем случае для обнаружения t ошибок минимальное кодовое расстояние

d₀ = t + 1.

Минимальное кодовое расстояние, необходимое для одновременного обнаружения t и исправления s ошибок,

d₀ = t + s + 1.,

Для кодов, только исправляющих s ошибок,

d₀ = 2s + 1.

Для того чтобы определить кодовое расстояние между двумя комбинациями двоичного кода, достаточно просуммировать эти комбинации по модулю 2 и подсчитать число единиц полученной комбинации.

Для обнаружения и исправления одиночной ошибки соотношение между числом информационных разрядив k и числом корректирующих разрядов r должно удовлетворять следующим условиям:

,

,

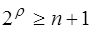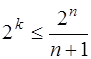при этом подразумевается, что общая длина кодовой комбинации

n = k + ρ

Для практических расчетов при определении числа контрольных разрядов кодов с минимальным кодовым расстоянием d₀ = 3 удобно пользоваться выражениями

ρ₁₍₂₎ = [ log₂ ( n + 1 ) ],

если известна длина полной кодовой комбинации n, и

ρ ₁₍₂₎ = [log₂ { ( k + 1 ) + [ log₂ ( k + 1) ] } ],

если при расчетах удобнее исходить из заданного числа информационных символов k .

Для кодов, обнаруживающих все трехкратные ошибки (d₀ = 4),

ρ ₁₍₃₎ ³ 1 + log₂ ( n + 1 ),

или

ρ ₁₍₃₎ ³ 1 + log₂ [ ( k + 1 ) + log₂ ( k + 1 ) ].

Для кодов длиной в n символов, исправляющих одну или две ошибки (d₀ = 5),

ρ ₂ ³ log₂ (C_n² + C_n¹ + 1).

Для практических расчетов можно пользоваться выражением:

.

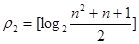Для кодов, исправляющих 3 ошибки (d₀ = 7),

.

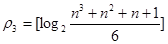Линейные групповые коды

Линейными называются коды, в которых проверочные символы представляют собой линейные комбинации информационных символов.

Для двоичных кодов в качестве линейной операции используется сложение по модулю 2.

Последовательность нулей и единиц, принадлежащих данному коду, будем называть кодовым вектором.

Свойство линейных кодов:

сумма (разность) кодовых векторов линейного кода дает вектор, принадлежащий данному коду.

Линейные коды образуют алгебраическую группу по отношению к операции сложения по модулю 2. В этом смысле они являются групповыми кодами.

Свойство группового кода:

минимальное кодовое расстояние между кодовыми векторами группового кода равно минимальному весу ненулевых кодовых векторов.

Вес кодового вектора (кодовой комбинации) равен числу его ненулевых компонент.

Расстояние между двумя кодовыми векторами равно весу вектора, полученного в результате сложения исходных векторов по модулю 2. Таким образом, для данного группового кода

W_min =d_0.

Групповые коды удобно задавать матрицами, размерность которых определяется параметрами кода k и r. Число строк матрицы равно k, число столбцов равно

n = k + r :

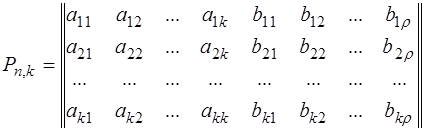
Коды, порождаемые этими матрицами, известны как (n,k)-коды, соответствующие им матрицы называют порождающими (производящими, образующими).

Порождающая матрица P может быть представлена двумя матрицами U_k и H_r (информационной и проверочной). Число столбцов матрицы H_r равно r, число столбцов матрицы U_k равно k

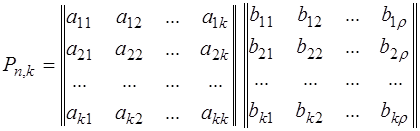
Теорией и практикой установлено, что в качестве матрицы U_k удобно брать единичную матрицу в канонической форме

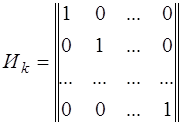
Для кодов с d_0­ = 2 производящая матрица P имеет вид

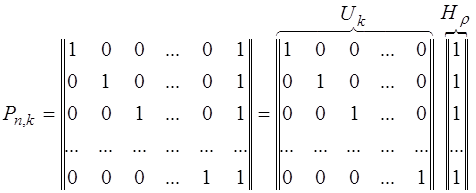
Во всех комбинациях кода построенного при помощи такой матрицы, четное число единиц.

Для кодов с d₀ ³ 3 порождающая матрица не может быть представлена в форме, общей для всех кодов с данным d_0­. Вид матрицы зависит от конкретных требований к порождающему коду. Этими требованиями могут быть либо минимум корректирующих разрядов, либо максимальная простота аппаратуры.

Корректирующие коды с минимальным количеством избыточных разрядов называют плотно упакованнымиили совершенными кодами.

Для кодов d₀ = 3 соотношения n и k следующие: (3; 1), (7; 4),
(15; 11), (31; 26), (63; 57) и так далее.

Строчки образующей матрицы P представляют собой k комбинаций искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы по следующему правилу: корректирующие символы, предназначенные для обнаружения и исправления ошибки в информационной части кода, находятся путем суммирования по модулю 2 тех строк матрицы H_r, номера которых совпадают с номерами разрядов, содержащих единицы в кодовом векторе, представляющем информационную часть кода. Полученную комбинацию приписывают справа к информационной части кода и получают полный вектор корректирующего кода. Аналогичную процедуру проделывают со второй, третьей и последующими информационными кодовыми комбинациями, пока не будет построен корректирующий код для передачи всех символов первичного алфавита.

Алгоритм образования проверочных символов по известной информационной части кода может быть записан следующим образом

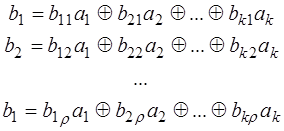
или

.

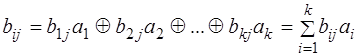В процессе декодирования осуществляются проверки, идея которых в общем виде может быть представлена следующим образом

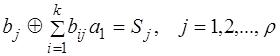
Для каждой конкретной матрицы существует своя, одна-единственная система проверок. Проверки производятся по следующему правилу : в первую проверку вместе с проверочным рядом b₁ входят информационные разряды, которые соответствуют единицам первого столбца проверочной матрицы H_r; во вторую проверку входит второй проверочный разряд b₂ и информационные разряды, и т. д. Число проверок равно числу проверочных разрядов корректирующего кода r.

В результате осуществления проверок образуется проверочный вектор S₁, S₂, ..., S_r, который называется синдромом. Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, то принятая комбинация содержит ошибку. Исправление ошибки производится по виду синдрома, так как каждому ошибочному разряду соответствует один единственный проверочный вектор.

Вид синдрома для каждой конкретной матрицы может быть определен при помощи проверочной матрицы Н’, которая представляет собой транспонированную матрицу H_r, дополненной единичной матрицей I_r, число столбцов которой равно число проверочных разрядов кода

Н’ = úçH_r^ТI_rúç.

Столбцы такой матрицы представляют собой значение синдрома для разряда, соответствующего номеру столбца матрицы Н’.

Процедура исправления ошибок в процессе декодирования групповых кодов сводится к следующему.

Строится кодовая таблица. В первой строке таблицы располагаются все кодовые векторы A_i. В первом столбце второй строки размещается вектор a₁, вес которого равен 1.

Остальные позиции второй строки заполняются векторами, полученными в результате суммирования по модулю 2 вектора a₁ с А_i, расположенным в соответствующем столбце первой строки. В первом столбце третьей строки записывается вектор a₂, вес которого также равен 1, однако , если вектор a₁ содержит единицу в первом разряде, то a₂ - во втором. В остальные позиции третьей строки записывают суммы А_i и a₂ .

Аналогично поступают до тех пор, пока не будут просуммированы с векторами А_i все векторы a_j весом 1, с единицей в каждом из n разрядов. Затем суммируются по модулю 2 векторы a_j, весом 2, с последовательным перекрытием всех возможных разрядов. Вес вектора a_j определяет число исправляемых ошибок. Число векторов a_j определяется возможным числом неповторяющихся синдромов и равно 2^r-1 (нулевая комбинация говорит об отсутствии ошибки). Условие неповторяемости синдрома позволяет по его виду определять один-единственный соответствующий ему вектор a_j. Векторы a_j есть векторы ошибок, которые могут быть исправлены данным групповым кодом.

По виду синдрома принятая комбинация может быть отнесена к тому или иному смежному классу, образованному сложением по модулю 2 кодовой комбинации А_i с вектором ошибки a_j, т. е. к определенной строке кодовой таблицы 3.2.1.

Таблица 3.2.1- Кодовая таблица групповых кодов

a	A1	A2	...	A(2k-1)
a1	a1ÅA1	a2ÅA2	...	a1ÅA(2k-1)
a2	a2ÅA1	a2ÅA2	...	a2ÅA(2k-1)
...	...	...	...	...
a(2r-1)	a­(2 r- 1)ÅA1	a(2r­-1)­ÅA2	...	a(2r-1)ÅA(2k-1)

Принятая кодовая комбинация A^x_n сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в строке той же колонки таблицы. Процесс исправления ошибки заключается в замене на обратное значение разрядов.

Векторы a₁, a₂, ...,a₍₂^r_-1) не должны быть равными ни одному из векторов А₁, А₂, ..., А₍₂^r_-1), в противном случае в таблице появились бы нулевые векторы.

Пример.

Построить кодовую таблицу, при помощи которой обнаруживаются и исправляются все одиночные ошибки и некоторые ошибки кратностью r + 1, в информационной части кода (11,7), построенного по матрице

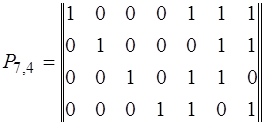
Решение.

Используя таблицу 3.2.1, строим кодовую таблицу 3.2.2 для кодов, построенных по данной матрице P, кодовые комбинации строятся путем добавления к четырехразрядным комбинациям натурального двоичного кода корректирующих разрядов по правилу, описанному выше.

Определяем систему проверок исходя из матрицы H_r

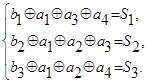
Находим вид синдрома для каждой строки таблицы. Для этого достаточно произвести проверки для кодовых комбинаций любого столбца кодовой таблицы.

Для нашего примера возьмем столбец A₃ .

Таблица 3.2.1 – Пример таблицы для столбца А₃

№	e	A1	A2	A3	A4	A5	A6	A7
№	A8	A9	A10	A11	A12	A13	A14	A15

1) 0 1 0 0 1 0 0

2) 1 0 0 0 1 0 0

3) 1 1 1 0 1 0 0

4) 1 1 0 1 1 0 0

5) 0 0 0 0 1 0 0

6) 0 1 0 1 1 0 0

7) 0 1 1 0 1 0 0

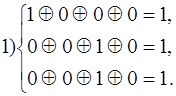
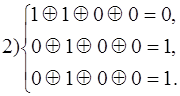
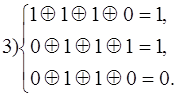
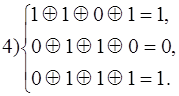
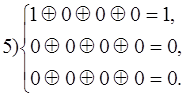
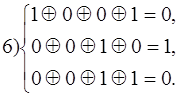
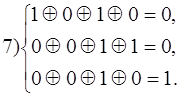
Таким образом вектору ошибки a₁ соответствует синдром 1 1 1

__________ “____________ a₂________ “_________ 0 1 1

__________ “____________ a₃________ “_________ 1 1 0

__________ “____________ a₄________ “_________ 1 0 1

__________ “____________ a₅________ “_________ 1 0 0

__________ “____________ a₆________ “_________ 0 1 0

__________ “____________ a₇________ “_________ 0 0 1

Предположим, приняты комбинации 1011001, 1000101, 0001100, 0000001 и 1010001. Производим проверки

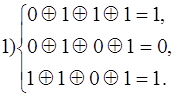
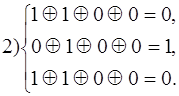
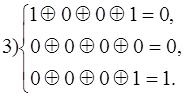
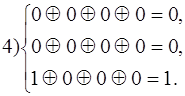
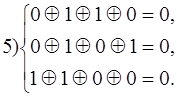
Синдром первой принятой комбинации - 101, значит вектор ошибки а₄ = 0001000, исправление ошибки производится заменой символа в четвертом разряде принятой комбинации на обратный. Истинная комбинация - А₅, так как принятая комбинация находится в шестом столбце таблицы в строке, соответствующей синдрому 101.

Синдром второй принятой комбинации - 010, находим ее в шестой строке (010 соответствует а₆) и в девятом столбце. Истинная комбинация А₈ = 0001101, т.е. исправлена двойная ошибка.

Синдром третьей принятой комбинации - 001 соответствует а₇, истинная комбинация А₁₃.

Синдром четвертой из принятых комбинаций - 001 также соответствует а₇, но принятую комбинацию мы находим в шестом столбце таблицы , следовательно, истинная комбинация - А₅.

Синдром шестой принятой комбинации - 000. Ошибки нет.

Код Хэмминга

Систематические кодыпредставляют собой такие коды, в которых информационные и корректирующие разряды расположены по строго определенной системе и всегда занимают строго определенные места в кодовых комбинациях. Систематические коды являются равномерными, т.е. все комбинации кода с заданными корректирующими способностями имеют одинаковую длину. Групповые коды также являются систематическими, но не все систематические коды могут быть отнесены к групповым.

Код Хэммингаявляется типичным примером систематического кода. Однако при его построении к матрицам обычно не прибегают. Для вычисления основных параметров кода задается либо количество информационных символов, либо количество информационных комбинаций N = 2^k. При помощи формул

,

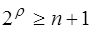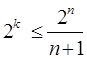
вычисляются k и r . Соотношения между n, k и r для кода Хэмминга представлены в таблице

Таблица 3.3.1 – Соотношения между n, k, r в коде Хэмминга

n	k	r	n	k	r

Зная основные параметры корректирующего кода, определяют: какие позиции кода будут информационными, а какие проверочными. Как показала практика, номера контрольных символов удобно выбирать по закону 2ⁱ, где i = 0, 1, 2 и т.д. - натуральный ряд чисел. Номера контрольных символов в этом случае будут соответственно: 1, 2, 4, 8, 16, 32 и т.д.

Затем определяют значения проверочных разрядов (0 или 1), руководствуясь следующим правилом: сумма единиц на проверочных позициях должна быть четной. Если эта сумма четна, то значение контрольного разряда - 0, в противном случае - 1.

Проверочные позиции выбираются следующим образом: составляется таблица для ряда натуральных чисел в двоичном коде. Число строк таблицы

n = k + r .

Первой строке соответствует проверочный символ a₁ второй - a₂ и т.д., как показано в таблице.

Таблица 3.3.2 – Ряд натуральных чисел в двоичном коде

n	Двоичный код	Провероч-ные коэффициенты	n	Двоичный Код	провероч-ные коэффициенты
	0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0	а1 a2 a3 a4 a5 a6		0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1	a7 a8 a9 a10 a11

Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу:

в первую проверку входят коэффициенты, которые содержат в младшем разряде 1, т.е. a₁, a₃,, a₅ , a₇ , a₉ ,a₁₁ и т.д.;

во вторую - коэффициенты, содержащие 1 во втором разряде, т.е. и т.д. a₂, a₃,, a₆ , a₇ , a₁₀ ,a₁₁ и т.д.;

в третью проверку - коэффициенты, которые содержат 1 в третьем разряде, и т.д.

Номера проверочных коэффициентов соответствуют номерам проверочных позиций, что позволяет составить общую таблицу проверок.

Таблица 3.3.3 – Таблица проверок

№ проверки	Проверочные позиции	№ провероч-ного разряда
	1, 3, 5, 7, 9, 11 ... 2, 3, 6, 7, 10, 11, 14, 15, 18,19, 22, 23, 26, 27, 30, 31 ... 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23, 28, 29, 30, 31 ... 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27, 28, 29, 30, 31, 40, 41, 42, 43, 44, 45, 46 ...

Старшинство разрядов считается слева направо, а при проверке сверху вниз. Порядок проверок показывает также порядок следования разрядов в полученном двоичном коде.

Если в принятом коде есть ошибка, то результаты проверок по контрольным позициям образуют двоичное число, указывающее номер ошибочной позиции. Исправляют ошибку, изменяя символ ошибочной позиции на противоположный.

Для исправления одиночной и обнаружения двойной ошибки, кроме проверок по контрольным позициям, следует проводить еще одну проверку на четность для каждого кода. Чтобы осуществить такую проверку, следует к каждому коду в конце кодовой комбинации добавить контрольный символ таким образом, чтобы сумма единиц в полученной комбинации была всегда четной. Тогда в случае одной ошибки проверки по позициям укажут номер ошибочной позиции, а проверка на четность укажет наличие ошибки. Если проверки позиций укажут на наличие ошибки, а проверка на четность не фиксирует ошибки, значит в коде две ошибки.

Пример.

Построить код Хэмминга для информационной комбинации 0101. Показать процесс обнаружения ошибки.

Решение.

Количество информационных разрядов k = 4. Находим значения общей длины кодовой комбинации и число контрольных символов: r = 3и n = 7. Так как общее количество символов кода n = 7, то контрольные коэффициенты займут три позиции: 1, 2 и 4.

Корректирующий код без значений контрольных коэффициентов будет иметь вид:

b₁ b₂ 0 b₃ 1 0 1.

Пользуясь таблицей проверочных позиций, определяем значения контрольных коэффициентов.

Первая проверка: сумма П₁ Å П₃ Å П₅ Å П₇ должна быть четной, а сумма b₁ Å 0 Å 1Å 1 будет четной при b₁ = 0.

Вторая проверка: сумма П₂ Å П₃ Å П₆ Å П₇ должна быть четной, а сумма b₂ Å 0 Å 0 Å 1 будет четной при b₂ = 1.

Третья проверка: сумма П₄ Å П₅ Å П₆ Å П₇ должна быть четной, а сумма b₃ Å 1Å 0 Å 1 будет четной при b₃ = 0.

Окончательно корректирующий код принимает вид:

0 1 0 0 1 0 1.

Предположим, в результате искажений в канале связи вместо 0100101 было принято 0100111. Для обнаружения ошибки производим контроль на четность, аналогичные проверкам при выборе контрольных коэффициентов.

Первая проверка: сумма П₁ Å П₃ Å П₅ Å П₇ = 0 Å 0 Å 1Å 1 четна. В младший разряд номера ошибочной позиции записываем 0.

Вторая проверка: сумма П₂ Å П₃ Å П₆ Å П₇ = 1 Å 0 Å 1Å 1 нечетна. Во второй разряд номера ошибочной позиции записываем 1.

Третья проверка: сумма П₄ Å П₅ Å П₆ Å П₇ = 0 Å 1 Å 1Å 1 нечетна. В третий разряд номера ошибочной позиции записываем 1.

Номер ошибочной позиции 110₂ = 6₁₀. Следовательно, символ шестой позиции следует изменить на обратный.

Циклические коды

Циклические коды названы так потому, что в них часть комбинаций кода либо все комбинации могут быть получены путем циклического сдвига одной или нескольких комбинаций кода. Циклический сдвиг осуществляется справа налево, причем крайний левый символ каждый раз переносится в конец комбинации. Циклические коды, практически, все относятся к систематическим кодам, в них контрольные и информационные разряды расположены на строго определенных местах. Кроме того, коды относятся к числу блочных кодов. Каждый блок (одна буква является частным случаем блока) кодируется самостоятельно.

Идея построения циклических кодов базируется на использовании неприводимых в поле двоичных чисел многочленов. Неприводимыми называются многочлены, которые не могут быть представлены в виде произведения многочленов низших степеней с коэффициентами из того же поля, так же, как простые числа не могут быть представлены произведением других чисел. Иными словами неприводимые многочлены делятся без остатка только на себя или на единицу.

Неприводимые многочлены в теории циклических кодов играет роль образующих многочленов. Если заданную кодовую комбинацию умножить на выбранный неприводимый многочлен, то получим циклический код, корректирующие способности которого определяются неприводимым многочленом.

Предположим, требуется закодировать одну из комбинаций четырехзначного двоичного кода. Предположим также, что эта комбинация G(x) = x³ + x² + 1 ® 1011. Пока не обосновывая свой выбор, берем из таблицы неприводимых многочленов в качестве образующего многочлен P(x) = x³ + x + 1 ® 1011. Затем умножим G(x) на одночлен той же степени, что и образующий многочлен. От умножения многочлена на одночлен степени n степень каждого члена многочлена повысится на n, что эквивалентно приписыванию n нулей со стороны младших разрядов многочлена. Так как степень выбранного неприводимого многочлена равна трем, то исходная информационная комбинация умножается на одночлен трех степеней

G(x) • xⁿ = (x³ + x² + 1) • x³=x⁶ + x⁵ + x³ = 1101000.

Это делается для того, чтобы впоследствии в месте этих нулей можно было бы записать корректирующие разряды.

Значение корректирующих разрядов находят по результатам от деления G(x) • xⁿ на P(x):

1 1 0 1 0 0 0 ½ 1 0 1 1 1 0 1 1 1 1 0 0 1 1 1 1 + 1 0 1 1 1 1 1 0 1 0 1 1 1 0 1 0 1 0 1 1 0 0 1

x⁶+x⁵+0+x³+0+0+0 ½x³+x+1

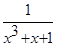x⁶+0+x⁴+x³

x⁵+x⁴+0+0 x³+x²+x+1+ x⁵+0+x³+x²

x⁴+ x³+x²+0

x⁴+ 0 +x²+x

x³+0+x+0

x³+0+x+1

Таким образом,

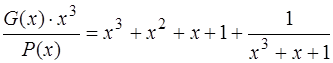
или в общем виде

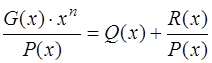(1)

где Q(x) ¾ частное, а R(x) ¾ остаток от деления G(x)×xⁿ на P(x).

Так как в двоичной арифметике 1 Å 1 = 0, а значит, -1 = 1, то можно при сложении двоичных чисел переносить слагаемые из одной части в другую без изменения знака (если это удобно), поэтому равенство вида a Å b = 0 можно записать и как a = b, и как a - b = 0. Все три равенства в данном случае означают, что либо a и b равны 0, либо a и b равны 1, т.е. имеют одинаковую четность.

Таким образом, выражение (1) можно записать как

F(x)=Q(x) • P(x)= G(x) • xⁿ+R(x),

что в случае нашего примера даст

F(x)=(x³ + x² + x + 1) • (x³ + x + 1)=(x³ + x² + 1) • x³ + 1,

или

F(x)=1111 • 1011 = 1101000 + 001 = 1101001.

Многочлен 1101001 и есть искомая комбинация, где 1101‑ информационная часть, а 001 ‑ контрольные символы. Заметим, что искомую комбинацию мы получили бы и как в результате умножения одной из комбинаций полного четырехзначного двоичного кода (в данном случае 1111) на образующий многочлен, так и умножением заданной комбинации на одночлен, имеющий ту же степень, что и выбранный образующий многочлен (в нашем случае таким образом была получена комбинация 1101000) с последующим добавлением к полученному произведению остатка от деления этого произведения на образующий многочлен (в нашем примере остаток имеет вид 001).

И тут решающую роль играют свойства образующего многочлена P(x). Методика построения циклического кода такова, что образующий многочлен принимает участие в образовании каждой кодовой комбинации, поэтому любой многочлен циклического кода делится на образующий без остатка. Но без остатка делятся только те многочлены, которые принадлежат данному коду, т. е. образующий многочлен позволяет выбрать разрешенные комбинации из всех возможных. Если же при делении циклического кода на образующий многочлен будет получен остаток, то значит либо в коде произошла ошибка, либо это комбинация какого-то другого кода (запрещенная комбинация). По остатку и обнаруживается наличие запрещенной комбинации, т. е. обнаруживается ошибка. Остатки от деления многочленов являются опознавателями ошибок циклических кодов.

С другой стороны, остатки от деления единицы с нулями на образующий многочлен используются для построения циклических кодов.

При делении единицы с нулями на образующий многочлен следует помнить, что длина остатка должна быть не меньше числа контрольных разрядов, поэтому в случае нехватки разрядов в остатке к остатку приписывают справа необходимое число нулей.

Остатки 011 110 111 101 001 010 100 011 110 и т. д.,

Пример.

10000000000 ½ 1011

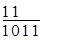1011

01100 11111+

1011

1110

1011

1010

1011

1000

1011

начиная с восьмого, остатки будут повторяться.

Остатки от деления используются для построения образующих матриц, которые, благодаря своей наглядности и удобству получения производных комбинаций, получили широкое распространение для построения циклических кодов. Построение образующей матрицы сводится к составлению единичной транспонированной и дополнительной матрицы, элементы которой представляют собой остатки от деления единицы с нулями на образующий многочлен P(x). Напомним, что единичная транспонированная матрица представляет собой квадратную матрицу, все элементы которой ‑ нули, кроме элементов расположенных по диагонали справа налево сверху вниз (в нетранспонированной матрице диагональ с единичными элементами расположена слева направо сверху вниз). Элементы дополнительной матрицы приписываются справа от единичной транспонированной матрицы. Использоваться могут лишь те остатки, вес которых W ³ d₀ - 1, где d₀ ‑ минимальное кодовое расстояние. Длина остатков должна быть не менее количества контрольных разрядов, а число остатков должно равняться числу информационных разрядов.

Строки образующей матрицы представляют собой первые комбинации исходного кода. Остальные комбинации кода получаются в результате суммирования по модулю 2 всевозможных сочетаний строк образующей матрицы.

Пример.

Построить полную образующую матрицу циклического кода, обнаруживающего все одиночные и двойные ошибки при передаче 10-разрядных двоичных комбинаций.

Решение.

По таблице 3.4.1 выбираем ближайшее значение k ³ 10.

Таблица 3.4.1 – Соотношения между информационными и проверочными символами для кода длиной до 16 разрядов

n	k	ρ	n	k	ρ

Согласно таблице таким значением будет k = 11, при этом r = 4, а

n = 15. Также выбираем образующий многочлен x⁴ + x³ +1.

Полную образующую матрицу строим из единичной транспонированной матрицы в канонической форме и дополнительной матрицы, соответствующей проверочным разрядам.

Транспонированная матрица для k = 11 имеет вид:

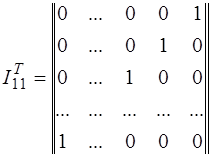
Дополнительная матрица может быть построена по остаткам деления комбинации в виде единицы с нулями (последней строки единичной транспонированной матрицы) на выбранный образующий многочлен:

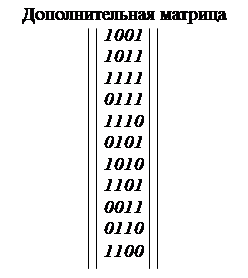100000000 11001

11001

10010

11001

10110

11001

11110

11001

011100

11001

010100

11001

11010

11001

0011000

11001

0001

Полная образующая матрица будет иметь вид:

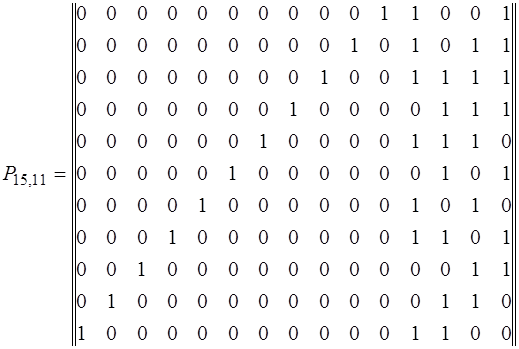
Описанный выше метод построения образующих матриц не является единственным. Образующая матрица может быть построена в результате непосредственного умножения элементов единичной матрицы на образующий многочлен. Это часто бывает удобнее, чем нахождение остатков от деления. Полученные коды ничем не отличаются от кодов, построенных по образующим матрицам, в которых дополнительная матрица состоит из остатков от деления единицы с нулями на образующий многочлен.

Образующая матрица может быть построена так же путем циклического сдвига комбинации, полученной в результате умножения строки единичной матрицы ранга k на образующий многочлен.

Ошибки в циклических кодах обнаруживаются при помощи остатков от деления полученной комбинации на образующий многочлен. Остатки от деления являются опознавателями ошибок, но не указывают непосредственно на место ошибки в циклическом коде.

Идея исправления ошибок базируется на том, что ошибочная комбинация после определенного числа циклических сдвигов “подгоняется” под остаток таким образом, что в сумме с остатком она дает исправленную кодовую комбинацию. Остаток при этом представляет собой не что иное, как разницу между искаженными и правильными символами, единицы в остатке стоят как раз на местах искаженных разрядов в подогнанной циклическими сдвигами комбинации. Подгоняют искаженную комбинацию до тех пор, пока число единиц в остатке не будет равно числу ошибок в коде. При этом, естественно, число единиц может быть либо равно числу ошибок s, исправляемых данным кодом (код исправляет 3 ошибки и в искаженной комбинации 3 ошибки), либо меньше s (код исправляет 3 ошибки, а в принятой комбинации 1 ошибка).

Место ошибки в кодовой комбинации не имеет значения. Если k ³ (n / 2), то после определенного количества сдвигов все ошибки окажутся в зоне “разового” действия образующего многочлена, т. е. достаточно получить один остаток, вес которого W £ s, и этого уже будет достаточно для исправления искаженной комбинации.

Подробно процесс исправления ошибок рассматривается ниже на примерах построения конкретных кодов.