Ньютонның бірінші интерполяциялық формуласы

Есептің қойылуы.Айталық 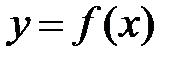функциясының, тәуелсіз айнымалылары бір-бірінен бірдей қашықтықта жатқан 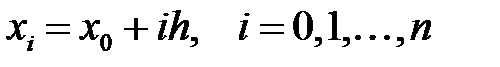мәндерінде, 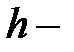интерполяция қадамы, мәндері 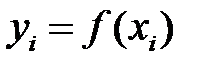берілсін. Дәрежесі 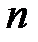-нен аспайтын және 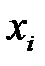нүктелерінде 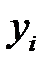-ге тең болатын, яғни 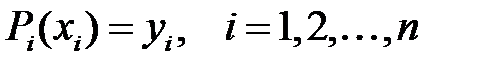, (1) орындалатын 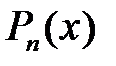полиномын табу (құру) керек.

(1)-ші шарты келесі шартқа эквивалентті

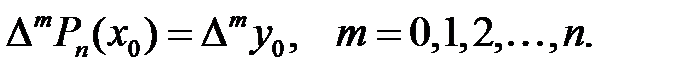(2)

Ньютон мырза полиномды келесі түрде іздеген

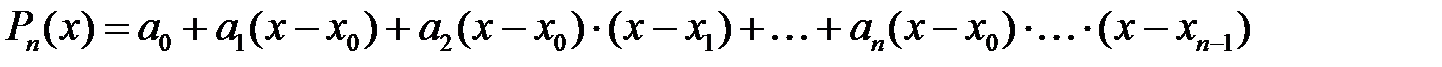. Жалпыланған дәрежені қолдансақ

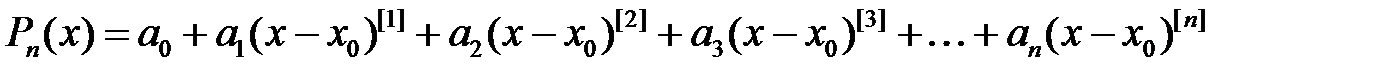. (3)

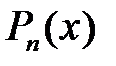полиномының 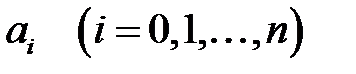коэффициенттерін анықтайық. Ол үшін 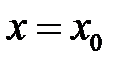деп алып, (3) формуладан алатынымыз:

.

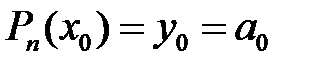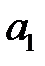коэффициентін анықтау үшін бірінші ақырлы айырымын құрайық

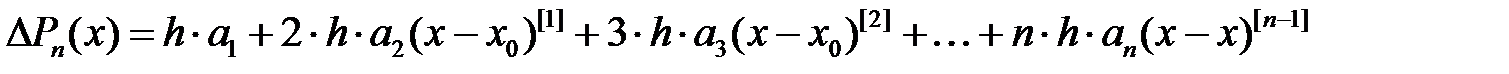. Енді 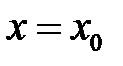деп алып, табатынымыз: 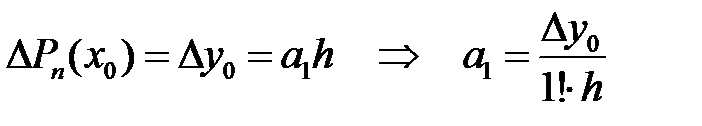. 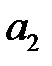-ні табу үшін екінші ақырлы айырымын құрамыз, яғни 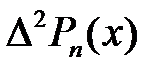-ті есептейміз:

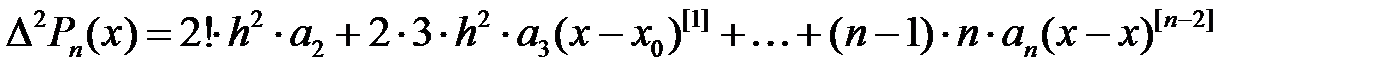. Енді 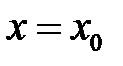деп алып, табатынымыз: 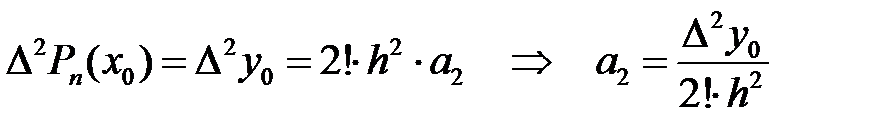. Осы процесті жалғастыра отырып, 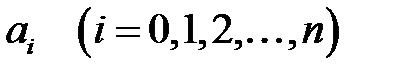барлығын табамыз

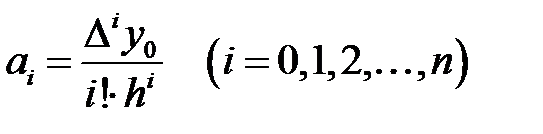, мұнда .

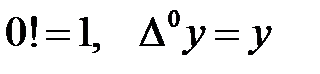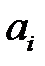коэффициенттерін (3) формулаға қойып, Ньютонның бірінші интерполяцияляқ полиномын аламыз

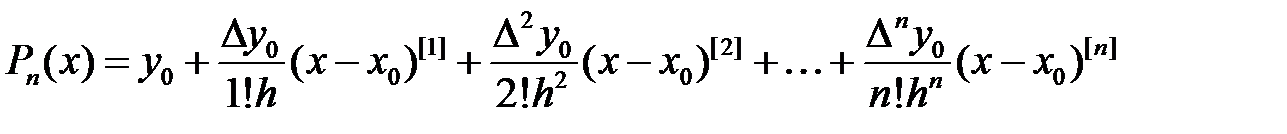. (4)

Осы полином қойылған талаптың барлығына да сәйкес келеді. Расында да, 1) 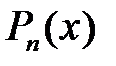-тің дәрежесі 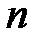-нен аспайды, 2) 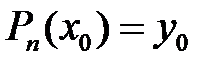және 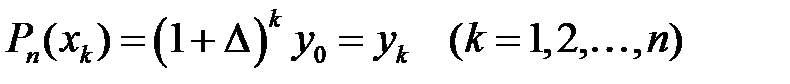. Соңғы тұжырымды өздеріңіз дәлелдеңіз.

Ньютонның екінші интерполяциялық формуласы.

Есептің қойылуы өзгермейді, яғни Ньютонның бірінші интерполяциялық формуласы сияқты формула табу керек. Мұнда да деп аламыз да, интерполяциялық полиномды келесі түрде іздейміз

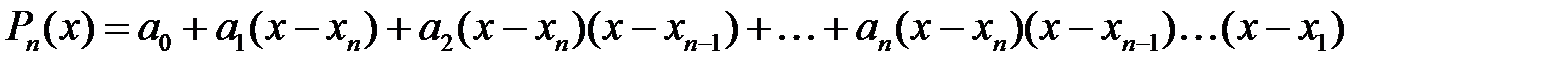. Белгісіз коэффициентері 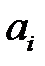-лерді табу үшін біз Ньютонның бірінші формуласындағы 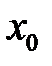-ді 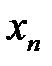-ге ауыстырып, барлық амалдарды орындаймыз. Сонда алатынымыз:

Бұдан шығатыны

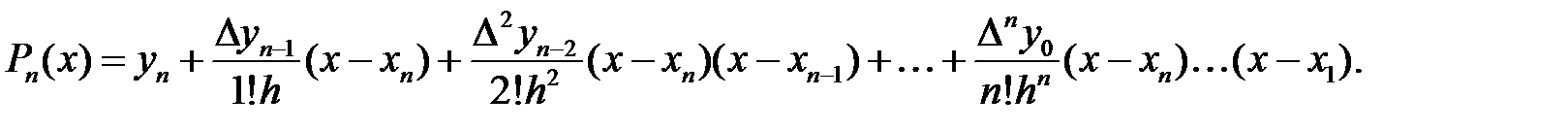Немесе 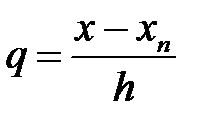десек, онда 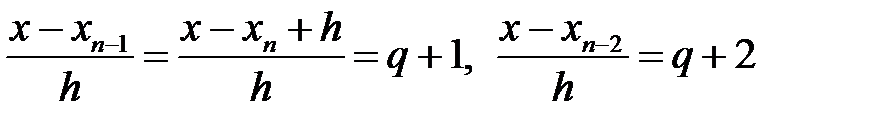, т.с.с. соңғы формуладан алатынымыз:

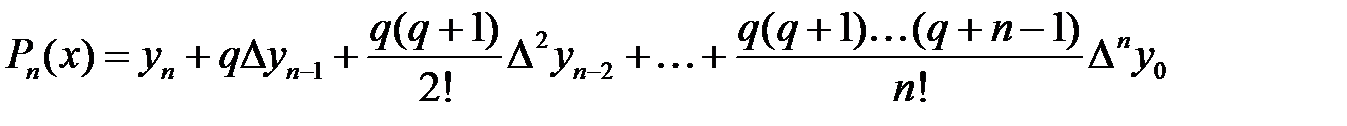. Бұл Ньютонның екінші, немесе артқа интерполяциялық формуласы. Белгісіз функция 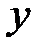-ті жуықтау үшін 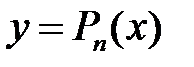дейміз

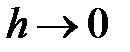-да байқайтынымыз 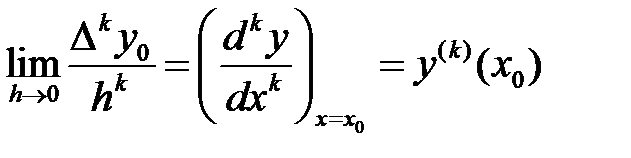және 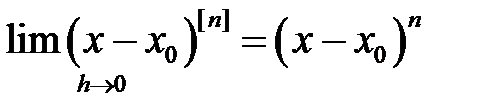. Осыларды ескере отырып, (4)-тен алатынымыз 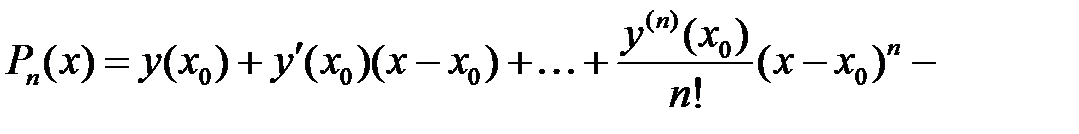Тейлор полиномы.

Іс жүзінде, немесе жеке компьютерде есеп шығарғанда, Ньютонның келесі, бірінші (алға), полиномын пайдаланамыз. Ол үшін, алдымен 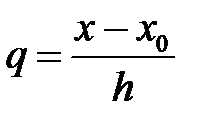жаңа айнымалысын енгіземіз. Ендеше 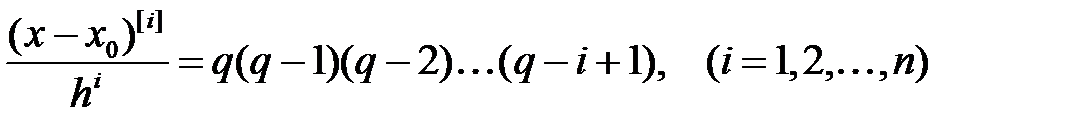. Бұдан 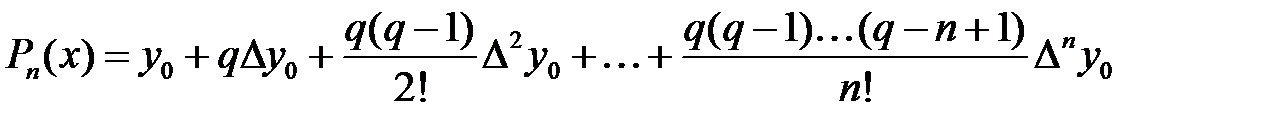, (5)

мұндағы 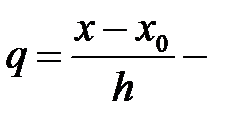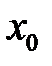нүктесінен бастап 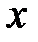нүктесіне жету үшін қажетті қадамдар саны. (5) формуласы Ньютонның бірінші, немесе алға формуласы деп аталады. Бұл формуланы 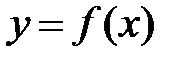функциясын 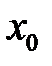нүктесіне жақын маңайда қолданған жөн. Мұндағы 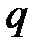модулі бойынша өте аз шама.

Ньютон әдісінде шешімнің бар болуы және жинақтылығы

Жартылай бөлу әдісімен қатар күрделі және тиімді итерациялық әдістер бар. Бұл әдістерге Ньютон есімімен байланысқан әдістердің тобы қатысады. Олардың екеуін қарастырайық: жанама әдісі және хорда (қиюшы) әдісі. Бл әдістердің екеуі де мынадай тәсілге негізделген.

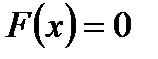
теңдеуінің 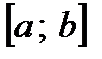кесіндісінде жалғыз түбірі бар болсын. Оны оған мәндес теңдеуге түрлендіреміз:

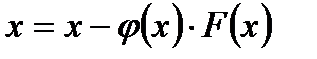
мұндағы, 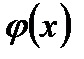- 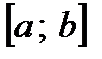кесіндісінде анықталған және осы кесіндіде нөлге айналмайтын кез келген функция.

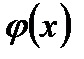- ті әртүрлі тәсілмен таңдай отырып, көрсетілген әдістерді алуға болады.

Жанама әдісі

а) Бірінші тәсіл

Айталық 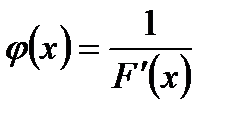. Сонымен итерациялық тізбек

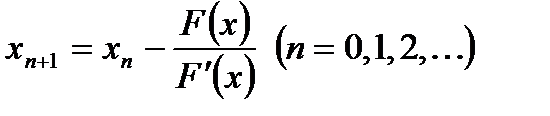
реккуренттік қатынасының көмегімен құрылады. Бастапқы 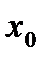мәнін таңдау мәселесі, 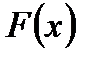функциясының мынадай шарттарды қанағаттандыруымен шешіледі:

1) 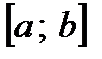кесіндісінде екінші рет дифференциалданады;

2) Бірінші және екінші ретті туындылары осы кесіндіде таңбасын сақтайды, яғни 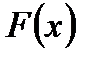функция монотонды және дөңестік сипатын ауыстырмайды.

Мұндай жағдайда 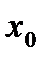мәні ретінде 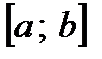кесіндісінің шеткі нүктелерінің бірі алынады және ол нүктеде 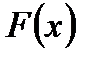функциясы және оның екінші ретті туындысы бірдей таңбалы болуы керек, яғни 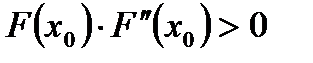шарты орындалады.

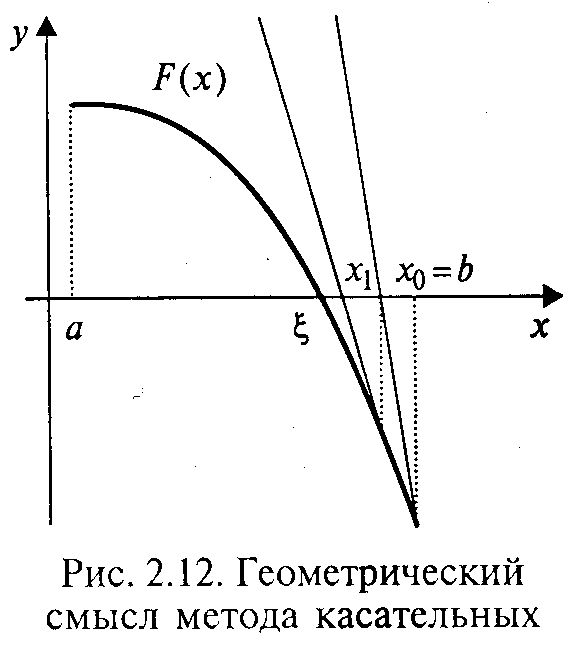Реккуренттік қатынаспен ( 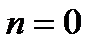) болғанда анықталған 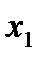нүктесі, 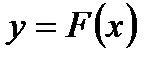функциясының графигіне 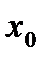нүктесінде жүргізілген жанамамен абсциссаның қиылысу нүктесі болады.

Итерациялық тізбектің әрбір келесі мүшесіне 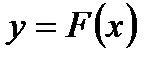функциясының графигіне тізбектің алдыңғы мүшесі арқылы жүргізілген жанаманың абсциссамен қиылысу нүктесі сәйкес келетін болады.

Қателікті бағалау мынадай теңсіздіктің көмегімен жүзеге асырылады:

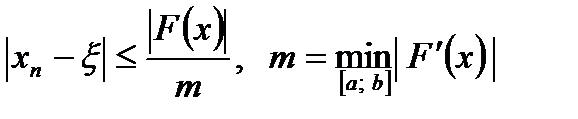
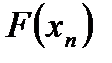мәндері реккуренттік тізбектің мүшелерін табуда есептелетін болады.

14. Ең жылдам түсу әдісі және оның жинақтылығы.

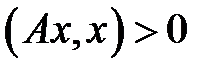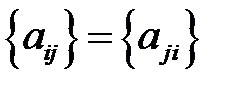, матрицасы үшін (1) жүйені шешудің тиімді процесі (әдісі) қателік функциясының нөлге ұмтылуынан шығады:

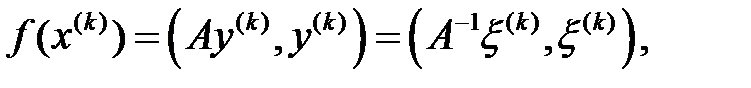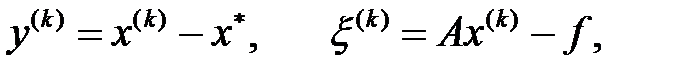
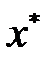
мұндағы 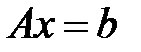жүйесінің дәл шешімі, 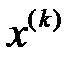– жуық шешімі. Әрқашан 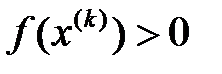, , 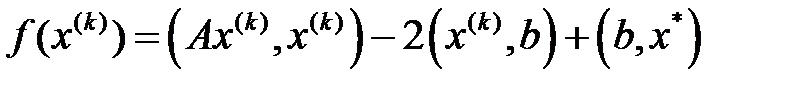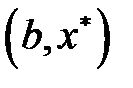– белгісіз. Сондықтан да ,

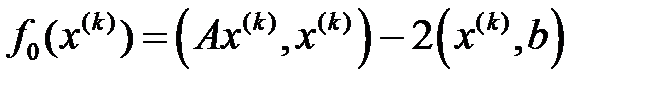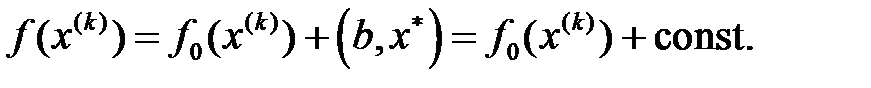
Яғни, 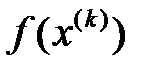функциясының кемуі 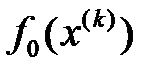функционалының кемуіне эквивалентті. 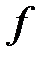, немесе 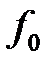, градиентке қарсы бағытта кемитіні белгілі. Және де 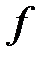градиентіне қарсы бағытта ең жоғарғы жылдамдықпен кемиді. 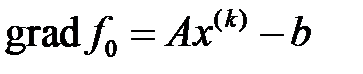шамасын есептеуге болады. 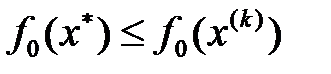болатыны анық, сондықтан функционал минимумына 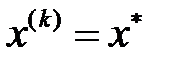болғанда жетеді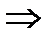 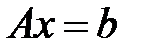жүйесін шешу есебі 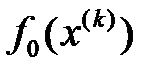функционалын минимизациялау есебіне эквивалентті.

Есеп шешуі. 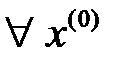алынып, осы 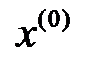нүктесіне 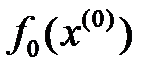функционалының 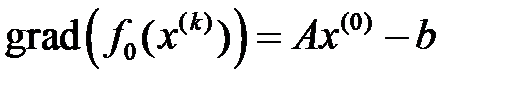градиентіне қарсы бағыт есептелінеді. Осы 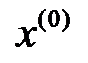нүктесінен 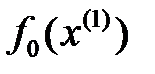минималды болатын 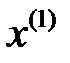нүктесіне дейін таңдап алынған бағытта қозғаламыз, яғни келесі 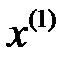жуықтауы 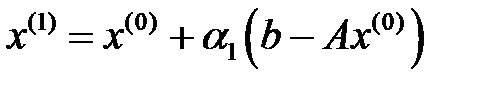түрінде ізделінеді, және де 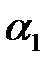коэффициенті берілген 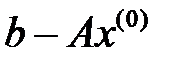бағытында, 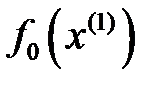функционалының минимумы шартынан, таңдалынады. Енді 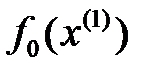есептейік:

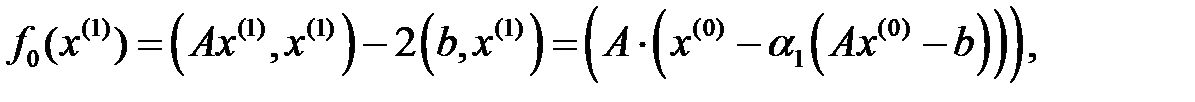
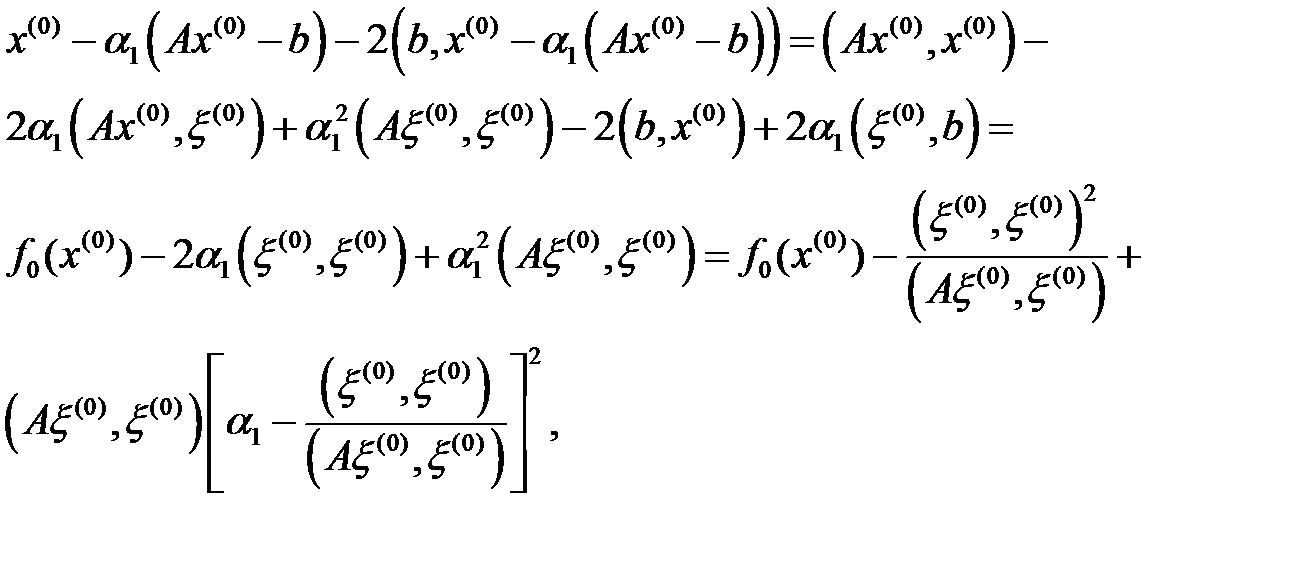
мұндағы, 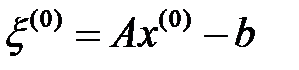. 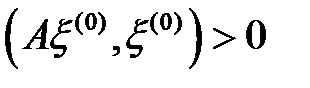болғандықтан, 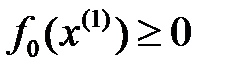өрнегі өзінің минимумына 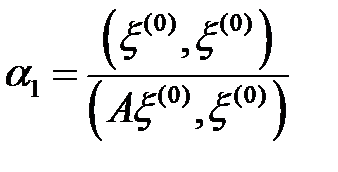нүктесінде жетеді. Және бұл минимум 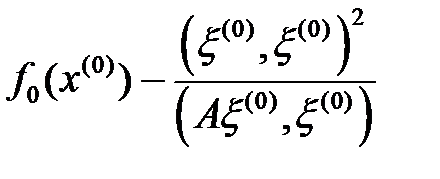мәніне тең. Ары қарай, 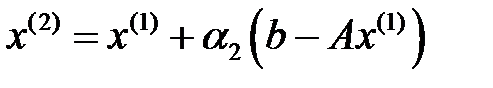өрнегін анықтаймыз және 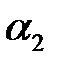санын 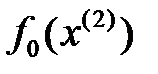өрнегінің минимум шартынан табамыз 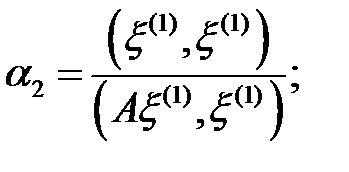мұндағы, 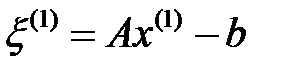, т. с. с. Осылардан келесі алгоритмді аламыз:

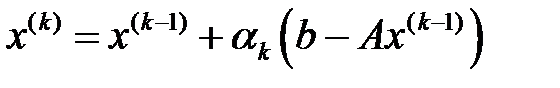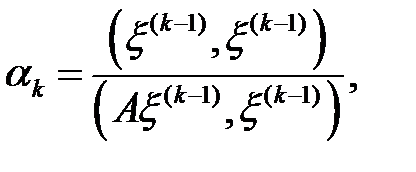
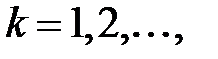
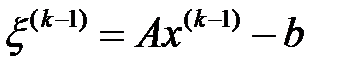, . Бұл жағдайда .

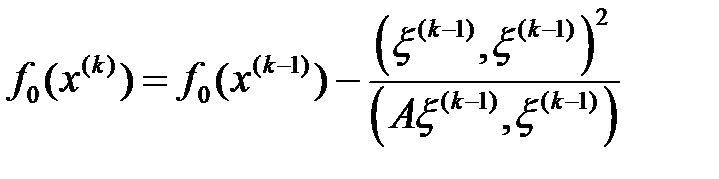Теорема. Ең жылдам түсу әдісі үшін 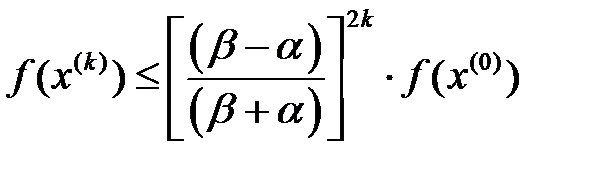бағасы орындалады. Мұндағы .

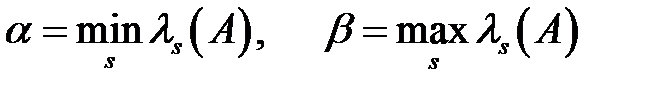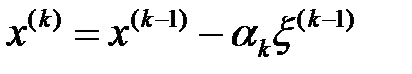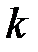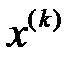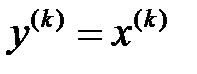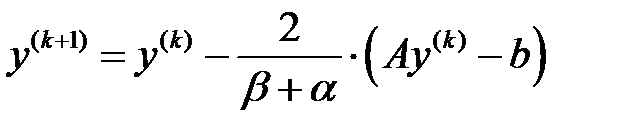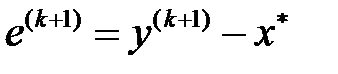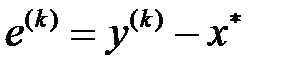Дәлелдеуі. Айталық болсын, – бекітілген сан. алдыңғы итерациясын пайдаланып, яғни деп алып, тағы бір тиімді итерациялық процесін жүргізейік : . Онда қателік векторлары және тиімді итерациялық процесс үшін 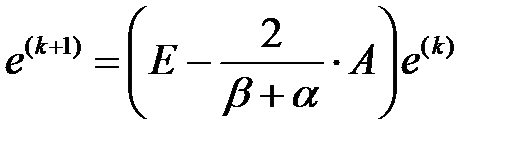қатынасымен байланысады.

Айталық 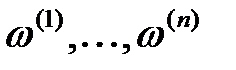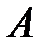матрицасының 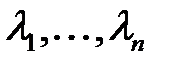меншікті сандарына сәйкес келетін, яғни 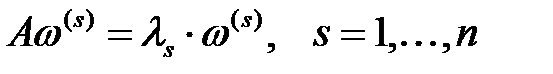, ортогональ және ортонормаль меншікті векторлары болсын. Бұл жағдайда,

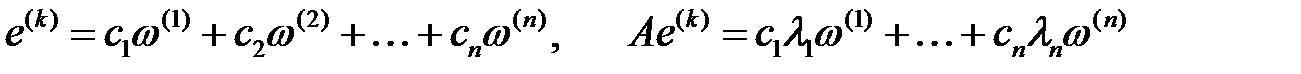және

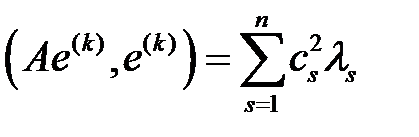. Ары қарай,

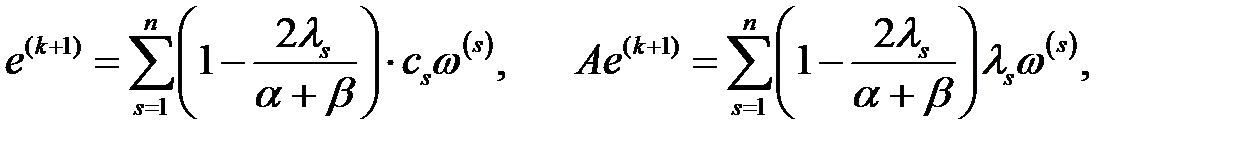
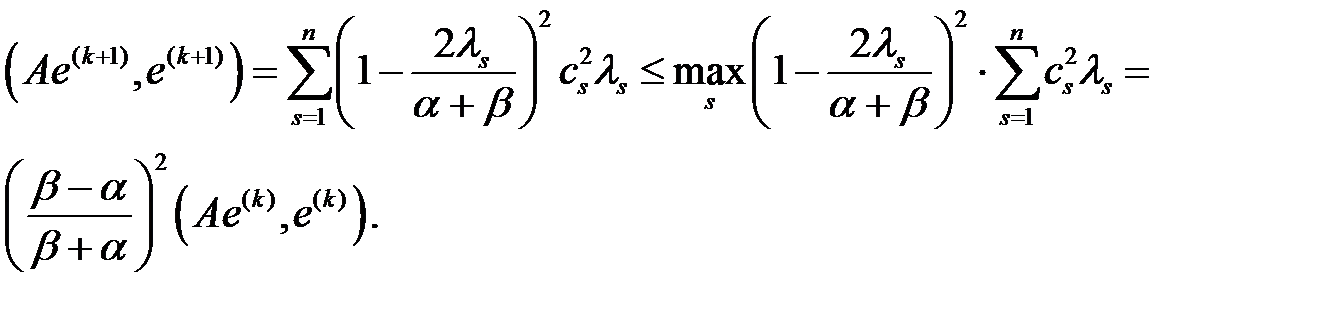
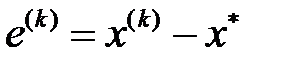болғандықтан 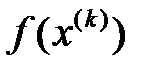үшін соңғы теңсіздіктен алатынымыз: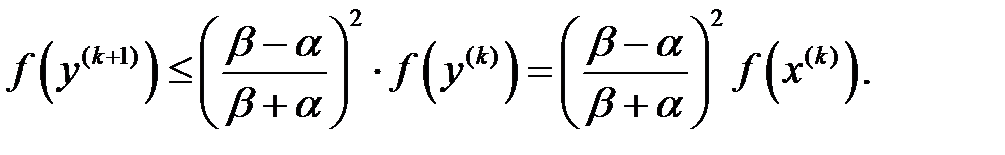

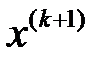ең жылдам түсу әдісімен алынған келесі жуықтауы болсын, онда 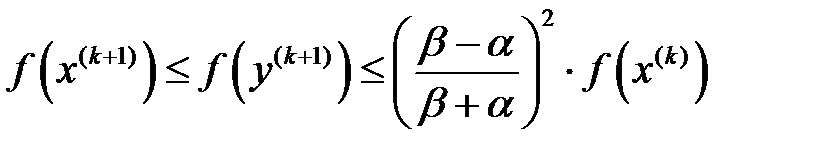болатыны анық.

Осы теңсіздікке индукция әдісін қолданып, теорема тұжырымын аламыз. Шынында да 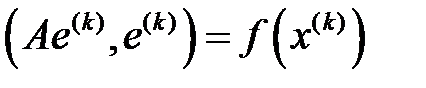болғандықтан, 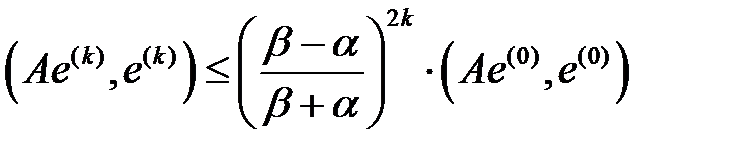. Келесі 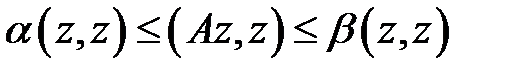Релей теңсіздігінде, бір рет 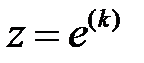(сол жағынан), екінші рет 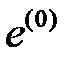(оң жағынан) деп пайымдап алатынымыз:

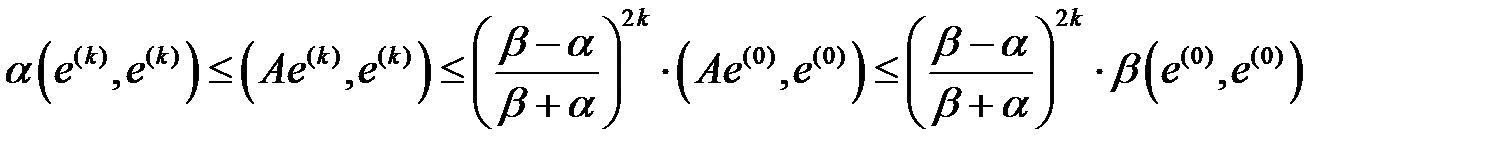
немесе

.

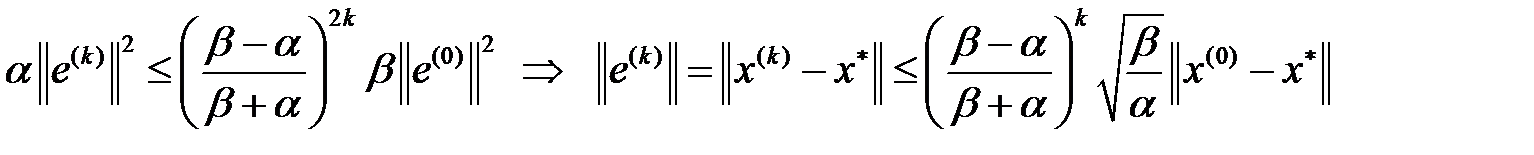Бұл алынған өрнек – ең жылдам түсу әдісінің жинақтылық жылдамдылығының бағасы.