Надежности сложных комбинированных систем
В технике иногда применяют комбинированные системы, которые нельзя свести ни к последовательным, ни к параллельным. Рассмотрим основную систему из двух элементов  , которая дублирована системой
, которая дублирована системой  (смотри рисунок 1.11). Кроме того, предусмотрен дополнительно резервный элемент
(смотри рисунок 1.11). Кроме того, предусмотрен дополнительно резервный элемент 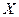 , который резервирует элементы
, который резервирует элементы  и
и  , и делает систему сложной.
, и делает систему сложной.

Рисунок 1.11 – Система со сложным резервированием
Для расчета подобных сложных систем пользуются теоремой полной вероятности Байеса, которая в применении к надежности формулируется так.
Вероятность отказа системы равна
 (
( 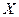 работоспособен)
работоспособен)  +
+  (
( 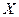 неработоспособен)
неработоспособен)  ,
,
где  и
и  – вероятность работоспособности и отказа элемента
– вероятность работоспособности и отказа элемента 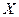 . Структура формулы понятна, так как
. Структура формулы понятна, так как  и
и  можно представить как долю времени при работоспособном и соответственно неработоспособном элементе
можно представить как долю времени при работоспособном и соответственно неработоспособном элементе 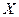 .
.
Вероятность отказа системы при работоспособности элемента 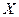 определяют как произведение вероятности отказов обоих элементов, т. е.
определяют как произведение вероятности отказов обоих элементов, т. е.
 (
( 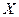 работоспособен)
работоспособен)  .
.
Вероятность отказа системы при неработоспособности элемента 
 (
( 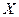 неработоспособен)
неработоспособен)  .
.
Вероятность отказа системы в общем случае
 .
.
В сложных системах приходится применять формулу Байеса несколько раз.
