Рівняння нерозривності (суцільності) потоку

Лекция 2. ГІДРОДИНАМІКА

План

2.1 Основні терміни та поняття

2.2 Рівняння нерозривності (суцільності) потоку

2.3 Диференціальні рівняння руху ідеальної рідини (рівняння ейлера).

2.4 Рівняння Бернуллі для усталеного потоку ідеальної рідини, яка знаходиться під дією лише сили ваги

2.5 Витікання рідини крізь отвір у тонкій стінці

Основні терміни та поняття

Гідродинаміка – розділ гідравліки, який вивчає закони руху рідини та взаємодію між рідиною та твердими тілами за їх відносним рухом.

В інженерній практиці використовується об'єм рідини скінчених розмірів, що рухається, який має назву потік. Потік може бути стаціонарним або усталеним в умовах, коли параметри його не змінюються в часі. Неусталений, або нестаціонарний потік має параметри, які змінюються в часі.

У прикладній гідравліці струминну модель називають одновимірною, оскільки вважають, що параметри швидкості, тиску тощо залежать тільки від однієї геометричної координати. Реальні потоки скінчених розмірів не одномірні через вплив в'язкості й межових поверхонь. Відночас деякі потоки, вивчення яких має практичне значення, можна замінити одновимірними моделями. Наприклад, стікання в циліндричних трубах, де швидкості в перерізі розподілені нерівномірно, можна замінити рухом із середньою швидкістю, однаковою для всіх точок даного перерізу.

Об'єм рідини, який проходить через переріз потоку за одиницю часу, називається об'ємною витратою

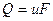, (2.1)

де u – середня швидкість потоку, яка нормальна до перерізу;

F – площа перерізу потоку.

Швидкість u приймається сталою по усій площі перерізу.

Рівняння нерозривності (суцільності) потоку

Розглянемо усталений потік ідеальної (нестисливої) рідини в каналі (рис. 2.1) Вважаємо, що бічна поверхня каналу непроникна, та приймаємо гіпотезу суцільності рідини, коли всередині об'єму не виникає поглинання маси чи її генерації. В цьому випадку об'єми рідини, які проходять крізь перерізи 1 – 1 і 2 – 2 за час t, дорівнюють W₁= W₂ або Q₁t = Q₂t, тобто Q₁ = Q₂. Тоді рівняння нерозривності (суцільності) потоку набирає вигляду

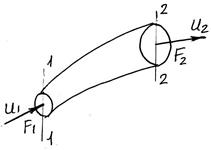
Рисунок 2.1 – Потік ідеальної (нестисливої) рідини в каналі

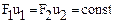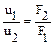або (2.2)

Це рівняння виражає сталість масової витрати рідини вздовж потоку.

Одиниця вимірювання витрати м³/с, однак для практичних розрахунків в машинобудуванні використовується несистемна одиниця л/хв тобто літри в хвилину.

Вираз (2.2) слушний лише для ідеальної рідини. Розглядаючи реальні рідини, треба мати на увазі, що вони стисливі, тобто об'єми W₁ ≠ W₂, а в наслідок внутрішнього тертя швидкості в різних точках перерізу потоку не однакові і розподілені за різними законами.

2.3 Диференціальні рівняння руху ідеальної рідини (рівняння ейлера)

Основне рівняння гідродинаміки потоку ідеальної рідини.

Розглянемо усталений потік ідеальної (нестисливої та нев'язкої) рідини. В такому потоку сили внутрішнього тертя відсутні. Для умов рівноваги рідини одержано систему рівнянь Ейлера для гідростатики (1.1)

Щоб знайти рівняння руху, скористаймося принципом Даламбера, тобто необхідно до діючих сил додати сили інерції, які віднесені до одиниці маси (одиничні сили інерції).

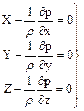
Відповідні сили інерції в напрямку осей дорівнюють

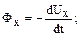
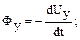
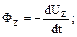
де U_x, U_y, U_z – проекції швидкості на осі x, y, z, а t – час.

Додаємо ці сили

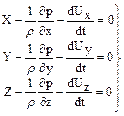(2.3)

Рівняння (2.3) мають назву диференціальних рівнянь Ейлера для гідродинаміки нев'язкої рідини.

Перетворимо систему (2.3) таким чином. Помножимо кожну строчку системи на відповідні переміщення dx, dy, dz і додамо

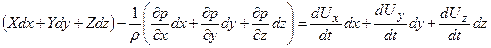
або

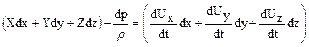(2.4)

Вираз в дужках в правій частині можна спростити.

Переміщення dx, dy, dz являють собою добутки проекції швидкості на час dx = U_xdt; dy = U_ydt; dz = U_zdt;

Таким чином вираз в дужках буде мати вид

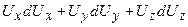
маючи на увазі, що

; ;

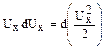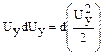сума дорівнює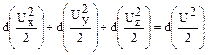

тобто являє собою повний диференціал функції швидкості.

Вирішуючи рівняння (1.14) відносно dp, маємо

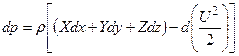. (2.5)

Рівняння (2.5) має назву основного рівняння гідродинаміки в диференціальній формі. Тиск в довільній точці ідеальної рідини, яка рухається, є функція координат цієї точки і швидкості її руху.