Алгебра отношений, модель, графы и мографы;

Алгебра отношений

Отображение, хⁿ→Х называется n-местной операцией. При n=2 – бинарная операция :х²=хRх→х

Множество А вместе с заданной на нем совокупностью операций, т.е. 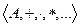называется алгеброй

Отношение — математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Отношения обычно классифицируются по количеству связываемых объектов (арность) и собственным свойствам (симметричность, транзитивность и пр.). В математике примерами отношений являются равенство (=), коллинеарность, делимость и т. д.

n-местным (n-арным) отношением, заданным на множествах M₁, M₂, … M_n, называется подмножество прямого произведения этих множеств.

Термин «алгебра отношений» используется как синоним термина «логика отношений». Раздел логики, изучающий высказывания об отношениях между объектами разной природы, называется логикой отношений.

На языке теории множеств и алгебры n-местным (n-арным, в частности, бинарным) отношением называется множество (класс) упорядоченных систем из n элементов (упорядоченных n-ок, соответственно — упорядоченных пар) членов некоторого множества. Это множество называется полем данного отношения.

Свойства отношенийрассмотрим на примере свойств бинарных отношений:

А - множество, ρ - отношение на А.

1) R - рефлексивно, если для любого хÎА имеем хRх, т.е. х находится в отношении сам с собой.

2) R - симметрично, если хRy ==> yRх.

3) R - антирефлексивно, если не существует хÎА: хRх, т.е. R выполняется только для не совпадающих элементов.

4) R - не рефлексивно, если существует хÎА такой, что (х,х) не принадлежит R.

5) R - асимметрично, если из xRy и yRx хотя бы одно не выполняется.

6) R - антисимметрично, если для любых (x,y)ÎА из того, что xRy и yRx ==> х=y (≤).

7) R - транзитивно, если для любых x,y,z ÎA выполняется: из xRy и yRz ==> xRz

Для отношений определяются понятия области определения данного отношения и области его значений. Множество первых элементов упорядоченных пар (xRy), входящих в отношение R, составляет его область определения (область отправления). Множество их вторых элементов составляет область значений (область прибытия).

Поскольку отношения являются частными случаями множеств, для них вводятся операции объединения (суммы), пересечения (произведения) и дополнения отношений.

Тория графов.

Граф - совокупность двух множеств V(точек) и E(линий), между элементами которых определено отношение инцидентности (Вершина V и ребро E называются инцидентными, если V является одним из концов ребра E. Дуга называется инцидентной вершине V, если она или заходит в V или исходит из V. ).

Пусть V - некоторое множество, V≠ Ø. V(2) - множество всех его двуэлементных подмножеств. V(2)= {(U,V)|U,VєV, неупорядоченная пара (U,V)}.

Множество V задаёт множество вершин графа G, а множество E -множество ребер. Если |V| = p, |E| = q, то Gp,q или (p,q) - граф.

• Две вершины графа смежны, если они соединены ребром;
• Два ребра смежны, если они имеют общую вершину;
• Вершина V и ребро L называются инцидентными, если V является одним из концов ребра L.;
• Если множество V - конечно, то граф называется конечным.

Способы задания графов

1. Перечисление множеств вершин V и ребер E, задающих граф G.

2. Графический: множество V - точки плоскости, изображающие вершины; множество E - отрезки прямой(кривой) линии, изображающие рёбра.

3. Матрица смежности:

Пусть |V| = p, |E| = q, A = ||a_i,j||, i,j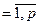

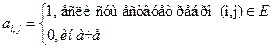
4. Матрица инциденций: B = ||bij||, i 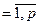j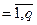

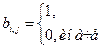если вершина i инцидента ребру j,