Алгебраическая, тригонометрическая и показательная формы записи комплексных чисел.

Алгебраическая форма

Запись комплексного числа в виде , , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что ):

Тригонометрическая и показательная формы

Если вещественную 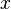и мнимую 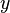части комплексного числа выразить через модуль и аргумент ( , ), то всякое комплексное число , кроме нуля, можно записать в тригонометрической форме

Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:

где — расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

42. Действия над комплексными числами

Сложение и вычитание

По аналогии со сложением и вычитанием векторов мы приходим к следующему правилу сложения и вычитания комплексных чисел:

(a₁ + b₁i ) + (a₂ + b₂i ) +...+ (a_n + b_ni ) = (a₁ + a₂+ ...+ a_n ) + (b₁+ b₂+...+ b_n )i = a + bi

Операция введена, так как получили элемент того же множества.

Вычитание определяется как действие, обратное сложению, то есть разность x +iy = (a₁ + b₁i) – (a₂ + b₂i ) определяется из условия:

(x +iy) + (a₂ + b₂i ) = (a₁ + b₁i) .

Из правила сложения получаем:

x +a₂ = a₁,
y +b₂ = b₁.

То есть x = a₁ – a₂, y = b₁ – b₂ и разность

(a₁ + b₁i ) – (a₂ + b₂i ) = (a₁ – a₂) + (b₁– b₂)i.

Умножение комплексных чисел

Определение.Произведением двух комплексных чисел называется такое комплексное число, модуль которого равен произведению модулей сомножителей, а аргумент – сумме аргументов сомножителей.

Это определение совершенно очевидно, если использовать показательную форму комплексного числа:

Пусть комплексные числа даны в алгебраической форме. Найдём их произведение: (a₁ + b₁i) (a₂ + b₂i ) =x +iy.

Имеем .

Согласно определению умножения можем записать:

.

Распишем: ,

,

.

Окончательно получим:

.

Отсюда следует правило умножения комплексных чисел в алгебраической форме: комплексные числа можно перемножать как многочлены.

Если z = а + b i – комплексное число, то число называется сопряжённым с числом z . Его обозначают при помощи черты над числом.

, но , следовательно, .

Деление комплексных чисел

.

Модуль частного равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя.

Если делимое и делитель даны в алгебраической форме, топравило деления таково: для того, чтобы разделить комплексное число(a₁ + b₁i ) на другое комплексное число (a₂ + b₂i ), то есть найти , нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.

.

В результате операции получили элемент того же множества. Значит, операция деления считается введённой.