Пример 1. Решить уравнение

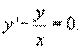
dy = y¢dx,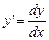

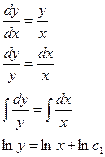
y = c₁ x¾ общее решение уравнения.

Пример 2. Доказать, что функция

у = С₁е^х + С₂е^2х (1)

является решением уравнения

у" – 3у' + 2у = 0. (2)

Решение. Последовательно дифференцируя (1), приходим к равенствам:

y' = С₁е^х + 2С₂е^2х,

у" = С₁е^х + 4С₂е^2х.

Решая эту систему относительно С₁е^хи С₂е^2х, получаем:

С₁е^х = 2y' – у",

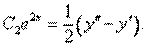
Подставляя эти выражения в (1), приходим к (2).

Пример 3. Проверить, что функция

у³ – Сх³ + 3ху = 0 (3)

является интегралом уравнения

у³ – (ху² + х²)у' + 2ху = 0. (4)

Решение. Дифференцируя (3)по х в предположении, что у = у(х), приходим к равенству

у²у' – Сх² + у + ху' = 0,

откуда

Сх² = (у² + х)у' + у.

Подставляя выражение для Сх² из последнего равенства в (3), имеем:

у³ – (у²y' + хy' + y)x + 3ху = 0,

что равносильно (4).

Пример 4. Найти дифференциальное уравнение семейства кривых

y = C(x – C)². (5)

Решение. Дифференцируя (5)по переменной х, получаем

y' =2C(x – C), (6)

откуда

С²= Сх – 5у'.(7)

С помощью равенства (7)преобразуем (5)так, что постоянная Сбудет входить в запись слагаемых полученного выражения встепенях не более первой:

у =0,5 ху' –0,5Су'.

Следовательно,

Су' = ху' – 2у. (8)

Умножая (6)на (у')², получаем

(у')³=2ху'(Су') – 2(Су')².

Исключая из полученного равенства Су' с помощью (8), окончательно имеем:

(у')³=4хyу' – 8y².

Пример 5. Найти решение уравнения

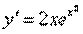
удовлетворяющие начальному условию у (0) = 1.

Решение. Из определения неопределенного интеграла <…>, следует, что общее решение заданного уравнения имеет вид:

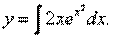
Используя преобразование переменной под знаком дифференциала, получаем

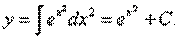
Учитывая начальное условие, приходим к равенству 1 = 1 + С, откуда С = 0. Таким образом, искомое частное решение имеет вид:

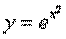
Геометрически найденная функция представляет интегральную кривую дифференциального уравнения, проходящую через точку (0, 1). ►

Пример 6. Решить уравнение:

yx²dy – ln xdx = 0.(10)

Решение. Исходное уравнение перепишем в виде

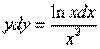. (11)

Таким образом, имеем уравнение с разделяющимися переменными и из (11) следует:

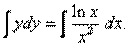
Интеграл левой части — табличный. Для нахождения интеграла правой части воспользуемся формулой интегрирования по частям, где

и = ln x, :

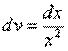
Окончательно интеграл уравнения (10) имеет вид:

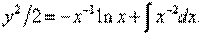
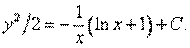
Пример 7. Решить уравнение

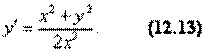
Решение. Правая часть уравнения является однородной функцией степени 0 по переменным х и у, так как

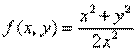
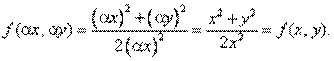
Поэтому данное уравнение — однородное. Для его решения воспользуемся заменой переменной z = у/х, где z = z (х). Тогда у' = zx y'=z'x + z, иуравнение (12.13) принимает вид:

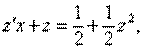
или

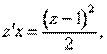
что равносильно

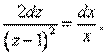
т.е. приходим к уравнению с разделяющимися переменными. Выполняя почленное интегрирование последнего равенства, получаем

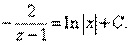
Возвращаясь к исходной переменной, после преобразования имеем:

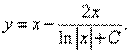
Пример 8:

1) (1 + x²)y" – 2ху' = 0.

Замена y' = p, p = p(x), y'' = p' Þ (1+ х²)p' – 2хр =0 — уравнение с разделяющимися переменными Þ

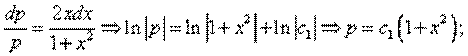
y' = c₁(1 + x²) Þ dy = c₁(1 + x²)dx Þ

y = c₁(x + x³/3) + c₂. ►

2) 1 + y'² –= 2yу''.

Замена y' = p, p = p(y), у" = р'р, 1 + р² =2урр' — уравнение с разделяющимися переменными

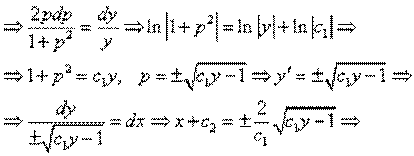
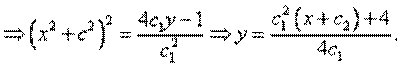
Пример 9:Решить уравнение

y" = y'ctg x.

Решение. Положим z = 1. Тогда у" = (у')' = z' и исходное уравнение принимает вид

z' = zctg x. (12.28)

Пусть z ≠ 0. Тогда из (12.28)следует:

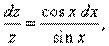
или

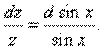
Интегрируя почленно последнее равенство, получаем

ln|z| = ln|sin x| + lnC₁,

где С₁ > 0, или

z = ± С₁sin x.

Так как z = 0 является решением уравнения (12.28),то произвольное решение этого уравнения имеет вид:

z = С₁sin x, (12.29)

где С₁— произвольное число.

Так как 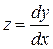то из (12.29)следует:

dy = С₁sin xdx.

Интегрируя последнее равенство, окончательно получаем

у = – С₁cos x + C₂. ►

Пример 10:Решить уравнение

yy" = y²y' + (y')²,

Решение. Пусть z = y', тогда , где и исходное уравнение принимает вид: dy

yzz' = y²z + z², (12.30)

т.е. становитсяуравнением относительно функции z = z(y). Очевидно, z = 0 — решение уравнения (12.30),откуда у = С,где С— произвольное число.

Пусть z ≠0. Тогда из (12.30)следует, что

yz' = y² + z (12.31)

— линейное уравнение первого порядка .Решение этого уравнения будем искать в виде z = uv,где v = v(y) — некоторое решение уравнения

yv' – v = 0, (12.32)

и = и(у) —решение уравнения

u'v = y. (12.33)

Решая (12.32),в частности, имеем v = у.Тогда (1233)приводит к уравнению и' =1, откуда и = у + С₁, т.е. решение (12.31)имеет вид:

z = y²+ C_]y.

Так как z = y',то приходим к уравнению

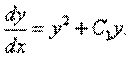
Пусть С₁ = 0. Тогда при y ≠0 имеем

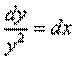
и, следовательно, х= у^–1 + С₂, или

у =(С₂ – х) ^–1. (12.34)

Пусть C₁ ≠ 0, тогда

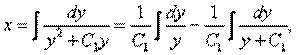
и после интегрирования:

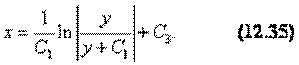
Окончательно решение исходного уравнения имеет вид у = С или (12.34), или(1235)

Пример 11.

xy¢ - y - x - 1= 0.

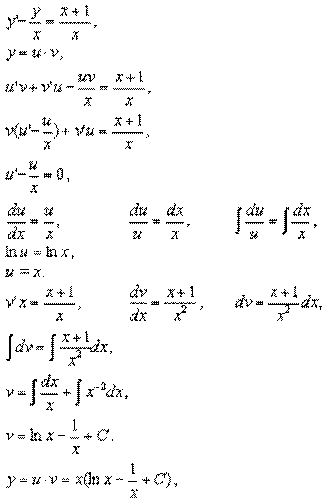
y = xln x + Cx - 1 ¾ общее решение уравнения.

Пример 12.

Решить уравнение

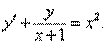
Решение. Будем искать решение этого линейного уравнения в виде

у = и × v,

где v = v(x)— некоторое решение уравнения

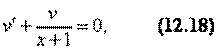
u = u(x)— решение уравнения

vu' = x². (12.19)

Уравнение (12.18)— с разделяющимися переменными:

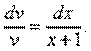
Выполняя почленное интегрирование последнего равенства, получаем:

ln|v| = –ln|x + 1| + C.

Поскольку в данном случае достаточно найти некоторое решение уравнения (12.18), то удобно полагать С =0, тогда

Подставляя найденную функцию v в уравнение (12.19),приходим к уравнению

du = (x³ + x²)dx.

В результате почленного интегрирования последнего равенства получаем

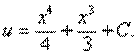
Таким образом, решение исходного уравнения имеет вид:

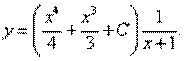
Пример 13.

Решить уравнение

(у³ – ху)у' = 1.

Решение. Будем искать решение этого уравнения в виде x = х(у) (т.е. считая, что у— независимая переменная, а х— функция от у). Так как

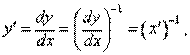
то исходное уравнение линейно относительно функции х:

х' + ху = у³. (12.20)

Решим соответствующее однородное уравнение:

х' + ху = 0. (12.21)

Пусть х ≠ 0. Тогда

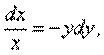
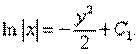
Последнее равенство равносильно

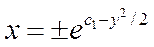
Учитывая, что х = 0 — решение уравнения (12.21),получаем, что общее решение этого уравнения имеет вид:

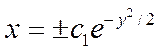12.22

Полагая, что С₂= С₂(у), найдем эту функцию из условия, что (12.22)— решение уравнения (12.20).Из (12.22)следует, что

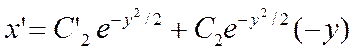12.23

Подставляя (12.22), (12.23)в (12.20), приходим к уравнению

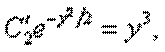
или

Тогда

Применяя формулу интегрирования по частям, получаем:

Подставляя найденное выражение для функции С₂= С₂(у)в (12.22), получаем решение уравнения (12.20):

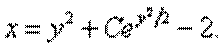
Пример 14.

Решить уравнение

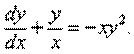
Решение. Данное уравнение является уравнением Бернулли при n = 2. Отметим, что у = 0 является решением этого уравнения. Пусть у ≠ 0. Воспользуемся заменой переменной z = у^{1 – n} = у^–1.Тогда у = z^–1, у' = – z^–2z' и исходное уравнение принимает вид:

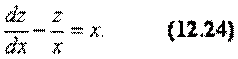
Решим сначала однородное уравнение

Пусть z ≠ 0. Тогда

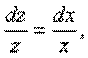
ln|z| = ln|x| = lnC₂, (12.26)

где С₂ — произвольное положительное число. Равенство (12.26) перепишем в виде:

|z| = С₂|х| или z = ± С₂х.

Учитывая, что z = 0 является решением уравнения (12.25), получаем, что произвольное решение этого уравнения имеет вид:

z = С₁х,(12.27)

где С₁— любое число.

Положим теперь, что С₁ = С₁(х)и найдем эту функцию С₁из условия, что (12.27) — решение уравнения (12.24). Из (12.27) следует, что

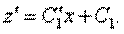
Тогда, учитывая (12.27), получаем, что уравнение (12.24) принимает вид:

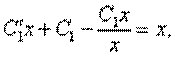
или

dC₁ = dx,

и поэтому

С₁ = х + С.

Подставляя это выражение в (12.27), имеем решение уравнения (12.24):

z = (x + C)x.

Так как

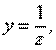
то окончательно решение исходного уравнения

имеет вид:

у(х²+ Сх) = 1,

или

y = 0.

Пример 15.Решить уравнения:

а) y'' – 3y' + 2y = 0;

Решая характеристическое уравнение

λ² – 3λ + 2 = 0,

находим его корни λ₁ = 1, λ₂ = 2. Тогда общее решение данного уравнения имеет вид

y = C₁e^x + C₂e^2x.

б) y'' – 2y' + y = 0

Решая характеристическое уравнение

λ² – 2λ + 1 = 0

получаем λ₁ = λ₂ = 1

Согласно п. 2 теоремы общее решение дифференциального уравнения имеет вид

y = (C₁ + C₂x)e^x.

в) y'' – 2y' + 2y = 0.

Характеристическое уравнение

λ² – 2λ + 2 = 0

не имеет действительных корней. В этом случае согласно п. 3 теоремы общее решение дифференциального уравнения имеет вид

y = C₁e^xsin x + C₂e^xcos x (a = β = 1).

Пример 16.

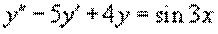
¾ неоднородное уравнение.

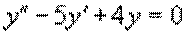
¾ соответствующее ему однородное уравнение.

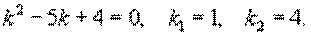
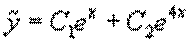
¾ общее решение однородного уравнения.

Будем искать частное решение неоднородного уравнения в виде

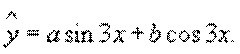
Подставим эту функцию в неоднородное уравнение:

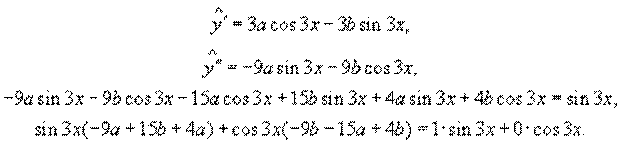
Приравняем коэффициенты при sinx и cosx.

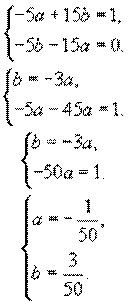
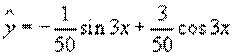
¾ частное решение неоднородного уравнения.

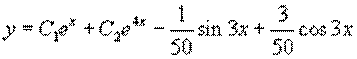
¾ общее решение неоднородного уравнения.

Пример 17.

у" + у' = 5х + 3.◄ Ищем решение в виде

.

а) y* — общее решение уравнения

у" + у' = 0,

его характеристическое уравнение

k² + k = 0, т.е. k₁= 0, k₂ = –1 Þ у* = с₁ + c₂e^{– x}:

б) — частное решение уравнения

у" + у' = 5х + 3

— ищем в виде

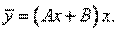
так как правая часть уравнения — многочлен первой степени и k₁= 0. Подставим в уравнение:

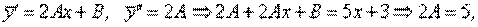
2A + B = 3 Þ A = 5/2, B = – 2.

Таким образом,

y = c₁ + с₂е^–x + 5х ²/2 – 2х

Основная литература

1. Шипачёв, В.С. Высшая математика: учебник для вузов.- 8-е изд., стер.- М.: Высшая школа, 2007.- 479с., илл. ББК 22.1 МО

2. Башмаков, М.И. Математика. Сборник задач профильной направленности: учеб. пособие для СПО.- М.: Академия, 2012.- 208с. ББК 22.1 ФИРО

3. Башмаков, М.И. Математика. Задачник: учеб. пособие для СПО.- М.: Академия, 2012.- 416с. ББК 22.1 ФИРО

4. Федорова Н.В. Математика. Учебное пособие. – Волгоградский институт бизнеса, вузовское образование. 2013. ISBN: 978-5-9061-7227-3

5. Лукша В.В. Математика. Учебное пособие. – Волгоградский институт бизнеса, вузовское образование. 2013. ISBN: 978-5-9061-7228-0

6. Гунько Ю.А. Математический анализ. Учебное пособие. – Волгоградский институт бизнеса, вузовское образование. 2013. ISBN: 978-5-9061-7230-3

7. Щербакова Ю.В. Дифференциальные уравнения. Учебное пособие. Научная книга. 2012.

8. Боронина Е.Б. Математический анализ. Учебное пособие. Научная книга. 2012.

Дополнительная литература

1. Высшая математика для экономистов: Учебник / Кремер Н.Ш. - М.: Юнити, 2006, 2008, 2009.

2. Сборник задач по высшей математике для экономистов: Учб. пособ./ Под ред. В.И. Ермакова-М.:ИНФРА-М,2004.

3. Общий курс высшей математики (для экономистов): Учебник / Под ред. Ермакова В.И. – М.: Инфра-М, 2003.

4. Кузнецов Б. Т. Математика. М., ЮНИТИ, 2004

Формы текущего контроля знаний: решение задач.

Формы контроля самостоятельной работы студентов: ответы на вопросы, проверка решения задач, заданных на дом.