Числа, допускающие построение циркулем и линейкой

Будем считать, что построения проводятся на выбранной раз и навсегда плоскости. Обычно задачи на построение в конечном счете сводятся к построению конечного числа точек, исходя из заданной совокупности конечного числа точек. Например, в задаче о трисекции угла задан угол, для чего достаточно задать три точки – вершину и две точки на сторонах; требуется разделить угол на три равные части, а для этого достаточно построить две точки, через которые проходят стороны, делящие угол.

Именно о таких задачах на построение циркулем и линейкой и пойдет речь в дальнейшем. При этом мы совершенно не будем говорить о методах построений – это вопрос чисто геометрический. Наша задача – выяснить, какие точки можно строить циркулем и линейкой, исходя из заданного конечного множества точек.

Выберем на плоскости произвольно прямоугольную декартову систему координат. Тогда каждая точка изображает комплексное число , и обычно множество точек плоскости отождествляют с множеством комплексных чисел. Если под сложением и умножением точек подразумевать сложение и умножение соответствующих чисел, то плоскость можно отождествлять даже с полем комплексных чисел, а поставленная задача может быть сформулирована в алгебраической форме: какие числа можно построить циркулем и линейкой на основании данного множества чисел.

Пусть 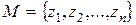- заданное множество чисел, а - есть наименьшее по включению числовое поле, содержащее множество 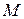и все числа, сопряженные с числами этого множества. Это поле будем называть исходным полем множества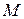

Основной результат формулируется в виде следующей теоремы:

Теорема. Комплексное число допускает построение циркулем и линейкой исходя из заданного множества чисел 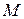тогда и только тогда, когда принадлежит исходному полю или некоторому пифагорову расширению этого поля.

Доказательство. Если задано множество 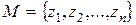, то легко также строятся сопряженные числа, так, что все числа множества будем считать известными.

В силу теоремы 2 § 4 каждое число исходного поля получается с помощью конечного числа операций сложения, вычитания, умножения, деления . Поэтому для доказательства возможности построения любого числа из поля достаточно доказать следующий результат: если известны (то есть заданы или построены) два числа – 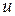и 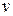, то можно построить также числа – .

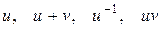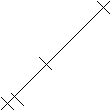
Для построения точки ( 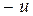) достаточно провести прямую через О и 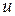и циркулем отложить отрезок от О до 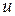по другую сторону от точки О (рис.1)

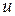
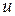
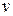
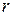
O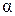

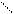
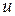О

О

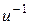
рис.1 рис. 2 рис. 3

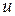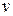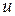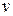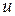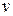Если точки О, , , не лежат на одной прямой, то для построения точки надо через точку провести прямую, параллельную прямой O , пересечение этих прямых и будет точкой (рис.2) Если же точки О, , лежат на одной прямой, то задача сводится к откладыванию заданных отрезков на этой прямой.

Пусть ,где , .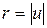

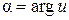Тогда

.

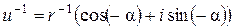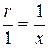
Для построения точки 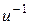достаточно построить аргумент и модуль числа 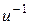. Для нахождения аргумента достаточно провести прямую (рис.3), а построение модуля – это построение четвертого пропорционального чисел 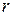, 1, 1; такая задача рассматривалась в школьном курсе математики.

Если , , 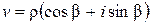то .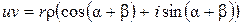

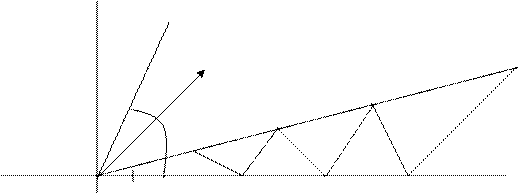
Аргумент числа 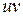строится путем последовательного откладывания углов 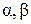, а модуль является четвертым пропорциональным чисел 1, , .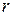

Итак, любое число исходного поля можно построить циркулем и линейкой.

rp

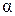
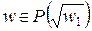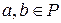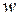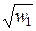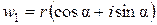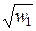Пусть теперь , где , . Тогда , где и построение числа сводится к построению . Поскольку , то мы считаем точку уже построенной. Если , то . Для построения аргумента числа достаточно разделить угол 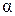пополам, что выполнимо циркулем и линейкой. Для построения же модуля надо построить среднее геометрическое чисел 1 и 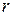; эта задача также рассматривается в школьном курсе геометрии.

1

Таким образом, любое число из простого пифагорова расширения можно построить циркулем и линейкой. Пусть теперь любое пифагорово расширение поля . Индукцией по 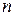докажем, что любое число этого поля можно построить. При это утверждение уже доказано. Предположим, что оно верно, для , т.е. любое число из поля 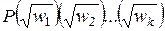допускает построение. Но так как есть простое пифагорово расширение поля 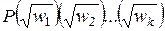, то согласно доказанному и любое число из допускает построение. Значит, наше утверждение верно при любом натуральном значении .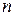

Теперь докажем, что всякое число, допускающее построение циркулем и линейкой, принадлежит исходному полю или некоторому пифагорову расширению этого поля.

Отметим, что циркулем и линейкой можно выполнять две операции: проводить прямую через две уже имеющиеся точки и строить окружность с центром имеющейся точке и проходящую через имеющуюся точку. Новые же точки могут быть получены в результате

пересечения таких прямых и окружностей.

Прямая, проходящая через точки 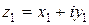, имеет уравнение

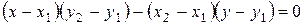
или

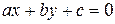
где числа 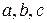рационально выражаются через числа .

Окружность с центром в точке , проходящая через точку 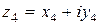, имеет уравнение

,

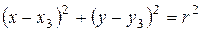где .

Пусть числа принадлежат исходному полю . Тогда в силу равенств

, ,

Заключаем, что действительные числа 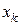и принадлежат полю 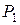, где 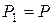, если и , если .

Отсюда заключаем, что коэффициенты уравнений прямых и окружностей с центрами в заданных точках, которые проходят через заданные точки, принадлежат полю .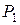

Пусть точка 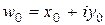получена при первом шаге построения циркулем и линейкой. Тогда есть решение одной из следующих систем уравнений с коэффициентами из поля :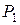

(1)

(2)

(3)

Если есть решение системы (1), то 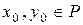, а, следовательно, и . Решение двух других систем сводится к решению квадратных уравнений с коэффициентами из поля 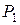. Если - дискриминант такого квадратного уравнения и , то , следовательно, и число принадлежит полю 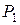. Если же , то принадлежит простому пифагорову расширению , которое в силу определения 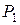, является также пифагоровым расширением поля .

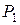Итак, точка , полученная при первом шаге построения на основании заданного множества чисел 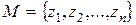, принадлежит полю 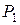, которое либо совпадает с , либо является его пифагоровым расширением. При следующем шаге построения получится новая точка, являющаяся решением одной из систем (1) – (3) с коэффициентами уже из поля . Согласно доказанному новая точка принадлежит либо полю , либо его пифагорову расширению, которое является также пифагоровым расширением исходного поля . Таким образом, и при втором шаге построения получается точка, принадлежащая либо исходному полю , либо его пифагорому расширению. Вполне понятно, что и любая точка 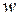, построенная после любого конечного числа шагов, принадлежит либо полю , либо некоторому пифагорову расширению этого поля.

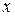
, а т.к. ,