Внецентренное действие продольной силы
8.2.1. Напряжения при внецентренном приложении нагрузки
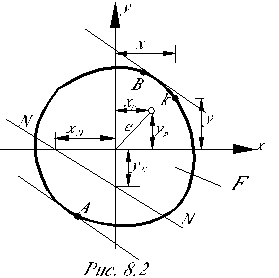 Сила Р приложена в точке с координатами – хр, ур.
Сила Р приложена в точке с координатами – хр, ур.
В этом случае говорят, что нагрузка по отношению к продольной оси z приложена с эксцентриситетом е (рис.8.2).
Напряжения в произвольной точке поперечного сечения определяются по формуле (8.3):
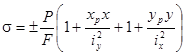 (8.3)
(8.3)
(+) перед выражением (8.3) соответствует внецентренному растяжению,
(–) - сжатию.
х, y – координаты точки, в которой определяются нормальные напряжения.
Условие прочности при внецентренном приложении нагрузки записывается для опасных точек А и В, наиболее удаленных от нейтральной линии.
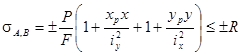 (8.4)
(8.4)
Здесь 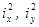 - квадраты радиусов инерции.
- квадраты радиусов инерции.
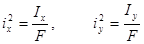
R – расчетное сопротивление материала растяжения или сжатия.
8.2.2. Уравнение нейтральной линии
На нейтральной линии нормальные напряжения равны нулю.
Приравняв нулю выражение (8.3) получим уравнения нейтральной линии
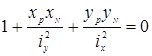 (8.5)
(8.5)
xN , yN – координаты точек, лежащих на нейтральной линии.
Решая полученное уравнение (8.5) в отрезках по осям координат, можно определить положение нейтральной линии.
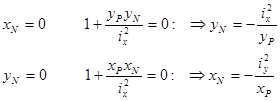 (8.6)
(8.6)
8.2.3. Ядро сечения
 Многие строительные материалы хорошо работают на сжатие и практически не воспринимают растягивающих деформаций: бетон, кирпичная кладка. Поэтому возникает задача определения такой области в поперечном сечении бруса, чтобы прикладываемая внутри нее нагрузка, вызывала по всему сечению напряжения одного знака. Такая область называется ядром сечения. Ядро сечения – область, расположенная вокруг центра тяжести сечения, приложенная внутри которой нагрузка, вызывает по всему поперечному сечению напряжения одного знака.
Многие строительные материалы хорошо работают на сжатие и практически не воспринимают растягивающих деформаций: бетон, кирпичная кладка. Поэтому возникает задача определения такой области в поперечном сечении бруса, чтобы прикладываемая внутри нее нагрузка, вызывала по всему сечению напряжения одного знака. Такая область называется ядром сечения. Ядро сечения – область, расположенная вокруг центра тяжести сечения, приложенная внутри которой нагрузка, вызывает по всему поперечному сечению напряжения одного знака.
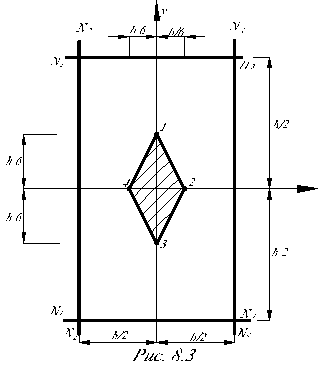
Для построения ядра сечения задаются положениями нейтральной линии, совпадающей со сторонами сечения Ni (хN и уN) и в соответствии с формулой (8.5) определяют две координаты точки приложения силы соответствующей этой линии
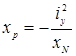
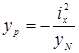 (8.7)
(8.7)
Проведя по всему контуру сечения нейтральные линии, получим n точек. На основании теоремы о вращении нейтральной линии, соединив последовательно полученные точки, получим ядро сечения (рис. 8.3). Для прямоугольного поперечного сечения ядром сечения является ромб.
Устойчивость сжатых стержней
Общие положения
Явление потери устойчивости сжатого стержня наблюдается в том случае, когда при известной форме и размерах поперечного сечения его длина превышает определенное значение.
При потере устойчивости элемента происходит нарушение первоначальной прямолинейной формы равновесия.
Различают устойчивое (а), безразличное (b) и не устойчивое (с) состояние равновесия (рис. 9.1).
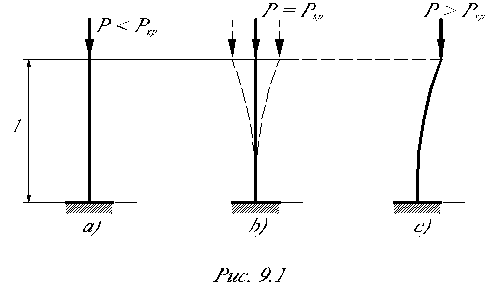 |
Продольный изгиб опасен тем, что происходит большое нарастание прогибов при малом росте сжимающей нагрузки.
Потеря устойчивости гибких стержней наступает при сравнительно небольших сжимающих напряжениях, которые с точки зрения прочности материала являются не опасными.
