Системы эконометрических уравнений

1. Наибольшее распространение в эконометрических исследованиях получили:

а) системы независимых уравнений;

б) системы рекурсивных уравнений;

в) системы взаимозависимых уравнений.

Ответ: в) системы взаимозависимых уравнений.

Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть системы.

2. Эндогенные переменные – это:

а) предопределенные переменные, влияющие на зависимые переменные, но не зависящие от них, обозначаются через .;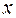

б) зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через ;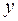

в) значения зависимых переменных за предшествующий период времени.

Ответ: б) зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через у.

Эндогенные переменные – это зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через .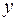

3. Экзогенные переменные – это:

а) предопределенные переменные, влияющие на зависимые переменные, но не зависящие от них, обозначаются через ;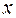

б) зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через ;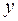

в) значения зависимых переменных за предшествующий период времени.

Ответ: а) предопределенные переменные, влияющие на зависимые переменные, но не зависящие от них, обозначаются через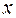

Экзогенные переменные – это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них. Обозначаются через .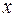

4. Лаговые переменные – это:

а) предопределенные переменные, влияющие на зависимые переменные, но не зависящие от них, обозначаются через .;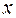

б) зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через ;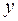

в) значения зависимых переменных за предшествующий период времени.

Ответ: в) значения зависимых переменных за предшествующий период времени

В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные).

5. Для определения параметров структурную форму модели необходимо преобразовать в:

а) приведенную форму модели;

б) рекурсивную форму модели;

в) независимую форму модели.

Ответ: а) приведенную форму модели

Для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

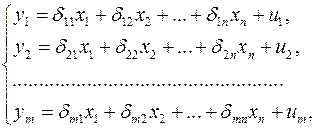
где 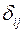– коэффициенты приведенной формы модели, 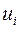– остаточная величина для приведенной формы.

6. Модель идентифицируема, если:

а) число приведенных коэффициентов меньше числа структурных коэффициентов;

б) если число приведенных коэффициентов больше числа структурных коэффициентов;

в) если число параметров структурной модели равно числу параметров приведенной формы модели.

Ответ: в) если число параметров структурной модели равно числу параметров приведенной формы модели.

Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.

7. Модель неидентифицируема, если:

а) число приведенных коэффициентов меньше числа структурных коэффициентов;

б) если число приведенных коэффициентов больше числа структурных коэффициентов;

в) если число параметров структурной модели равно числу параметров приведенной формы модели.

Ответ: а) число приведенных коэффициентов меньше числа структурных коэффициентов

Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.

8. Модель сверхидентифицируема, если:

а) число приведенных коэффициентов меньше числа структурных коэффициентов;

б) если число приведенных коэффициентов больше числа структурных коэффициентов;

в) если число параметров структурной модели равно числу параметров приведенной формы модели.

Ответ: б) если число приведенных коэффициентов больше числа структурных коэффициентов

Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров.

9. Уравнение идентифицируемо, если:

а) ;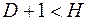

б) ;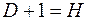

в) .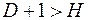

Ответ: б)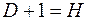

Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных (экзогенных) переменных (D), отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных (H) в данном уравнении без одного.

10. Уравнение неидентифицируемо, если:

а) ;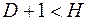

б) ;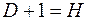

в) .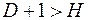

Ответ: а)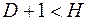

Уравнение неидентифицируемо, если выполняется неравенство .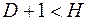

11. Уравнение сверхидентифицируемо, если:

а) ;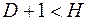

б) ;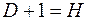

в) .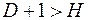

Ответ: в)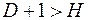

Уравнение сверхидентифицируемо, если выполняется неравенство .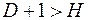

12. Для определения параметров точно идентифицируемой модели:

а) применяется двушаговый МНК;

б) применяется косвенный МНК;

б) ни один из существующих методов применить нельзя.

Ответ: б) применяется косвенный МНК

Косвенный метод наименьших квадратов (КМНК) применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы.

1. Структурная модель преобразовывается в приведенную форму модели.

2. Для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты .

3. Коэффициенты приведенной формы модели трансформируются в параметры структурной модели.

13. Для определения параметров сверхидентифицируемой модели:

а) применяется двушаговый МНК;

б) применяется косвенный МНК;

б) ни один из существующих методов применить нельзя.

Ответ: а) применяется двушаговый МНК;

Если система сверхидентифицируема, могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод наименьших квадратов (ДМНК).

Основная идея ДМНК – на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения.

14. Для определения параметров неидентифицируемой модели:

а) применяется двушаговый МНК;

б) применяется косвенный МНК;

б) ни один из существующих методов применить нельзя.

Ответ: б) ни один из существующих методов применить нельзя.

Модель неидентифицируема, если число параметров приведённой системы меньше чем, число параметров исходной модели, и в результате коэффициенты исходной модели не могут быть оценены через коэффициенты приведённой формы.

Временные ряды

1. Аддитивная модель временного ряда имеет вид:

а) ;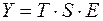

б) ;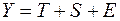

в) .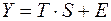

Ответ: б) ;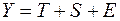

Общий вид аддитивной модели следующий:

.

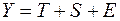Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой ( 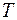), сезонной ( 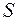) и случайной ( 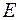) компонент.

2. Мультипликативная модель временного ряда имеет вид:

а) ;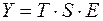

б) ;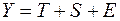

в) .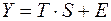

Ответ: а) ;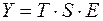

Общий вид мультипликативной модели выглядит так:

.

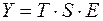Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой ( 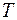), сезонной ( 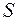) и случайной ( 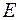) компонент.

3. Коэффициент автокорреляции:

а) характеризует тесноту линейной связи текущего и предыдущего уровней ряда;

б) характеризует тесноту нелинейной связи текущего и предыдущего уровней ряда;

в) характеризует наличие или отсутствие тенденции.

Ответ: а) характеризует тесноту линейной связи текущего и предыдущего уровней ряда.

Исходя из первого свойства коэффициента автокорреляции:

КЭ строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.

4. Аддитивная модель временного ряда строится, если:

а) значения сезонной компоненты предполагаются постоянными для различных циклов;

б) амплитуда сезонных колебаний возрастает или уменьшается;

в) отсутствует тенденция.

Ответ: а) значения сезонной компоненты предполагаются постоянными для различных циклов;

Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов.

5. Мультипликативная модель временного ряда строится, если:

а) значения сезонной компоненты предполагаются постоянными для различных циклов;

б) амплитуда сезонных колебаний возрастает или уменьшается;

в) отсутствует тенденция.

Ответ: б) амплитуда сезонных колебаний возрастает или уменьшается;

Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.

6. На основе поквартальных данных построена аддитивная модель временного ряда. Скорректированные значения сезонной компоненты за первые три квартала равны: 7 – I квартал, 9 – II квартал и –11 – III квартал. Значение сезонной компоненты за IV квартал есть:

а) 5;

б) –4;

в) –5.

7. На основе поквартальных данных построена мультипликативная модель временного ряда. Скорректированные значения сезонной компоненты за первые три квартала равны: 0,8 – I квартал, 1,2 – II квартал и 1,3 – III квартал. Значение сезонной компоненты за IV квартал есть:

а) 0,7;

б) 1,7;

в) 0,9.

8. Критерий Дарбина-Уотсона применяется для:

а) определения автокорреляции в остатках;

б) определения наличия сезонных колебаний;

в) для оценки существенности построенной модели.

Ответ: а) определения автокорреляции в остатках

Один из более распространенных методов определения автокорреляции в остатках – это расчет критерия Дарбина-Уотсона:

.

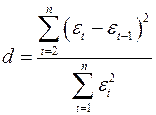Т.е. величина 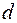есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.