Параметричне рівняння ліній

Нехай вектор 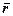в просторі задається своїми проекціями, які залежать від деякого параметра 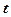, тобто

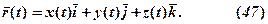
Очевидно, що (47) можна записати у вигляді

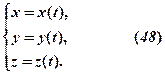
Якщо змінній 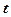надати певного значення 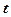= 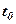, то за формулами (48) знайдемо відповідні значення 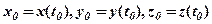. Множина точок 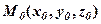може утворювати деяку лінію. Тому говорять, що рівняння (48) параметрично описують лінію.

Задача

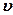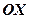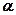1.З початку координат з швидкістю величиною , яка утворює з віссю кут , рухається точка під дією сили земного тяжіння. Знайти закон руху точки.

Розв’язання. Нехай вектор швидкості 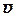, а його величина 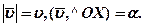(див. рис. 41).

Якщо б точка рухалась вільно, тільки з швидкістю 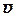, то за 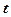секунд вона б перемістилась в положення 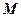. Але точка перебуває ще й під дією сили земного тяжіння, тому вона з положення 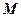опуститься в положення точки 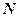і її ордината буде

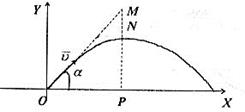
Рис. 41.

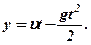
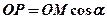Проекцією точки чи на ОХ є точка Р, тому або ж

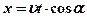. Отже, закон руху

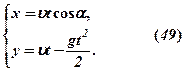
Якщо із системи (49) виключити 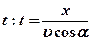, то

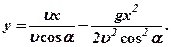
Як бачимо 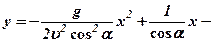парабола.

Розглянемо ще деякі приклади

Коло.

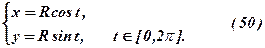
Із (50)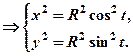

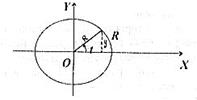
Рис. 42.

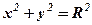– канонічне рівняння кола.

3. Еліпсможна записати у вигляді

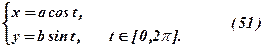
Із (51)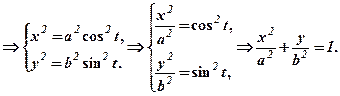

4. Циклоїда. – це траєкторія, яку описує фіксована точка кола, яке котиться вздовж прямої без ковзання.

Нехай 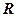радіус кола, а початкове положення фіксованної точки збігається з початком координат. При повороті на кут 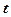ця точка зайняла положення точки 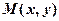(див. рис. 43).

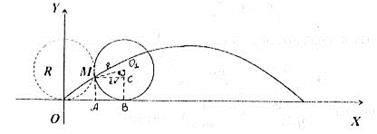
Рис. 43.

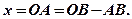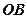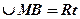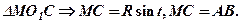Шлях , пройдений колом дорівнює довжині дуги . Із Отже

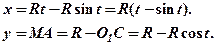Остаточно

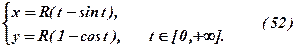
– параметричне рівняння циклоїди.

5. Гвинтова лінія– це траєкторія точки, яка рухається по циліндричній поверхні паралельно 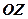рівномірно з швидкістю 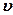, а циліндрична поверхня при цьому обертається з кутовою швидкістю 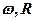– радіус циліндра (див. рис. 44). Позначимо через 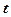час руху, тоді

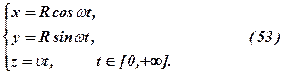
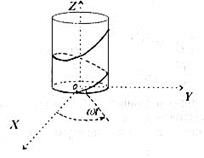
Рис. 44.