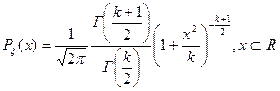Показательное (экспоненциальное) распределение
Широко используется в задачах теории массового обслуживания.
Непрерывная случайная величина  имеет показательное распределение с параметром
имеет показательное распределение с параметром 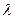 > 0, если она принимает только неотрицательные значения, а ее плотность распределения p
> 0, если она принимает только неотрицательные значения, а ее плотность распределения p  (x ) имеет соответственно вид:
(x ) имеет соответственно вид:
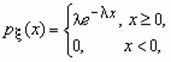
Нормальное распределение
Широко используется в статистических обследованиях, как эталонное распределение.
Случайная величина  нормально распределена с параметрами a и
нормально распределена с параметрами a и 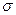 ,
, 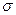 >0, если ее плотность распределения p
>0, если ее плотность распределения p  (x )
(x )
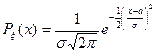
Гамма - распределение.
Широко используется в статистических обследованиях, как эталонное распределение.
Случайная величина  имеет Г-распределение (гамма-распределение) с параметрами a и b, если ее функция плотности вероятностей имеет вид:
имеет Г-распределение (гамма-распределение) с параметрами a и b, если ее функция плотности вероятностей имеет вид:
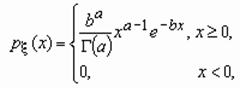 , a > 0, b > 0,
, a > 0, b > 0, 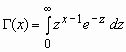
Бета-распределение.
Широко используется в статистических обследованиях, как эталонное распределение.
Случайная величина  имеет В-распределение (бета-распределение) с параметрами
имеет В-распределение (бета-распределение) с параметрами 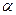 и
и 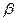 , если ее функция плотности вероятностей имеет вид:
, если ее функция плотности вероятностей имеет вид:
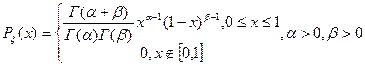
Распределение Коши.
Случайная величина  имеет распределение Коши с параметрами
имеет распределение Коши с параметрами 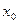 и
и 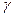 , если ее функция распределения имеет вид:
, если ее функция распределения имеет вид:
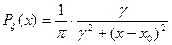
Распределение Лапласа.
Этот закон находит важные применения при статистических исследованиях.
Случайная величина  имеет распределение Лапласа (двустороннее экспоненциальное распределение) с параметром
имеет распределение Лапласа (двустороннее экспоненциальное распределение) с параметром 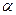 и
и 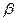 , если ее функция плотности вероятностей имеет вид:
, если ее функция плотности вероятностей имеет вид:
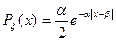
19. Распределение хи-квадрат ( 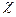 2- распределение)
2- распределение)
Этот закон находит важные применения при статистических исследованиях. По закону распределения c2 распределена так называемая статистическая дисперсия, т. е. статистическая оценка дисперсии.
Плотность вероятности этой случайной величины вычисляется по формуле:
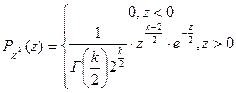
Здесь 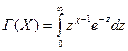 - гамма-функция Эйлера.
- гамма-функция Эйлера. 
20. Распределение хи ( 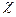 - распределение)
- распределение)
Плотность вероятности равна:
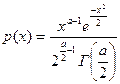 , x>0
, x>0
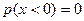
F-распределение ( распределение Снедекора).
Этот закон также находит важные применения при статистических исследованиях. По F-распределению распределено отношение статистических дисперсий сравниваемых величин.
Плотность вероятности этой случайной величины вычисляется по формуле:
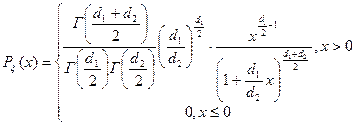
, где 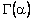 - гамма-функция.
- гамма-функция.
Распределение Стьюдента.
Этот закон также находит важные применения при статистических исследованиях(проверках). По закону распределения Стьюдента распределено отношение статистического математического ожидания к статистическому среднеквадратическому отклонению.
Плотность вероятности этой случайной величины вычисляется по формуле: