Обратная теорема. Углы с соответственно перпендикулярными сторонами равны между собой, если они оба острые или оба тупые.

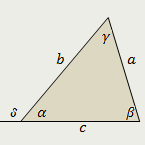
53.Углами (внутренними углами) треугольника называются три угла, каждый из которых образован тремя лучами, выходящими из вершин треугольника и проходящими через две другие вершины.

54. Теорема о сумме углов треугольника. Сумма углов треугольника равна 180°.

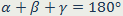
55. Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.

56. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.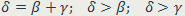

57. Если все три угла треугольника острые, то треугольник называется остроугольным.

58. Если один из углов треугольника тупой, то треугольник называется тупоугольным.

59. Если один из углов треугольника прямой, то треугольник называется прямоугольным.

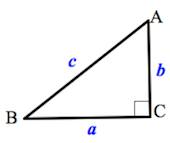
60. Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой (греч.слово gyipotenusa – «стягивающая»), а две стороны, образующие прямой угол — катетами (лат. слово katetos – «отвес»).

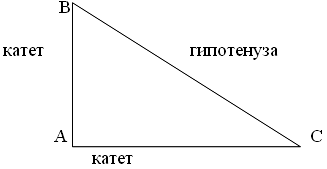
61. Теорема о соотношениях между сторонами и углами треугольника. В треугольнике против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.

62. В прямоугольном треугольнике гипотенуза больше катета.

т.к. напротив большего угла всегда лежит большая сторона.

Признаки равнобедреного треугольника.

- если в треугольнике два угла равны, то он равнобедренный;

- если в треугольнике биссектриса является медианой или высотой,
то этот треугольник равнобедренный;

- если в треугольнике медиана является биссектрисой или высотой, то

этот треугольник равнобедренный;

- если в треугольнике высота является медианой или биссектрисой,

то этот треугольник равнобедренный.

64. Теорема. Неравенство треугольника. Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон:

Свойство углов прямоугольного треугольника.

Сумма двух острых углов прямоугольного треугольника равна 90°.

A + В = 90°

66. Свойство прямоугольного треугольника.

Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.

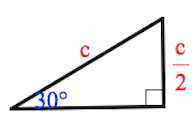
Если/ А = 30°, то ВС = ½ АВ

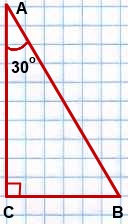
67.Свойства прямоугольного треугольника.

а) Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.

Если ВС = ½ АВ, то / B = 30°

Б) Медиана, проведенная к гипотенузе, равна половине гипотенузы.

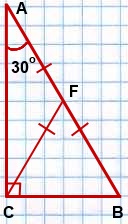медиана CF = ½ AB

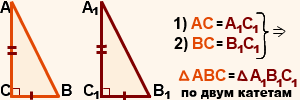
Признак равенства прямоугольных треугольников по двум катетам.

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.