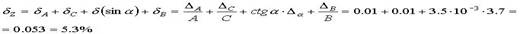Оценивание трансформированной систематической погрешности
Если погрешности ИК малы, то используют методы расчета, основанные на линеаризации. Если алгоритм 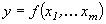 линейный, то при линеаризации получают точное выражение. Если обозначить
линейный, то при линеаризации получают точное выражение. Если обозначить 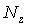 - код на входе ВК, а
- код на входе ВК, а 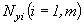 - выходной код i-го ИК,
- выходной код i-го ИК, 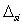 - систематическая погрешность i-го ИК, то для алгоритма
- систематическая погрешность i-го ИК, то для алгоритма
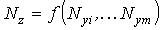
выражение трансформированной погрешности имеет вид:
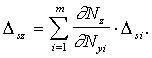 (1)
(1)
Если линеаризация невозможна, то используется формула полных приращений
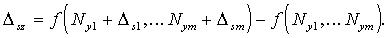 (2)
(2)
Если ИК содержит аддитивную погрешность, то в начальной части диапазона относительной погрешности могут оказаться значительными и там нужно использовать формулу полных приращений.
Формулы для вычисления трансформированной погрешности для часто встречающихся алгоритмов приведены в таблице 1, где
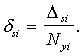
Таблица 1. Формулы для вычисления трансформированной систематической погрешности алгоритма.
 | Tрансформированная погрешность исходных данных |
| АЛГОРИТМ | Tочное выражение Выражение с использованием линеаризации |
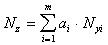  | 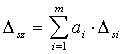 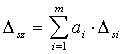 |
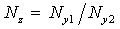  | 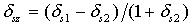 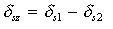 |
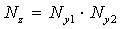 | 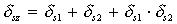 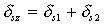 |
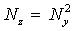 | 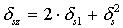 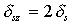 |
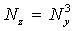 | 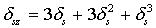 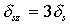 |
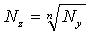 | 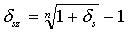 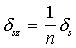 |
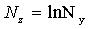 | 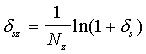 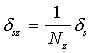 |
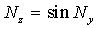 | 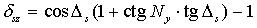 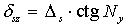 |
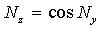 | 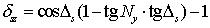 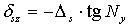 |
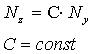 | 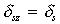 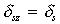 |
Пример 1. Вычислить трансформированную погрешность алгоритма
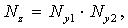
если 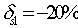 ,
, 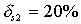
Решение
Т.к. погрешности большие, воспользуемся точным выражением
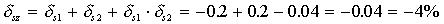
Выражение с использованием линеаризации неприменимо, т.к. тогда 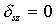
Пример 2. Оценить трансформированную погрешность алгоритма
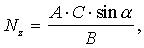
если заданы значения аргументов и систематические погрешности исходных данных:
А=10,0; С=20,0; В=10,0; =15,0; 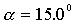 ;
; 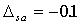 ;
; 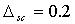 ;
; 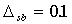 ;
; 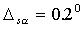
Решение
Т.к. погрешности малы, можно использовать линеаризацию. В соответствии с таблицей 1 получаем:
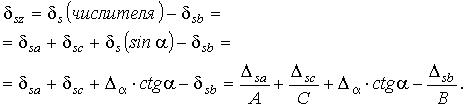
Подставляем значения абсолютных погрешностей и аргументов. Погрешность 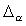 представляем в относительных единицах ( радианах). Получаем:
представляем в относительных единицах ( радианах). Получаем:
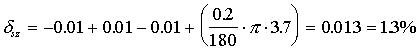
Пример 3. Таблицу 1 можно использовать для оценивания погрешности вычисления при представлении функций в виде таблиц. Пусть в алгоритме используется для вычислений таблица синусов в диапазоне от 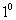 до
до 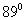 с дискретностью
с дискретностью 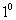 . Если при этоиспользовать алгоритм выбора ближайшего значения , то погрешность из-за дискретности
. Если при этоиспользовать алгоритм выбора ближайшего значения , то погрешность из-за дискретности 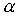 не превышает
не превышает 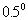 . Тогда погрешность вычисления синуса, т.е. алгоритма
. Тогда погрешность вычисления синуса, т.е. алгоритма 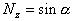 равна
равна
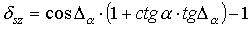 ( точное выражение )
( точное выражение )
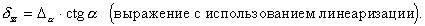
Рассчитаем погрешность вычисления функции 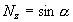 в двух точках диапазона для
в двух точках диапазона для 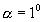
и 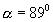 .
.
Решение
В этих двух случаях можно использовать приближенную формулу ,т.к. для 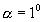 зависимость линейная, а для
зависимость линейная, а для 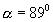
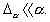 .
.
Тогда для 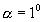
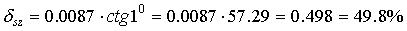 ;
;
для 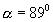
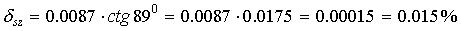 ;
;
1.2. Оценивание трансформированной случайной погрешности
При оценивании трансформированной случайной погрешности используют формулы, рассчитанные на линеаризацию, для некоррелированных погрешностей. Тогда для алгоритма 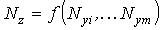
среднее квадратическое отклонение трансформированной погрешности равно
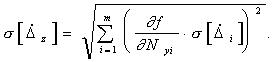 (3)
(3)
При необходимости рассчитывают смещение линеаризации
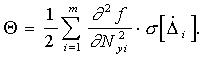 (4)
(4)
Формулы для вычисления трансформированной случайной погрешности для часто встречающихся алгоритмов приведены в таблице 2, где
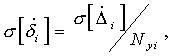
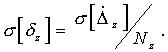
Таблица 2.Формулы для вычисления трансформированной случайной погрешности алгоритма.
| АЛГОРИТМ | Трансформированная погрешность исходных данных |
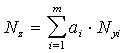 | 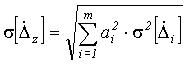 |
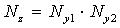 | 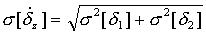 |
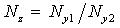 | 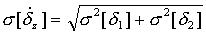 |
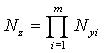 | 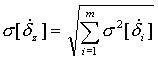 |
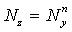 | 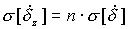 |
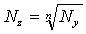 | 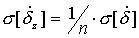 |
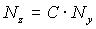 , C=const , C=const | 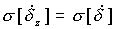 |
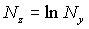 | 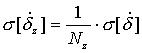 |
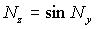 | 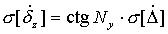 |
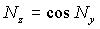 | 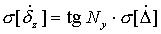 |
Пример 4. Для алгоритма 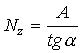 рассчитать СКО трансформированной случайной погрешности ,если А=1...10;
рассчитать СКО трансформированной случайной погрешности ,если А=1...10;
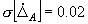 ;
; 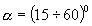 ;
; 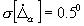 .
.
Решение
Выражение для погрешности  имеет вид
имеет вид
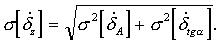
Для вычисления погрешности 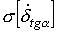 воспользуемся формулой (3)
воспользуемся формулой (3)
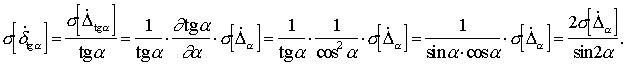
Нельзя представлять погрешность  через погрешности
через погрешности 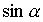 и
и 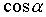 ,а затем использовать формулы из таблицы 2, т.к. погрешности
,а затем использовать формулы из таблицы 2, т.к. погрешности 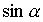 и
и 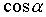 коррелированны, а таблица 2 рассчитана для независимых погрешностей.
коррелированны, а таблица 2 рассчитана для независимых погрешностей.
В итоге погрешность Nz представляется выражением
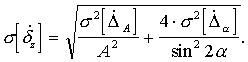

Т.к. погрешность 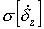 зависит от значений аргументов, необходимо оценить максимальную погрешность. Глобальный максимум будет соответствовать значениям А=1, и граничным значениям
зависит от значений аргументов, необходимо оценить максимальную погрешность. Глобальный максимум будет соответствовать значениям А=1, и граничным значениям 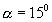 ;
; 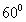 .
.
.
Найдем погрешность 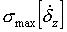 .
.
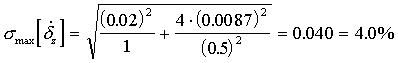
Пример 5. Для алгоритма 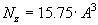
рассчитать СКО трансформированной случайной погрешности, если 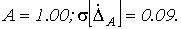
Оценить смещение линеаризации .
Решение
В соответствии с таблицей 2
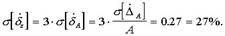
Тогда 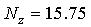
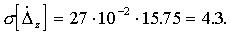
Таким образом, запись результата измерения в данном случае имеет вид Nz=16; Uc=4.
Оценим смещение линеаризации в соответствии с выражением (4).
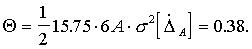
Значение  с учетом смещения линеаризации равно
с учетом смещения линеаризации равно
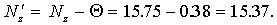
Тогда запись результата имеет вид: 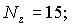
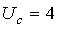 .
.
Таким образом можно сделать вывод о существенности нелинейности и целесообразности учета смещения линеаризации.
1.2. Оценивание трансформированной погрешности исходных данных, заданной в виде интервала
Если линеаризация невозможна, то для оценивания трансформированной погрешности используются правила интервального анализа. В этом случае аргументы представляют в виде границ интервала 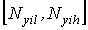 . Границы интервала отдельных операций находят в соответствии с правилами интервального анализа.
. Границы интервала отдельных операций находят в соответствии с правилами интервального анализа.
- Для сложения
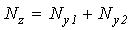 ;
;
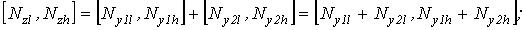 (5)
(5)
- Для вычитания
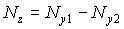 ;
;
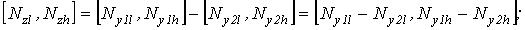 (6)
(6)
- Для умножения
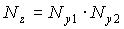 ;
;
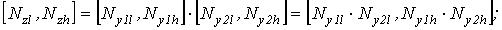 (7)
(7)
- Для деления
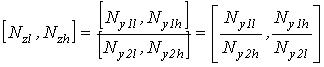 ; (8)
; (8)
После получения  в виде двух границ
в виде двух границ 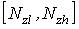 для записи результата с расширенной неопределенностью (Р=1)
для записи результата с расширенной неопределенностью (Р=1)
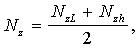 (9)
(9)
а границы неопределенности
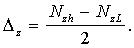 (10)
(10)
Тогда представление результата имеет вид: 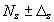
Для представления результата с комбинированной стандартной неопределенностью получают (при приписывании равномерного распределения)
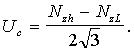 (11)
(11)
.
Тогда представление результата имеет вид:
 ;
; 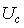
Пример 5. Найти трансформированную погрешность алгоритма 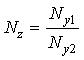 , если
, если 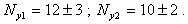
Записать результат с указанием неопределенности.
Решение
Для решения задачи представляем аргументы в виде границ 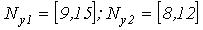 .
.
Тогда границы  равны (8)
равны (8)
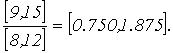
в соответствии с выражением (9) и (10) получаем 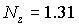 ;
; 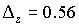 . Запись результата с расширенной неопределенностью
. Запись результата с расширенной неопределенностью
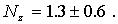
Запись результата с комбинированной стандартной неопределенностью (11) имеет вид
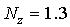 ;
; 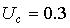 .
.
Если линеаризация возможна, то для оценивания трансформированной погрешности используются правила интервального анализа. В соответствии с этим выражение для границ трансформированной погрешности принимает вид
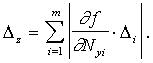 (12)
(12)
Если  представляет собой функцию одного аргумента , то для оценивания границ погрешности
представляет собой функцию одного аргумента , то для оценивания границ погрешности 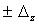 можно воспользоваться выражениями из таблицы 1. При наличии нескольких аргументов используют формулы таблицы 3.
можно воспользоваться выражениями из таблицы 1. При наличии нескольких аргументов используют формулы таблицы 3.
Таблица 3. Формулы для вычисления трансформированной погрешности алгоритма
(интервальный анализ с линеаризацией).
| Алгоритм | Трансформированная погрешность исходных данных |
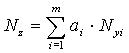 | 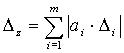 |
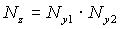 | 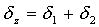 |
 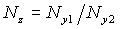 | 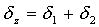 |
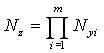 | 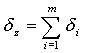 |
 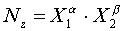 | 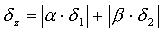 |
Пример 6. Оценить трансформированную погрешность алгоритма
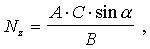
если заданы погрешности исходных данных в виде интервалов:
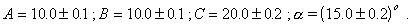
Решение
Т.к. погрешности малы, используем интервальный анализ с линеаризацией. Тогда