Геометричні фігури і операції над ними
Означення геометричних фігур.
Операції над геометричними фігурами
План
1. Точка, пряма,їх властивості.
2. Відрізок.
3. Кут.
4. Трикутник.
5. Коло, круг.
6. Многокутники.
7. Многогранники і тіла обертання.
Точка, пряма, їх властивості
Слово «точка» від латинського слова «punqo», що означає «доторкаюсь».
Слово «лінія» є перекладом від латинського слова «linea», що означає «льон», «льняна нитка», іноді це слово розуміють як «пряма лінія», і звідси походить слово «лінійка».
Точка– поняття, що не має означення. Уявлення про точку дає слід на аркуші паперу, зроблений добре загостреним олівцем, ручкою або крейдою на дошці.
•А  •В Позначаються точки великими латинськими
•В Позначаються точки великими латинськими
буквами: А,В,С...
 •С
•С
Пряма-поняття, що не визначається. Уявлення про пряму дають такі речі: туго натягнута нитка; промінь світла, який проходить крізь вузький отвір.
Позначається маленькою латинською літерою або двома великими латинськими буквами.
 а А • • В
а А • • В
Пряма нескінчена.
На малюнку точки і прямі наносяться добре загостреним олівцем. Для побудови прямих користуються лінійкою.
Властивості:
1.1. Через одну точку можна провести безліч прямих.


 •
•
1.2. Через будь – які дві точки можна провести пряму і тільки одну.
 А В а ۪ ۪
А В а ۪ ۪
1.3. Яка б не була пряма, існують точки , що належать цій прямій і точки, що не належать їй.
А •
а В
 •
•
В є а , А 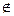 а.
а.
1.4. З трьох точок на прямій одна і тільки одна лежить між двома іншими.
 А • В • С •
А • В • С •
1.5. Дві різні прямі або перетинаються в одній точці, або не перетинаються.

Відрізок
Означення. Відрізок – частина прямої, обмежена двома точками, включаючи ці точки.

Відрізок позначається точками, що є його кінцями.
Позначення відрізка двома буквами, які відповідають його кінцям, запровадили ще стародавні греки.
 А• •В
А• •В
.
Рівні відрізки — відрізки, які співпадають при накладанні.
М
 А• • •В
А• • •В


 Середина відрізка – точка, яка ділить відрізок навпіл.
Середина відрізка – точка, яка ділить відрізок навпіл.
М – середина відрізка АВ, АМ = МВ.
Властивості:
2.1. Кожний відрізок має певну довжину, більшу від нуля.
 А • •
А • •  В
В
 а АВ = а, а > 0
а АВ = а, а > 0

Відстань між різними точками - довжина відрізка з кінцями в даних точках.
Відстань між точками, що співпадають,дорівнює 0.
2.4. Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою.
 А ۪ ۪ ۪ С АС = АВ + ВС
А ۪ ۪ ۪ С АС = АВ + ВС
В
2.5. Рівні відрізки мають рівні довжини. Якщо відрізки мають рівні довжини, то вони рівні.
2.6.Для будь-яких трьох точок відстань між двома з них не більша суми двох інших відстаней.
B
 А
А С А• B •
С А• B •  •C АС ≤ АВ + ВС
•C АС ≤ АВ + ВС
Кут
3.1. ПівпрямаА۪_________________
Означення: Частина прямої а, яка складається з усіх її точок, називається півпрямою або променем.
 |
Означеня кута
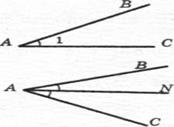
Кут — фігура, утворена двома променями, які виходять з однієї точки (вершини).
Кут позначають його вершиною або сторонами, або записують три точки: вершину і дві точки, що лежать на сторонах кута. Слово «кут» іноді замінюють знаком 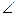
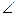 ВАС =
ВАС = 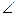 А =
А = 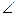 1
1
Рівні кути — кути, які співпадають при накладанні. 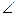 ВАN=
ВАN= 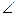 CAN
CAN
Одиниці вимірювання кутів:
Градус — величина (градусна міра) кута, яка дорівнює 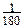 частині розгорнутого кута.
частині розгорнутого кута.
Хвилина - 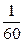 частина градуса.
частина градуса.
Секунда — 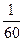 частина хвилини.
частина хвилини.
1° = 60´, 1´ = 60´´, 1´ = 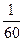 1°
1°
Властивості вимірювання кутів:
| 2.Кожний кут має певну градусну міру, більшу від нуля 3.Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами. 4. Від будь-якого променя в дану півплощину можна відкласти кут з даною градусною мірою, меншою за 180°, і тільки один. |
1. Якщо два кути мають рівні градусні міри, то вони рівні. Рівні кути мають рівні градусні міри
Види кутів
Кут називається розгорнутим, якщо його градусна міра дорівнює 1800.
Кут називається гострим, якщо його градусна міра менше, ніж 900.
 |
Кут називається прямим, якщо його градусна міра 900.
 |
Кут називається тупим, якщо його градусна міра більше 900, але менше 1800.

Бісектриса – промінь, який виходить із вершини кута й ділить його навпіл.
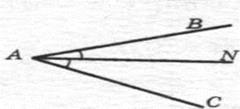
AN – бісектриса 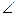 ВАС,
ВАС, 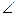 BAN =
BAN = 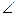 CAN
CAN
Трикутники
Означення: Трикутником називаєтьсяфігура, що складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, що сполучають ці точки попарно. Точки називаються вершинами, а відрізки – сторонами трикутника.
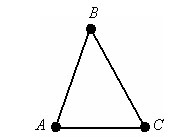
Вершини трикутника позначають великими латинськими літерами А, В, С, кути при відповідних вершинах грецькими літерами α, β, γ, а довжини протилежних сторін – маленькими латинськими літерами а, b, с.
Сума внутрішніх кутів трикутника – 180°. α+β+γ = 180°
Зовнішній кут трикутника (кут, суміжний до внутрішнього кута) завжди дорівнює сумі двох інших внутрішніх кутів трикутника.
Сума довжин двох будь-яких сторін трикутника завжди перевищує довжину третьої сторони. Це є нерівність трикутника або аксіома трикутника.
Трикутники можна класифікувати в залежності від відносної довжини його сторін:
· В рівносторонньому трикутнику всі сторони мають однакову довжину. Всі кути рівностороннього трикутника також рівні і дорівнюють 60°. Рівносторонній трикутник також називають правильним.
· В рівнобедреному трикутнику дві сторони мають однакову довжину, третя сторона при цьому називається основою трикутника. Рівнобедрений трикутник також має рівні кути, які знаходяться при його основі.
· Різносторонній трикутник має сторони різної довжини. Внутрішні кути різностороннього трикутника також різні.
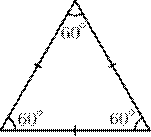 Рівносторонній Рівносторонній | 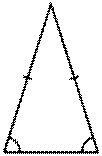 Рівнобедрений Рівнобедрений | 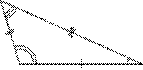 Різносторонній Різносторонній |
Також трикутники можна класифікувати відповідно до їх внутрішніх кутів:
· Прямокутний трикутник має один внутрішній кут рівний 90° (прямий кут). Сторона, протилежна до прямого кута, називається гіпотенузою. Інші дві сторони називаються катетами прямокутного трикутника.
· Тупокутний трикутник має один внутрішній кут більший, ніж 90°.
· В гострокутномутрикутнику всі кути менше за 90°. рівносторонній трикутник є гострокутним, але не всі гострокутні трикутники рівносторонні.
 Прямокутний Прямокутний | 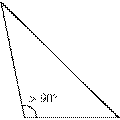 Тупокутний Тупокутний | 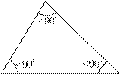 Гострокутний Гострокутний |
Коло, круг

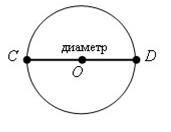
Коло — множина точок площини, відстань яких від даної точки (центра кола) дорівнює даній відстані (радіусу кола).
Радіус кола — відстань від центра кола до точки кола (відрізок, що з’єднує центр кола з точкою кола). ОD — радіус.
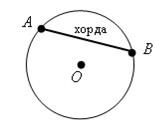
Хорда кола — відрізок, що з'єднує дві точки кола. AВ — хорда.
Діаметр кола — хорда, яка проходить через центр кола. CD - діаметр, CD = 2OD.
Круг — множина точок площини, відстань яких від даної точки (центра круга) не перевищує даної відстані (радіуса круга).
Радіус, хорда, діаметр кола, яке обмежує даний круг, називають радіусом круга, хордою круга, діаметром круга.
Многокутники
Чотирикутник – це частина площини, обмежена замкненою ламаною, яка містить чотири ланки. Вона складається з чотирьох вершин (точок) і чотирьох сторін (відрізків), що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій. Вершини називаються сусідніми, якщо вони є кінцями однієї з його сторін. Несусідні вершини називаються протилежними. Відрізки, що сполучають протилежні вершини чотирикутника, називаються діагоналями.
Сума кутів чотирикутника дорівнює 360°.  A +
A +  В +
В + 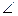 С +
С + 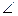 D = 360°.
D = 360°.
Кожна сторона чотирикутника менша за суму усіх його інших сторін.
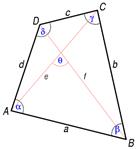 АВ < АD + ВС + СВ.
АВ < АD + ВС + СВ.
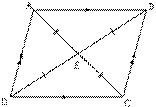 Паралелограм - це чотирикутник, протилежні сторони якого попарно паралельні.
Паралелограм - це чотирикутник, протилежні сторони якого попарно паралельні.
Існує декілька окремих видів паралелограмів:
Прямокутник – паралелограм, всі кути якого прямі;
Ромб – паралелограм, всі чотири сторони якого рівні;
Квадрат – рівносторонній прямокутник або прямокутний ромб.
Властивості паралелограма:
1. Протилежні сторони паралелограма рівні, тобто АВ = DC та AD = BC.
2. Протилежні кути паралелограма рівні, тобто 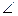 А =
А = 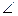 С та
С та 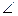 В =
В = 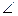 D.
D.
3. Діагоналі паралелограма перетинаються та в точці перетину діляться навпіл.
4. Сума сусідніх кутів дорівнює 1800, загальна сума кутів паралелограма дорівнює 3600.
5. Сума квадратів діагоналей дорівнює подвоєній сумі квадратів його сторін.
Властивості квадрата:
1. У квадрат завжди можна вписати коло.
2. Навколо квадрату завжди можна описати коло.
Властивості ромба:
1. Діагоналі ромба перетинаються під прямим кутом.
2. Діагоналі ромба є бісектрисами кутів, з яких вони проведені.