Основное определение дерева

Дерево - это специфический вид графов. Деревом называется связный граф, не содержащий циклов. Любой граф, не содержащий циклов, называется ациклическим, или лесом. Компонентами леса являются деревья.

Пример:

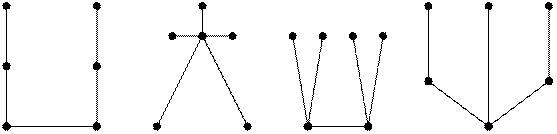ДРУГИЕ ОПРЕДЕЛЕНИЯ ДЕРЕВА

Теорема,дающая 5 различных определений дерева (теорема эквивалентности).

Для любого (p,q) - графа следующие утверждения эквивалентны:

1) граф G – дерево: связный ацикличный граф;

2) любые две несовпадающие вершины графа G соединены единственной простой цепью;

3) граф G связен и q=p-1(количество ребер в нем на 1 меньше, чем количество вершин);

4) граф G ацикличен и q=p-1;

5) граф G ацикличен и, если любую пару его несовпадающих несмежных вершин соединить ребром е, то полученный граф G+e будет содержать в точности один цикл.

Теорема о висячих вершинах дерева.

В любом нетривиальном ( 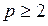) дереве имеются, по крайней мере, две висячие вершины.

Теорема о центральных вершинах дерева.

Центр любого дерева состоит либо из одной, либо из двух (смежных) вершин.

ЯРУСНАЯ ФОРМА ПРЕДСТАВЛЕНИЯ ДЕРЕВЬЕВ

Выберем некоторую произвольную фиксированную вершину дерева и назовем ее корнем. Будем полагать, что корень дерева расположен на 0 ярусе. Все остальные вершины сориентируем относительно корня следующим образом: на i-й ярус поместим вершины с расстоянием от корня, равным i. Концевые висячие вершины будем называть листами, а геодезические от корня к листу - ветвями.

СПОСОБЫ ОБХОДА ДЕРЕВЬЕВ

Существует два основных способа.

1. 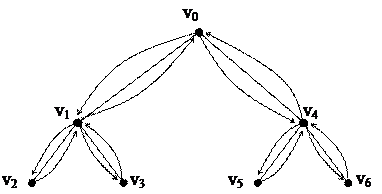Способ обхода (поиска) в глубину подразумевает просмотр ветвей в ярусном представлении дерева.

Начинаем поиск с некоторой фиксированной вершины v₀. Находим вершину u, смежную с v₀, и повторяем процесс, начиная с вершины u:

- если существует не просмотренная вершина, смежная с вершиной u, рассматриваем ее и, начиная с нее, продолжаем поиск;

- если не существует ни одной новой вершины, смежной с u, то говорят, что вершина u использована, и делается возврат в вершину, из которой мы попали в вершину u; продолжаем процесс;

- если на каком-то шаге u= v₀, и нет ни одной не просмотренной вершины, смежной v₀, то алгоритм заканчивает работу.

2. Способ обхода (поиска) в ширинуподразумевает просмотр вершин по ярусам с перебором вершин одного яруса.

ОСТОВЫ

Остов (каркас, скелет)графаG – это остовный подграф графа G, задающий дерево на каждой компоненте связности графа G.

Для связного графа остов – это дерево, покрывающее все вершины исходного графа.

Пусть есть некоторый граф G:

Очевидно, что в каждом графе существует остов, в общем случае, не один. Его можно получить, разрушая циклы в каждой компоненте связности.

Ребра остова Т некоторого графа G называются ветвями, а ребра графа G, не вошедшие в остов, называются хордами.

В первом остове графа G: (v₂,v₃), (v₃,v₄), (v₄,v₅) , (v₅,v₆) , (v₁,v₆) -ветви;

(v₁,v₂) , (v₂,v₆) , (v₂,v₅) , (v₃,v₆) , (v₃,v₅) -хорды.