Понятие и показатели силы связи в линейной регрессии

Сила связи характеризует, на сколько единиц в среднем изменится результат при изменении фактора на одну единицу.

- прямая связь. Сила связи больше, где больше ∆y.

∆ y Различают след. показатели силы связи:

1) абсол. показатель – коэф-т регрессии (изменение результата при изм-ии фактора на 1 ед.). Он хар-ет также направление связи (если b>0, то связь прямая, если b<0, то обратная).

Абсолютные пок-ли силы связи измеряются в тех же ед-х, что и изучаемые показ-ли. (руб,кг,шт..)

2) относительный показатель –коэф-т эластичности (изменение в среднем результата с изм-ем фактора на 1%). Это универсальный показатель силы связи, который рассчитывают для лин. и нелин. функций.

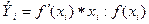
Например, для парной лин. регрессии y=a+bx+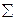

Э=b*(x/ a+bx). Он не является постоянной величиной (изм-ся х). обычно для усредненной характеристики Э по линейной функции берут х среднее.

3) относит. показатель – стандартизированный коэф-т регрессии (рассчитывается только для множественной регрессии). Стандартизация: t = y-y‾/ сигма y. Так как для станд. переменных альфа а=0, то ур-ие регрессии в станд. масштабе примет вид: y=в1 * tх1 + …+вp * txp +e. в=L * сигма х/сигма y, где L-коэф-т при х в исходной множ. регрессии.

При интерпретации коэф-та в ед. измерения – это сигма (ср. квадр. отклонение).

Относит. Показатели силы применяются,чтобы сравнивать факторы по силе (обеспечить сопоставимость влияния показателей фактора на рез-т, чего не могут абсол. Показ-ли, т.к. изменения м.б несоизмеримыми)

Можно сравнивать м\д собой коэф-т эластичности и стандартизир.показ-ли.

Вопрос №7. Понятие и показатели тесноты связи.

Вопрос №8. Особенности вычисления показателей тесноты связи парной линейной регрссии.

Когда мы изучаем тесноту связи, то мы смотрим, насколько близко реальные (фактические) значения расположены к линии регрессии (т.е. насколько близко точки к линии). Чем ближе, тем теснее.

На рис. 5 фактор лучше объясняет результат, чем на рис. 4. На рис. 4 скорее всего вмешивается еще какой-то фактор (а может и не один), который объясняет эту зависимость.

Поэтому если точки лежат близко, то выбираем функции вида: .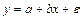

У 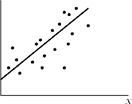Рис. 5: Невысокий показатель тес­ноты связи: большой разброс точек

А если далеко, то функции вида: 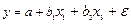Показатели тесноты связи показывает, насколько фактор или фак­торы, включенные в модель регрессии, объясняют изменение результата.

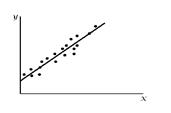Рис. 4: Высокий показатель тесно­ты связи: небольшой разброс точек

Показатели тесноты связи показывают насколько фактор или факторы, включенные в модель регрессии, объясняют изменение результата. Величина 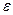характеризует тесноту связи (чем он меньше, тем связь тес­нее), с помощью метода наименьших квадратов мы оптимизировали эти отклонения. 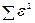характеризует разброс точек, тесноту связи.Эта величина является характеристикой связи, но ее нельзя использо­вать как показатель связи ввиду следующего недостатка: данная величина зависит от единиц измерения исходных показателей, если исходные показа­тели имеют разные единицы измерения, то тогда показатели будут несопо­ставимы.

Поэтому для того, чтобы получить показатель тесноты связи, приду­мали использовать правило сложения дисперсий. Это правило изучалось на лекциях по статистике для аналитической группировки, для линейной дисперсии это правило выглядит следующим образом:

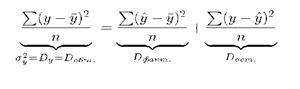
Можно сделать вывод о том, что деление на n можно опустить, тогда ничего не изменится:

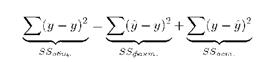
Где 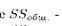общая сумма квадратов 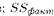. - факторная сумма квад­ратов: 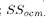- остаточная сумма квадратов. Основной недостаток суммы квадратов в его размерности, но оказыва­ется, что это часть от общей суммы:

Если 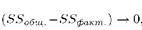, тогда связь максимально тесная. Ограничение такое, так как у нас часть целого:

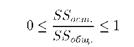Чем ближе к нулю, тем связь теснее, чем ближе к единице, тем связь слабее по этой формуле.

Можно, в принципе, использовать данное выражение как показатель тесноты связи, но удобнее, чтобы тесная связь была, когда ближе к 1. Поэтому рассмотрим другую формулу (которая и представляет собой показатель тесноты связи):

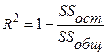
Если SS_ocm большая, то показатель стремится к нулю, и связь слабая.

Для линейных функций этот показатель называется коэффициентом детерминации, а если факторов много, то называется коэффициентом множественной детерминации.

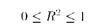
Из правил сложения дисперсий следует:

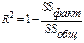
С ним есть функционально связанный показатель - коэффициент кор­реляции (или коэффициент множественной корреляции, если фак­торов много):

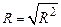
Для того, чтобы оценить, насколько тесна связь, используется шкала Чеддока (о силе связи судит, только по абсолютному значению 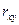, т.е берем по модулю, а, вообще, он может быть и отриц. и положит.):

0,1 – 0,3 - связь слабая

0,3 – 0,5 - связь умеренная

0,5 – 0,7 - связь заметная

0,7 – 0,9 - связь тесная

0,9 – 0,99 - связь очень тесная

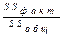Выводы по R: допустим, 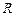=0,76 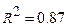, а значит, что связь между валовым доходом и среднегодовой стоимостью основных фондов и оборотных средств тесная. Выводы по 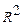делаются глядя на

- доля факторной дисперсии в общей дисперсии результата.

Следовательно, вариация валового дохода на 76% обусловлена вариацией факторов, включенных в модель регрессии, то есть вариацией среднегодовой стоимости основных фондов и оборотных средств.

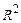- обычно для множ регрессии, а если парная линейная регрессия, то

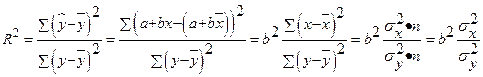
Эта формула действует хороша только для парной регрессии.

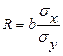
Следовательно: 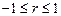. Если r=0,72, то связь тесная (смотрим на модуль) минус показывает, что связь обратная.