Принцип суперпозиции полей

Основная задача электростатики формулируется следующим образом: по заданному распределению в пространстве источников поля - электрических зарядов - найти значение вектора напряжённости 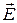во всех точках поля. Эта задача может быть решена на основе принципа суперпозиции электрических полей.

Напряжённость электрического поля системы зарядов равна геометрической сумме напряжённостей полей каждого из зарядов в отдельности.

Заряды могут быть распределены в пространстве либо дискретно, либо непрерывно. В первом случае напряжённость поля для системы точечных зарядов

,

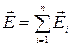где 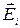- напряжённость поля i-го заряда системы в рассматриваемой точке пространства, n - общее число дискретных зарядов системы.

Если электрические заряды непрерывно распределены вдоль линии, то вводится линейная плотностьзарядов t, Кл/м.

t = (dq/dl),

где dq - заряд малого участка длиной dl.

Если электрические заряды непрерывно распределены по поверхности, то вводится поверхностная плотность зарядов s, Кл/м².

s = (dq/dS),

где dq - заряд, расположенный на малом участке поверхности площадью dS.

При непрерывном распределении зарядов в каком-либо объёме вводится объёмная плотность зарядов r, Кл/м³.

r = (dq/dV),

где dq - заряд, находящийся в малом элементе объёма dV.

Согласно принципу суперпозиции напряжённость электростатического поля, создаваемого в вакууме непрерывно распределёнными зарядами:

,

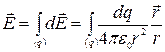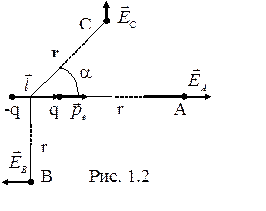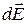где - напряжённость электростатического поля, создаваемого в вакууме малым зарядом dq, а интегрирование проводится по всем непрерывно распределённым зарядам.

Рассмотрим применение принципа суперпозиции к электрическому диполю.

Электрическим диполем называется система из двух равных по абсолютной величине и противоположных по знаку электрических зарядов (q и –q), расстояние l между которыми мало по сравнению с расстоянием до рассматриваемых точек поля. Вектор 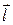, направленный по оси диполя от отрицательного заряда к положительному, называется плечом диполя. Вектор 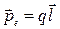называется электрическим моментом диполя (дипольным электрическим моментом). 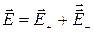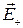Напряжённость поля диполя в произвольной точке ,где и 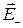- напряжённости полей зарядов q и -q (рис. 1.2).

В точке А, расположенной на оси диполя на расстоянии r от его центра (r>>l), напряжённость поля диполя в вакууме:

.

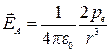В точке В, расположенной на перпендикуляре, восстановленном к оси диполя из его середины, на расстоянии r от центра (r>>l):

.

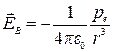В произвольной точке С модуль вектора напряженности

,

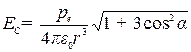где r - величина радиуса-вектора, проведенного от центра диполя к точке С; a - угол между радиусом-вектором 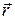и дипольным моментом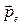(рис. 1.2).

1.3. Поток напряжённости. Теорема Гаусса для электростатического поля в вакууме

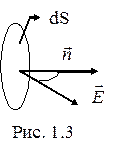Элементарным потоком напряжённости электрического полясквозь малый участок площадью dS поверхности, проведённой в поле, называется скалярная физическая величина

dN = 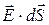= EdScos( 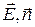) =E_ndS = EdS_^,

где 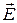— вектор напряжённости электрического поля на площадке dS, 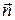- единичный вектор, нормальный к площадке dS, 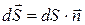-вектор площадки, Е_n = Ecos( 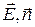) - проекция вектора 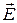на направление вектора 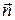, dS_^ = dScos( 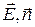) - площадь проекции элемента dS поверхности на плоскость, перпендикулярную вектору 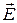(рис. 1.3).

Теорема Гаусса

Поток напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность пропорционален алгебраической сумме электрических зарядов, охватываемых этой поверхностью:

,

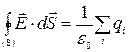где все векторы 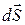направлены вдоль внешнихнормалей к замкнутой поверхности интегрирования S, которую часто называютгауссовой поверхностью.

1.4. Потенциал электростатического поля. Работа, совершаемая силами электростатического поля при перемещении в нём электрического заряда

Работа dА, совершаемая кулоновскими силами при малом перемещении 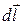точечного заряда q в электростатическом поле:

,

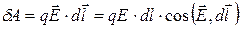где 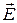- напряжённость поля в месте нахождения заряда q. Работа кулоновской силы при перемещении заряда q из точки 1 в точку 2 не зависит от формы траектории движения заряда (т.е. кулоновские силы являются консервативными силами). Работа сил электростатического поля при перемещении заряда q вдоль любого замкнутого контура L равна нулю. Это можно записать в виде теоремы о циркуляции вектора напряженности 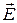электростатического поля.

Циркуляция вектора напряженности электростатического поля равна нулю:

.

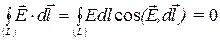Это соотношение, выражающее потенциальный характер электростатического поля, справедливо как в вакууме, так и в веществе.

Работа dА, совершаемая силами электростатического поля при малом перемещении точечного заряда q в электростатическом поле, равна убыли потенциальной энергии этого заряда в поле:

dА= - dW_П и А₁₂= - DW_П = W_П1 - W_П2,

где W_П1 и W_П2 - значения потенциальной энергии заряда q в точках 1 и 2 поля. Энергетической характеристикой электростатического поля служит его потенциал.

Потенциалом электростатического поля называется скалярная физическая величина j, равная потенциальной энергии W_П положительного единичного точечного заряда, помещённого в рассматриваемую точку поля, В.

.

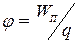Потенциал поля точечного заряда q в вакууме

.

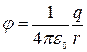Принцип суперпозиции для потенциала

,

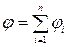т.е. при наложении электростатических полей их потенциалы складываются алгебраически.

Потенциал поля электрического диполя в точке С (рис. 1.2)

.

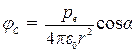Если заряды распределены в пространстве непрерывно, то потенциал j их поля в вакууме:

.

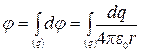Интегрирование проводится по всем зарядам, образующим рассматриваемую систему.

Работа А₁₂, совершаемая силами электростатического поля при перемещении точечного заряда q из точки 1 поля (потенциал j₁) в точку 2 (потенциал j₂):

А₁₂ = q (j₁ - j₂).

Если j₂ = 0, то .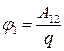

Потенциал какой-либо точки электростатического поля численно равен работе, совершаемой силами поля при перемещении положительного единичного заряда из данной точки в точку поля, где потенциал принят равным нулю.

При изучении электростатических полей в каких-либо точках важны разности, а не абсолютные значения потенциалов в этих точках. Поэтому выбор точки с нулевым потенциалом определяется только удобством решения данной задачи. Связь между потенциалом и напряжённостью имеет вид

Е_х = 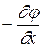, Е_у = 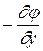, Е_z = 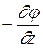и ,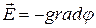

т.е. напряжённость электростатического поля равна по модулю и противоположна по направлению градиенту потенциала.

Геометрическое место точек электростатического поля, в которых значения потенциалов одинаковы, называется эквипотенциальной поверхностью. Если вектор 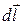направлен по касательной к эквипотенциальной поверхности, то 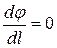и 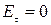. Это означает, что вектор напряженности перпендикулярен эквипотенциальной поверхности в каждой точке, т.е. E = E_n.

1.5. Примеры применения теоремы Гаусса к расчёту электростатических полей

Поле заряда q, равномерно распределённого по поверхности сферы радиусом R с поверхностной плотностью 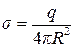выражается формулами:

если r > R, то 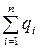= q и Е _r = .

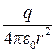если r < R, то 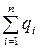= 0 и Е _r = 0.

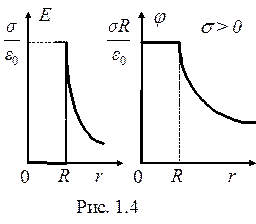Из связи между потенциалом и напряжённостью поля следует, что 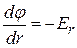. Полагая j =0 при r®¥ , получим для потенциала поля вне сферы (r³R):

.

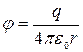Внутри сферы (r<R) потенциал всюду одинаков:

j = sR/e₀.

Графики зависимостей E _r и j от r приведены на рис. 1.4.

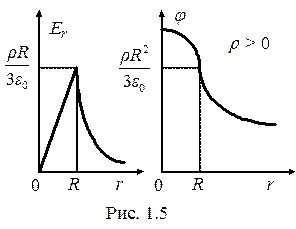Поле заряда q, равномерно распределённого в вакууме по объёму шара радиусом R с объёмной плотностью 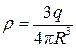выражается формулами:

если r>R, то 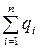= q и ;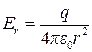

если r<R, то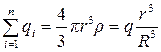

и .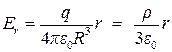

Из связи j и 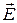следует, что для r>R ,

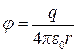для r<R j = j(R) - 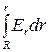и .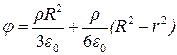

Графики зависимостей Е _r и j от r приведены на рис. 1.5.

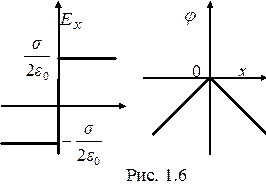Поле заряда, равномерно распределенного в вакууме по плоскости с поверхностной плотностью s.

Эта плоскость (х=0) является плоскостью симметрии поля, вектор напряжённости 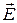которого направлен перпендикулярно плоскости от неё (если s>0) или к ней (если s < 0).

Для всех точек поля

.

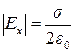Так как 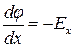, и полагая потенциал поля равным нулю в точках заряженной плоскости (х = 0), получим

.

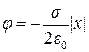Графики зависимостей Е и j от x приведены на рис. 1.6.