Исчисление высказываний и исчисление предикатов;

Исчисление высказываний, исчисление суждений, раздел математической логики, в котором формально-аксиоматическим методом изучаются сложные (составные) высказывания, составленные из простых (элементарных, не анализируемых) высказываний с помощью логических связок "и", "или", "если..., то" и "неверно, что". При этом ставится цель охарактеризовать общезначимые в том или ином смыслевысказывательные формы, т. е. те формулы, которые при любой подстановке высказываний вместо переменных дают высказывания, верные в соответствующем смысле.

Будем говорить, что ФАТ (формально-аксиоматическая теория) задана, если:

1. задан алфавит;

2. заданы формулы (слова в заданном алфавите);

3. определены аксиомы (выделенные формулы);

4.определены правила вывода 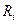(n-местное отношение на множестве формул Ф: ).

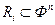Если формулы 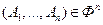,следовательно, 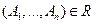, то формула есть непосредственное следствие из предыдущих формул по правилу .

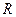Последовательность 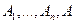— есть вывод формулы А, если любая формула А_i есть либо аксиома, непосредственное следствие предыдущих формул.

Пусть Г – множество формул.

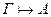, если 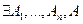, где любая из 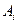- аксиома, -следствие, -либо формула из Г. Если 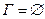, тогда 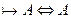– теорема.

Элементарные свойства выводимости.

Пусть 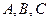– формулы, 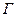– множество формул.

1. .

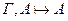2.Если 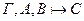, то .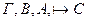

3.Если 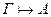, то .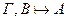

4.Если 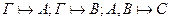, тогда .

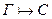5.Если 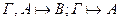, то .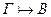

Исчисление высказываний:

1. Алфавит исчисления высказываний состоит из переменных высказываний: х,…, 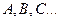, логических связок 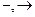и скобок .

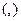1. Формулы:

а) все переменные являются формулами;

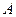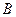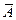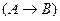б) если и – формулы, то и – формулы;

в) других нет.

3. Аксиомы.

I. ;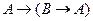

II. ;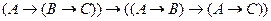

III. ;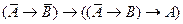

4. Правило вывода:

Modus Ponens. Есл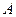и и 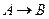– выводимые формулы, то 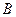выводима: .

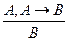Формула В есть непосредственное следствие формул А и .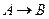

Предикатом Р( 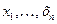) называется функция, переменные которой принимают значения из некоторого множества М, а само значение функции принимает значения: 1 или 0.

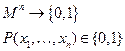
Предикат от n-переменных, называют n-местным предикатом.

Исчисление предикатов:

1) Алфавит:

1. Предметные переменные х₁, х₂…;

2. Предикатные константы а₁, а₂….;

3. Функциональные буквы 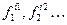, где i – количество аргументов;

4. Предикатные буквы ;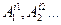

5. Логические связки ;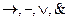

6. Кванторы существования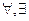

2) Формулы (слова в алфавите):

1. Термы.

1. предметные переменные и константы являются термами;

2. если fⁿ – функциональная буква, а t₁, … , t_n – термы, то fⁿ(t_{1, …} , t_n) – терм.

2. Формулы.

1. если Аⁿ – предикатная буква, а t_{1, … ,} t_n – термы, тогда Аⁿ (t₁,…, t_n) формула. Такая формула называется атомарной (элементарной). Все переменные в атомарной формуле являются свободными. Определение: переменная х является связанной, если х входит в квантор или находится в области действия квантора.

2. Если А формула, тогда 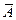- формула, причем все связанные переменные в А, являются связанными в .

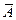3. Пусть А и В формулы, причем нет переменных которые были бы связаны в одной и свободны в другой, тогда 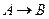- формула.

4. пусть А – формула и переменная х свободная, тогда 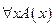и 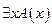- формулы.

3) Аксиомы:

1. А1, А2, А3

2. А4 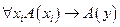, если А(х) не содержит переменной у;

3. А5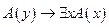

4) Правило вывода:

1. m.p.

2.

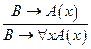
3. 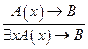, В не содержит х.

Под интерпретацией понимают систему М= 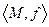, где М - непустое множество, а f – соответствие, сопоставляющего каждому предметному символу (букве) определенный предикат.

Формула называется общезначимой, если она принимает истинные значения на любом множестве

Теорема о полноте И Пр.

Ф-ла А выводима в И Пр Û когда она логически общезначима